算术逻辑单元(How Computes Calculate——The ALU)
一.前言
前面文章学习了逻辑门,那么一个个逻辑门是如果组合进行运算的呢?我们首先来了解计算机的运算基础单元——ALU,ALU就是一个个逻辑门组成的运算单元。
下图为第一个在单个芯片内的完整ALU,他是1970年发布的,这个芯片可以说是当时科技领域惊人的壮举,但是通过这一章的学习,我们来简做一个简单ALU电路,功能和因特尔74181一样。

二.“算术逻辑单元”(ALU)
如果想让两个数字完成相加运算,我们就要用“算术逻辑单元”(ALU)来处理,ALU就是计算机负责计算的组件,基本其他的组件也会用到它。
ALU有1个“算术单元”和一个“逻辑单元”组成
1.“算术单元”实现一个行波进位加法器
下面就通过一个例子来实现:ALU实现两个数字相加。
我们可以用一个个晶体管去拼,把这个电路做出来,但很快就会复杂的难以理解,所以我们为了便于理解,用更高层的抽象,之前学到的逻辑门来做,我们会用到AND,OR,NOT和XOR逻辑门
1.“半加器”
我们用二进制计算时会有四种情况(要理解下面的知识,你必须要先搞懂二进制)
1.0+0=0
2.1+0=1
3.0+1=1
4.1+1=10
我们会发现前三种情况输出和我们前面讲到的异或门XOR完全一致


至于1+1=10这种情况,我们也可以用小学数学学加法的一种思想:满十近一,只不过在二进制里,最大的个位数是1,所以要满二近一,所以1+1=10。

我们看异或门XOR只对了一部分,就是让1+1=0,但是没有记录近一位1,我们可以改进一下电路,加入一个AND门
如图:

我们可以用XOR门的输出记录当前位的运算值,用AND门口输出记录近位值,我们放大上面这张图,这个电路有个专门的名字——“半加器”
如图所示:
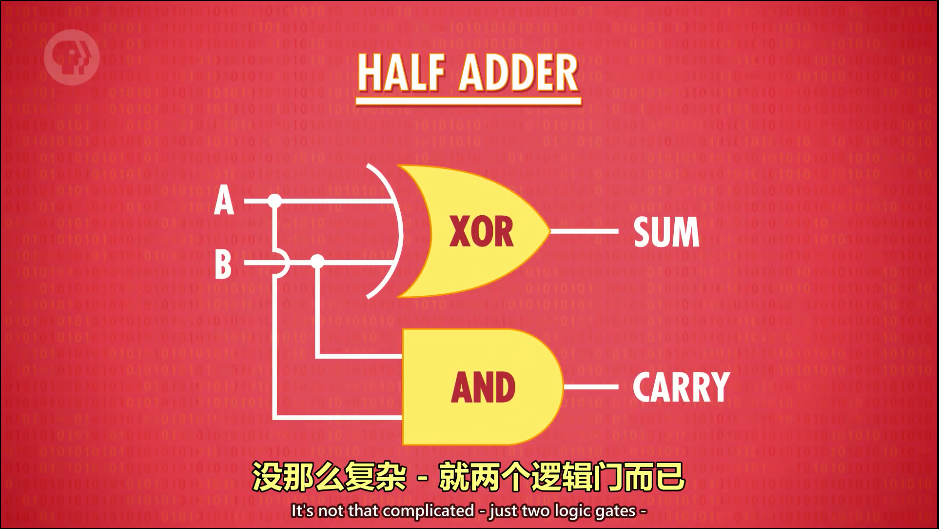
理解上面这两个这个“半加器”的输入输出后,为了便于理解,我们把这个半加器抽象为一个整体组件,如图:
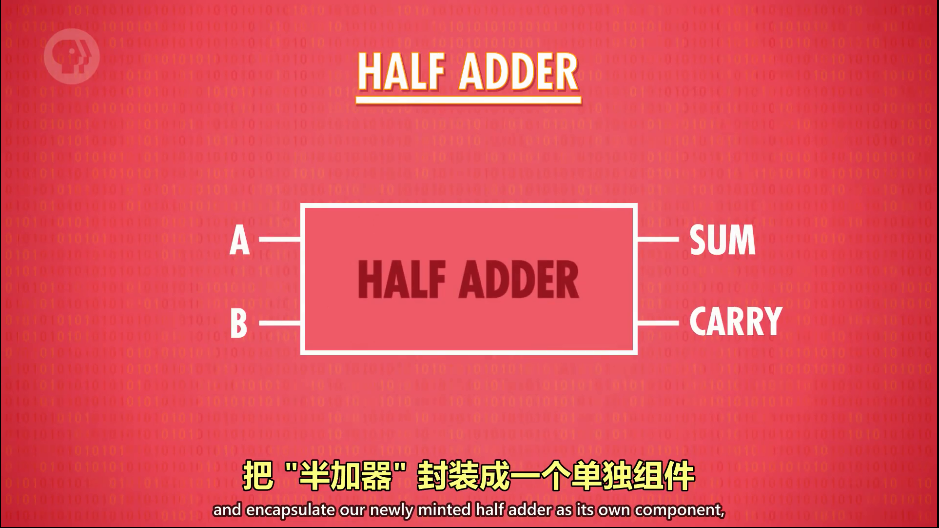
2.“全加器”
但是半加器其实只能处理“个位数”的运算,比如“111+111=1110”这个算式,如果我们只用满二加一的思想,会出现近一位后还要运算一加一,则会出现1+1+1的运算,这种运算情况我们需要在当前位写1,近位也要写1,很明显“半加器”已经无法满足这个运算,所以我们需要对半加器进行升级,升级后的组件叫“全加器”,如图为全加器算术表格:

我们可以用两个半加器加上一个OR门封装一个全加器组件,OR门的作用就是检查近位,如图:

全加器有三个输入,一个近位值,一个总和值。
了解完全加器和半加器之后,我们来用它们制做一个更加复杂的8位加法器,半加器可以完美的处理二进制的“个位运算”,所以可以将半加器作为8位加法器的个位运算组件,也就是8位数的第一位和第二位值的运算,然后将个位运算结果输入到下一个全加器,然后与8位数的第三位进行运算,运算的输出结果再输入到下一个全加器……以此类推到第8位的全加器
如图是一个完整的8位加法器组件连接:

我们观察最下面那个全加器的输出carry,如果第九位任然有近位,代表输入两个数字的和太大了,超过了8位加法器的运算范围,我们称之的“溢出”(overflow)
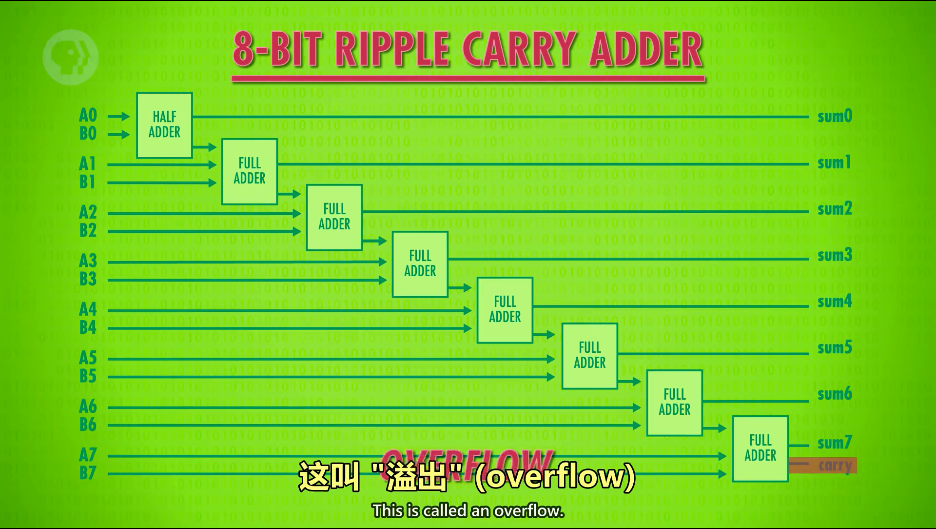
小时候玩吃豆子游戏就是一个8位溢出的最好例子,当我们通关第255关后,继续下一关游戏就会出现乱码,因为8位的最大值是十进制的255,因此256关会造成溢出bug,这个bug也成为了厉害吃豆人的代表
若果要避免溢出,我们可以加更多的全加器,以便于操作16位或者32位数字,让溢出更难发生,但代价是更多的逻辑门,另一个缺点是,每次近位都要一点时间,当然时间也不久,因为电子自动速度很快,但是对于如今的量级是每秒几十亿次运算,每一点时间都不容小觑的,所以现代计算机用的加法电路和我们上面说的有点不同,叫“超前近位加法器”,它更快,但做的事情也是一样的——二进制的相加
ALU的算术单元,还可以做如下数学运算,就像前面的加法器一样,这些操作也是由一些逻辑门构成的,我们只要简单了解就好了。

有趣的是,你可能会注意到上面的数学运算没有乘法和除法,那是因为简单的ALU没有专门的电路来处理乘除,而是把乘法多次加法来实现,你可能觉得这不是一种很好的设计,但是对于很多简单的处理器已经足够用了,同样也可以节约制作的成本,比如我们生活中用到的电视遥控器,微波炉,恒温器等等。

当然对于运算要求很高的设备如手机和电脑,它们的处理器,是有专门的乘除算术单元的。

你可能猜到了,乘法电路比加法复杂,不过也没有什么魔法,只是很多的逻辑门罢了,有兴趣的可以自行资料了解,这里就不做深入了。
2.“逻辑单元”
我们接下来讲ALU的另一半:“逻辑单元”
逻辑单元用来执行逻辑操作,比如之前讨论过的AND,OR,NOT操作都可以说是逻辑单元,它也能做简单的数值测试,比如逻辑单元可以检测一个数字是不是负数。
下面我们先来看一个“检查ALU输出是否为0”的电路,下面电路只有所有输入为0时才会输出1,这个电路我们后面文章会用到。

我们分析完上面电路后继续回到我们文章最开始提到的因“特尔74181”,“特尔74181”用了大概七十多个逻辑门,也不能进行乘除运算,而且只支持处理4位输出,比我们刚刚做的8位输出的ALU还低( ´͈ ᗨ `͈ ),不过我们做的没有人家完整,但是我们已经了解了完整的概念,如图为“特尔74181”的逻辑门:
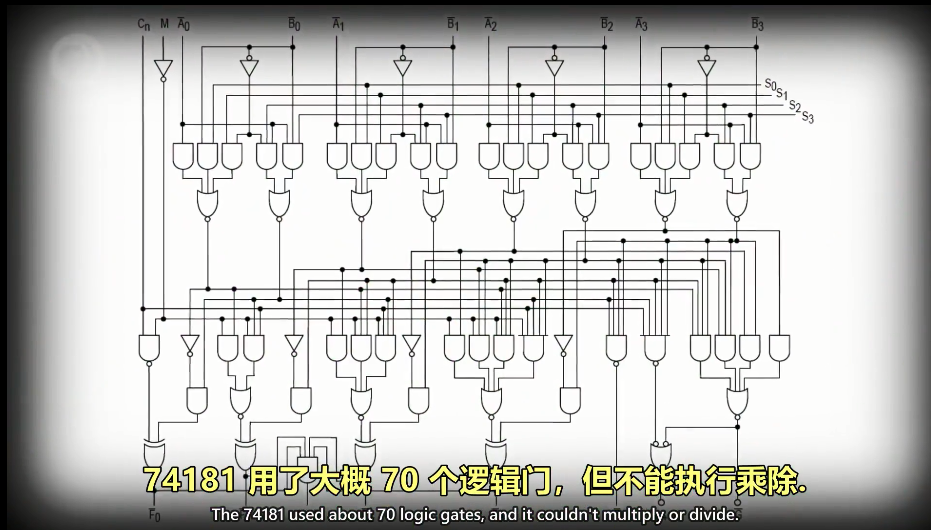
看这个4位的逻辑门就已经很复杂了,不用担心,我们不必要去想这些复杂的电路,我们把这个逻辑门也抽象位为一个整体组件
如图所示:
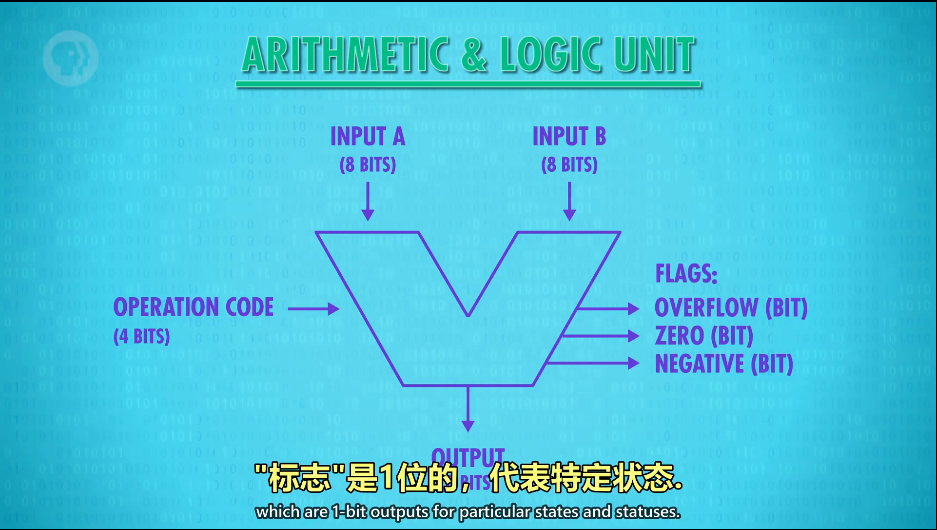
我们的8位ALU有两个输入(图上边两个),我们命名为输入A和B,都是8位(bits),我们还需要告诉ALU执行什么操作,所以我们加入一个组件来专门记录我们的操作代码(图左边),我们用4位记录操作代码,我们这里用“1000”代表加法命令代码,“1100”代表减法命令代码,操作代码会告诉ALU执行什么操作,我们还需要一个8位的输出(图下边),最后ALU还需要输出一堆标志(flag)(图右边三个标志,分别是输出是否溢出标志,输出是否为0标志,输出是否为负数标志),当然还可以有其他标志,我们目前只涉及这三个。
例如我们的ZERO标志判断输出是否为0,可以用来判断两个输入值是否相等,ZERO标志里面的逻辑就用到了我们前面提到的电路,如图所示:
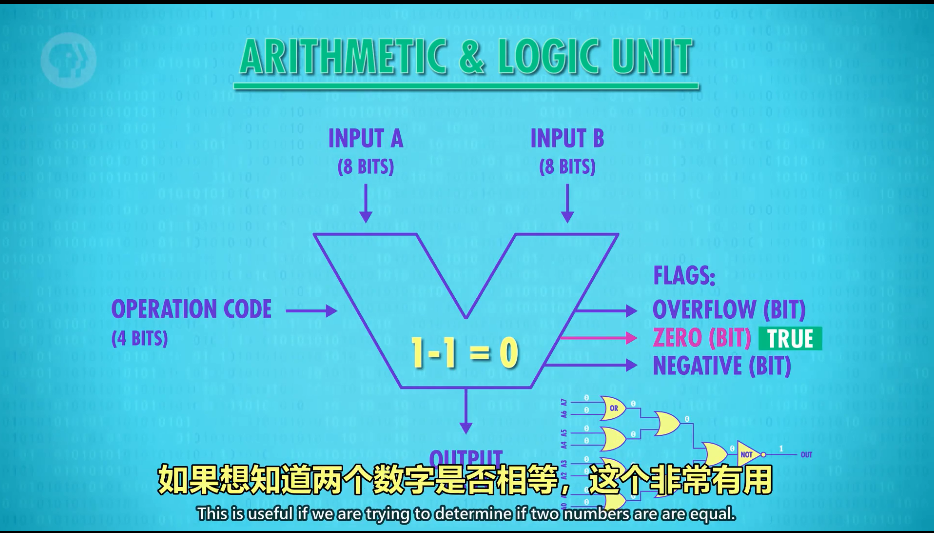
三.总结
我们现在知道了,计算机的最基础原件是如何进行运算的,后面两章,我们在学习完内存和寄存器之后,会用ALU做一个CPU,来整体了解计算机的运行过程。