归并排序(Merge Sort)
如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
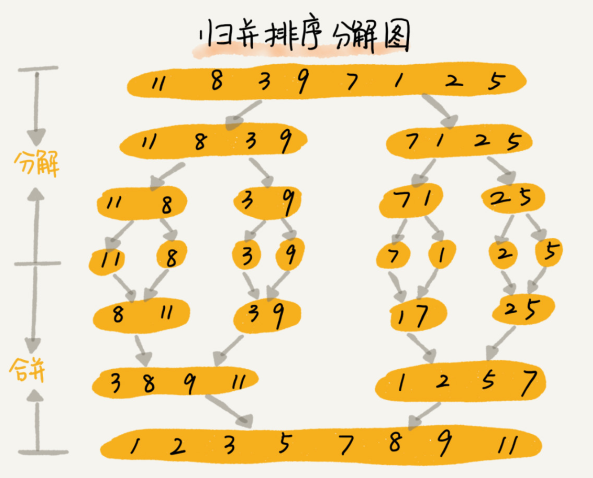
归并排序使用的就是分治思想。分治算法一般都是用递归来实现的。(分治是一种解决问题的处理思想,递归是一种编程技巧)
- 归并排序是一个稳定的排序算法。
- 归并排序的时间复杂度是非常稳定的,不管是最好情况、最坏情况,还是平均情况,时间复杂度都是 O(nlogn)。
- 但是,归并排序不是原地排序算法,归并排序的空间复杂度是 O(n)。(因为归并排序的合并函数,在合并两个有序数组为一个有序数组时,需要借助额外的存储空间)
<?php //递归调用,分解数组 function mergeSort(array $arr, $p, $r) { if ($p >= $r) { return [$arr[$r]]; } $q = (int)(($p + $r) / 2); $left = mergeSort($arr, $p, $q); $right = mergeSort($arr, $q + 1, $r); return merge($left, $right); } //合并 function merge(array $left, array $right) { $tmp = []; $i = 0; $j = 0; $leftLength = count($left); $rightLength = count($right); do { if ($left[$i] <= $right[$j]) { $tmp[] = $left[$i++]; } else { $tmp[] = $right[$j++]; } } while ($i < $leftLength && $j < $rightLength); $start = $i; $end = $leftLength; $copyArr = $left; if ($j < $rightLength) { $start = $j; $end = $rightLength; $copyArr = $right; } for (; $start < $end; $start++) { $tmp[] = $copyArr[$start]; } return $tmp; } $arr = [4, 5, 6, 1, 3, 2]; $length = count($arr); $p = 0; $r = $length - 1; $result = mergeSort($arr, $p, $r); print_r($result);
快速排序(Quicksort)
快排的思想是这样的:如果要排序数组中下标从 p 到 r 之间的一组数据,我们选择 p 到 r 之间的任意一个数据作为 pivot(分区点)。我们遍历 p 到 r 之间的数据,将小于 pivot 的放到左边,将大于 pivot 的放到右边,将 pivot放到中间。经过这一步骤之后,数组 p 到 r 之间的数据就被分成了三个部分,前面 p 到 q-1 之间都是小于 pivot 的,中间是 pivot,后面的 q+1 到 r 之间是大于 pivot 的。根据分治、递归的处理思想,我们可以用递归排序下标从 p 到 q-1 之间的数据和下标从 q+1 到r 之间的数据,直到区间缩小为 1,就说明所有的数据都有序了。
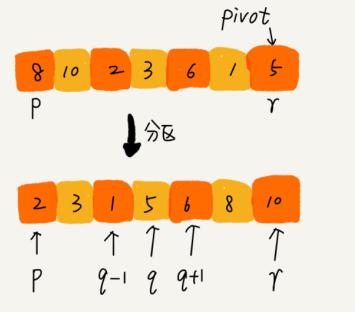
- 快排是一种原地、不稳定的排序算法。
- 快排的时间复杂度也是 O(nlogn)
归并排序和快速排序是两种稍微复杂的排序算法,它们用的都是分治的思想,代码都通过递归来实现,过程非常相似。归并排序算法是一种在任何情况下时间复杂度都比较稳定的排序算法,这也使它存在致命的缺点,即归并排序不是原地排序算法,空间复杂度比较高,是 O(n)。正因为此,它也没有快排应用广泛。
快速排序算法虽然最坏情况下的时间复杂度是 O(n ),但是平均情况下时间复杂度都是O(nlogn)。不仅如此,快速排序算法时间复杂度退化到 O(n ) 的概率非常小,我们可以通过合理地选择 pivot 来避免这种情况。
<?php function quickSort(array &$a) { $n = count($a); quickSortInternally($a, 0, $n - 1); } function quickSortInternally(array &$a, int $l, int $r) { if ($l >= $r) return; $q = partition($a, $l, $r); quickSortInternally($a, $l, $q - 1); quickSortInternally($a, $q + 1, $r); } function partition(&$a, $l, $r): int { $pivot = $a[$r]; $i = $l; for ($j = $l; $j < $r; ++$j) { if ($a[$j] < $pivot) { [$a[$j], $a[$i]] = [$a[$i], $a[$j]]; ++$i; } } [$a[$r], $a[$i]] = [$a[$i], $a[$r]]; return $i; } $a1 = [1, 4, 6, 2, 3, 5, 4]; $a2 = [2, 2, 2, 2]; $a3 = [4, 3, 2, 1]; $a4 = [5, -1, 9, 3, 7, 8, 3, -2, 9]; quickSort($a1); print_r($a1); quickSort($a2); print_r($a2); quickSort($a3); print_r($a3); quickSort($a4); print_r($a4);