https://ac.nowcoder.com/acm/problem/201895
题目
给一个2-SAT模板,构造一组数据,卡到$CNT>=frac{n^2}{2}$
#include<cstdio>
using namespace std;
const int N=3010;
int g[N<<1],nxt[N<<1],v[N<<1],num;
int q[N<<1],t;
bool vis[N<<1];
int CNT;
int n,m;
void add(int x,int y){
nxt[++num]=g[x];
v[num]=y;
g[x]=num;
}
bool dfs(int x){
CNT++;
if(vis[x>n?x-n:x+n])return 0;
if(vis[x])return 1;
vis[q[++t]=x]=1;
for(int i=g[x];i;i=nxt[i])if(!dfs(v[i]))return 0;
return 1;
}
bool solve(){
for(int i=1;i<=n;i++)if(!vis[i]&&!vis[i+n]){
t=0;
if(!dfs(i)){
while(t)vis[q[t--]]=0;
if(!dfs(i+n))return 0;
}
}
return 1;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y;scanf("%d%d",&x,&y);
if(x<0)x=n-x;if(y<0)y=n-y;
add(x>n?x-n:x+n,y);add(y>n?y-n:y+n,x);
}
solve();
return 0;
}
题解
当时根本不知道2-SAT是啥……
2-SAT是
有一些变量$a_1sim a_n$,给出一系列的形如$x lor y=1$,$x$和$y$是$a_i$或$!a_i$的方程,问是否存在一组解满足所有方程。
$x lor y=1$可以化为$( eg x o y)land( eg y o x)$
也就是如果一个点选择了,那么之后的点都要选择,当存在$a$和$ eg a$都选择的时候,就矛盾,这个模板就是用的爆搜
如果发现矛盾,就必须撤销选择,选择另外一个点,如果还是矛盾,肯定无解,如果不矛盾,就继续选择没有选择的点。
模拟这个过程,可以构造这样的图:
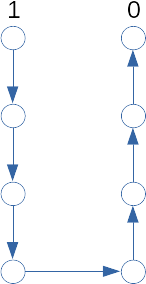
每次爆搜都要走到右边才会停止,大概就是搜索等差数列求和,$mathcal{O}(n^2)$次
最后变形为或的形式就可以了