逻辑回归
logistic regression
逻辑回归是线性的二分类模型
(与线性回归的区别:线性回归是回归问题,而逻辑回归是线性回归+激活函数sigmoid=分类问题)
模型表达式:
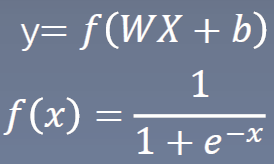
f(x)称为sigmoid函数,也称为logistic函数,能将所有值映射到[0,1]区间,恰好符合概率分布,如下图所示
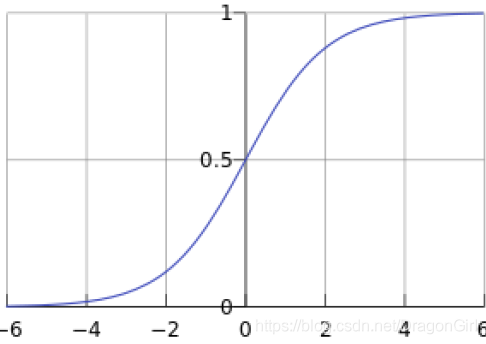
[0,1]区间形成二分类,一般以中点值(0.5)做界标,即
![]()
为什么说逻辑回归是线性的,是因为线性回归的wx+b与0的大小关系正好对应f(wx+b)中与0.5的大小关系,其实也可以用线性回归的大于或小于0来表示类别,但用sigmoid映射到概率区间更好体现置信度。
- 线性回归是分析自变量x与因变量y(标量)之间关系的方法
- 逻辑回归是分析自变量x与因变量y(概率)之间关系的方法
逻辑回归还有别名为对数几率回归
何为对数几率:
若将y视为样本x作为正例的可能性,则1-y为该样本作为负例的可能性。两者的比值y/1-y为“几率”,反映了x作为正例的相对可能性,取对数之后称为“对数几率”。
用y去拟合wx+b为线性回归,用对数几率去拟合wx+b即为对数几率回归。
对数几率回归与逻辑回归的等价性:

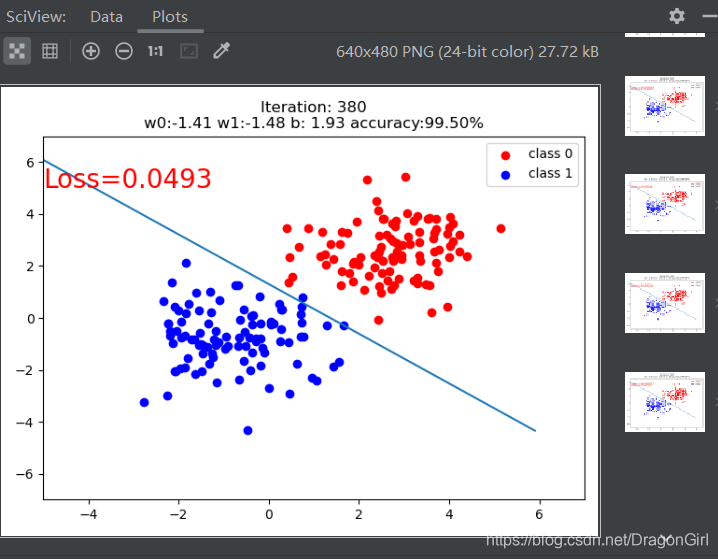
下面用代码实现二元逻辑回归模型。
(从这篇博文开始,所有构建模型的思路步骤都参照https://blog.csdn.net/DragonGirI/article/details/107396601这一推荐原则)
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
torch.manual_seed(10)
# ============================ step 1/5 生成数据 ============================
sample_nums = 100
mean_value = 1.7
bias = 1
n_data = torch.ones(sample_nums, 2)
x0 = torch.normal(mean_value * n_data, 1) + bias # 类别0 数据 shape=(100, 2)
y0 = torch.zeros(sample_nums) # 类别0 标签 shape=(100, 1)
x1 = torch.normal(-mean_value * n_data, 1) + bias # 类别1 数据 shape=(100, 2)
y1 = torch.ones(sample_nums) # 类别1 标签 shape=(100, 1)
train_x = torch.cat((x0, x1), 0)
train_y = torch.cat((y0, y1), 0)
# ============================ step 2/5 选择模型 ============================
class LR(nn.Module):
def __init__(self):
super(LR, self).__init__()
self.features = nn.Linear(2, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
x = self.features(x)
x = self.sigmoid(x)
return x
lr_net = LR() # 实例化逻辑回归模型
# ============================ step 3/5 选择损失函数 ============================
loss_fn = nn.BCELoss()
# ============================ step 4/5 选择优化器 ============================
lr = 0.01 # 学习率
optimizer = torch.optim.SGD(lr_net.parameters(), lr=lr, momentum=0.9)
# ============================ step 5/5 模型训练 ============================
for iteration in range(1000):
# 前向传播
y_pred = lr_net(train_x)
# 计算 loss
loss = loss_fn(y_pred.squeeze(), train_y)
# 反向传播
loss.backward()
# 更新参数
optimizer.step()
# 清空梯度
optimizer.zero_grad()
# 绘图
if iteration % 20 == 0:
mask = y_pred.ge(0.5).float().squeeze() # 以0.5为阈值进行分类
correct = (mask == train_y).sum() # 计算正确预测的样本个数
acc = correct.item() / train_y.size(0) # 计算分类准确率
plt.scatter(x0.data.numpy()[:, 0], x0.data.numpy()[:, 1], c='r', label='class 0')
plt.scatter(x1.data.numpy()[:, 0], x1.data.numpy()[:, 1], c='b', label='class 1')
w0, w1 = lr_net.features.weight[0]
w0, w1 = float(w0.item()), float(w1.item())
plot_b = float(lr_net.features.bias[0].item())
plot_x = np.arange(-6, 6, 0.1)
plot_y = (-w0 * plot_x - plot_b) / w1
plt.xlim(-5, 7)
plt.ylim(-7, 7)
plt.plot(plot_x, plot_y)
plt.text(-5, 5, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color': 'red'})
plt.title("Iteration: {}\nw0:{:.2f} w1:{:.2f} b: {:.2f} accuracy:{:.2%}".format(iteration, w0, w1, plot_b, acc))
plt.legend()
plt.show()
plt.pause(0.5)
if acc > 0.99:
break运行结果