前言
之前已经提到过好几次Attention的应用,但还未对Attention机制进行系统的介绍,这里对attention机制做一个概述,免得之后看阅读理解论文的时候被花式Attention弄的晕头转向。
Seq2Seq
注意力机制(Attention Mechanism)首先是用于解决 Sequence to Sequence 问题提出的,因此我们了解下研究者是怎样设计出Attention机制的。
Seq2Seq,即序列到序列,指的是用Encoder-Decoder框架来实现的端到端的模型,最初用来实现英语-法语翻译。Encoder-Decoder框架是一种十分通用的模型框架,其抽象结构如下图所示:

其中,Encoder和Decoder具体使用什么模型都是由研究者自己定的,CNN/RNN/Transformer均可。Encoder的作用就是将输入序列映射成一个固定长度的上下文向量C,而Decoder则将上下文向量C作为预测(Y_1)输出的初始向量,之后将其作为背景向量,并结合上一个时间步的输出来对下一个时间步进行预测。
由于Encoder-Decoder模型在编码和解码阶段始终由一个不变的语义向量C来联系着,这也造成了如下一些问题:
- 所有的输入单词 X 对生成的所有目标单词 Y 的影响力是相同的
- 编码器要将整个序列的信息压缩进一个固定长度的向量中去,使得语义向量无法完全表示整个序列的信息
- 最开始输入的序列容易被后输入的序列给覆盖掉,会丢失许多细节信息,这点在长序列上表现的尤为明显
Attention机制的引入
Attention机制的作用就是为模型增添了注意力功能,使其倾向于根据需要来选择句子中更重要的部分。
加入加入Attention机制的Seq2Seq模型框架如下图所示:
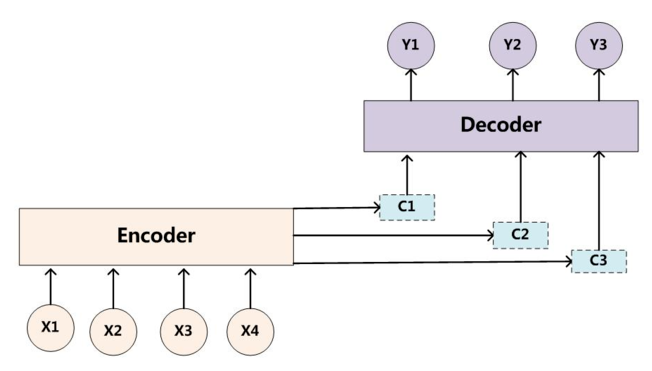
与传统的语义向量C不同的是,带有注意力机制的Seq2Seq模型与传统Seq2Seq模型的区别如下:
- 其为每一次预测都有不同的上下文信息(C_i)
其中(s_i)表示Decoder上一时刻的输出状态,(c_i)为当前的时刻的中间语义向量
- 当前的时刻的中间语义向量(c_i)为对输入信息注意力加权求和之后得到的向量,即:
其中(h_j)为Encoder端的第j个词的隐向量,(alpha_{ij})表示Decoder端的第i个词对Encoder端的第j个词的注意力大小,即输入的第j个词对生成的第i个词的影响程度。这意味着在生成每个单词(Y_i)的时候,原先都是相同的中间语义表示(C)会替换成根据当前生成单词而不断变化的(c_i)。生成(c_i)最关键的部分就是注意力权重(alpha_{ij})的计算,具体的计算方法我们下面再讨论。
Hard or Soft
之前我们提到的为Soft Attention的一般形式,还有一种Hard Attention,其与Soft Attention的区别在于,其通过随机采样或最大采样的方式来选取特征信息(Soft Attention是通过加权求和的方式),这使得其无法使用反向传播算法进行训练。因此我们常用的通常是Soft Attention
Global or Local
Global Attention 与 Local Attention 的区别在于二者的关注范围不同。Global Attention 关注的是整个序列的输入信息,相对来说需要更大的计算量。而 Local Attention 仅仅关注限定窗口范围内的序列信息,但窗口的限定使得中心词容易忽视不在窗口范围内的信息,因此窗口的大小设定十分重要。在实践中,默认使用的是Global Attention。
注意力的计算
我们之前已经讨论过,中间语义向量(c_i)为对输入信息注意力加权求和之后得到的向量,即:
而注意力权重(alpha_{ij})表示Decoder端的第i个词对Encoder端的第j个词的注意力大小,即输入的第j个词对生成的第i个词的影响程度。其基本的计算方式如下:
其中,(s_{i-1})需要根据具体任务进行选择,对于机器翻译等生成任务,可以选取 Decoder 上一个时刻的隐藏层输出,对于阅读理解等问答任务,可以选择问题或问题+选项的表征,对于文本分类任务,可以是自行初始化的上下文向量。而(h_j)为 Encoder 端第j个词的隐向量,分析上面公式,可以将Attention的计算过程总结为3个步骤:
-
将上一时刻Decoder的输出与当前时刻Encoder的隐藏词表征进行评分,来获得目标单词 Yi 和每个输入单词对应的对齐可能性(即一个对齐模型),Score(·)为一个评分函数,一般可以总结为两类:
- 点积/放缩点积:
[e_{ij} = Score(s_{i-1}, h_j) = s_{i-1} cdot h_j ][e_{ij} = Score(s_{i-1}, h_j) = frac{s_{i-1} cdot h_j}{||s_{i-1}||cdot||h_j||} ]- MLP网络:
[e_{ij} = Score(s_{i-1}, h_j) = MLP(s_{i-1}, h_j) ][e_{ij} = Score(s_{i-1}, h_j) = s_{i-1}Wh_{j} ][e_{ij} = Score(s_{i-1}, h_j) = W|h_j;s_{i-1}| ] -
得到对齐分数之后,用Softmx函数将其进行归一化,得到注意力权重
-
最后将注意力权重与 Encoder 的输出进行加权求和,得到需要的中间语义向量(c_i)
将公式整合一下:
其中,(Query)为我们之前提到的(s_{i-1}),(Keys) 和 (Values)为 (h)
Self-Attention
重温一下我们讲解Transformer时提到的Self-Attention,其 (Query),(Keys) 和 (Values) 均为Encoder层的词表征通过一个简单的线性映射矩阵得到的,即可将其表示为
从其注意力分数的计算方法上来看也是一种典型的缩放点积,其关键在于仅对句子本身进行注意力权值计算,使其更能够把握句子中词与词之前的关系,从而提取出句子中的句法特征或语义特征。

小结
这一块对Attention的基本原理进行了一个简单的总结,主要是对自己只是的巩固,以及对之后的实践工作做铺垫,之后有时间再将Attention这块相关的代码写出来。
参考链接
https://zhuanlan.zhihu.com/p/31547842
https://zhuanlan.zhihu.com/p/59698165
https://zhuanlan.zhihu.com/p/53682800
https://zhuanlan.zhihu.com/p/43493999