K-means的缺点
昨天记录了使用K-means对网格模型进行分割的步骤和一些简单的结果,从昨天的实验结果来看,使用顶点坐标和顶点法向作为K-means聚类的特征得到的分割效果总体上还是不错的。分割结束后,每个顶点会被赋予一个分割的标号。
但是,只使用顶点距离作为聚类得到的结果并没有语义,因此可能会得到一些不太好的聚类结果。
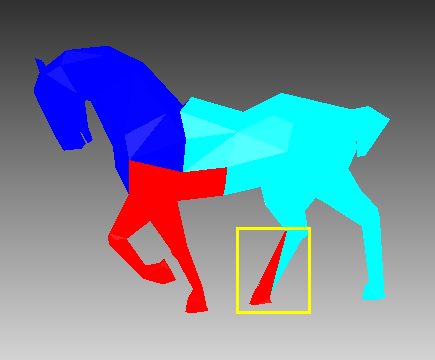
如上图所示,“马”模型的右后腿和两条左腿被分割到了同一个类,这使得分割的结果不具有连通性,因此在后续的学习中,需要对该算法的分割结果进行调整,或者需找更加合适的分割方法。
分割边界的获取
边界获取的思想挺简单,首先遍历网格顶点,筛选出某一特定区域的顶点,对于这一区域中某一顶点,判断其一邻域中的顶点的标号与其自身标号是否相同,如果存在不同标号与自身标号不同的顶点,那么这样的顶点就是边界顶点。找出边界顶点后,为其设置边界标记。同时,记录区域中非边界顶点的个数,以便于计算区域局部的拉普拉斯矩阵。
寻找边界代码如下
void find_Boundary(PolygonMesh::Mesh * _mesh, int area)
{
/*_mesh: 输入的网格
area: 区域编号
*/
num_vtx = _mesh->n_vertices();
is_boundray.clear();
for ( int i = 0; i < num_vtx; i++ )
{
//默认所有顶点都不是边界当某个顶点的1领域中有一个顶点标号和它不同时,这个顶点为边界顶点
is_boundray.push_back(0);
}
int v_idx = 0;
cnt_non_bdy = 0;//非边界顶点个数
for (auto v_it = _mesh->vertices_begin();v_it != _mesh->vertices_end();++v_it,v_idx++)
{
if (all_lables[v_idx] == area)
{
for ( auto vv_it = _mesh->vv_begin(v_it); vv_it != _mesh->vv_end(v_it); ++vv_it)
{
OpenMesh::VertexHandle vertex2 = vv_it.handle();
int v2_idx = vertex2.idx();
//当某个顶点的1领域中有一个顶点标号和它不同时,这个顶点为边界顶点
if ( all_lables[v2_idx] !=area )
{
is_boundray[v_idx]=1;
break;
}
}
}
//区域area中的非边界顶点
if (all_lables[v_idx] == area && is_boundray[v_idx] !=area )
{
cnt_non_bdy++;
}
}
}
需要注意的是,在计算区域的拉普拉斯矩阵时,如果使用L = D - A这种形式的拉普拉斯矩阵,在计算顶点度矩阵和顶点邻接矩阵A时,都要将其邻域中的边界迪昂点排除在外
计算度矩阵和邻接矩阵代码
int v_idx = 0;
int n_vidx = 0;//对同一区域中的顶点重新编号
VectorX byd_neibor;//记录每个顶点的边界邻域
byd_neibor.setZero(cnt_non_bdy);
for(auto v_it = _mesh->vertices_begin();v_it != _mesh->vertices_end();++v_it,++v_idx)
{
if (all_lables[v_idx] == 1 && is_boundray[v_idx] !=1 )
{
//计算其边界点邻居个数
for ( auto vv_it = _mesh->vv_begin(v_it); vv_it != _mesh->vv_end(v_it); ++vv_it)
{
OpenMesh::VertexHandle vertex2 = vv_it.handle();
int v2_idx = vertex2.idx();
//当某个顶点的1领域中有一个顶点标号和它不同时,这个顶点为边界顶点
if ( all_lables[v2_idx] !=1 )
{
byd_neibor[n_vidx]++;
}
}
//获得顶点i的度,然后减去边界点个数
int val = _mesh->valence(v_it.handle());
D_matrix(n_vidx ,n_vidx ) = val - byd_neibor[n_vidx];
//获得顶点的1邻域邻接矩阵
OpenMesh::VertexHandle vertex1 = v_it.handle();
int v1_idx = vertex1.idx();
for ( auto vv_it = _mesh->vv_begin(v_it); vv_it != _mesh->vv_end(v_it); ++vv_it)
{
OpenMesh::VertexHandle vertex2 = vv_it.handle();
int v2_idx = vertex2.idx();
if (is_boundray[v2_idx] != 1)//筛选非边界的邻居顶点
{
A_matrix(n_vidx,n_vidx) = 1;
}
}
n_vidx ++;//对同一区域中的顶点进行新的编号
}
}