Problem Description
Let's play a card game called Gap.
You have 28 cards labeled with two-digit numbers. The first digit (from 1 to 4) represents the suit of the card, and the second digit (from 1 to 7) represents the value of the card.
First, you shu2e the cards and lay them face up on the table in four rows of seven cards, leaving a space of one card at the extreme left of each row. The following shows an example of initial layout.
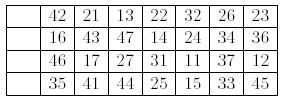
Next, you remove all cards of value 1, and put them in the open space at the left end of the rows: "11" to the top row, "21" to the next, and so on.
Now you have 28 cards and four spaces, called gaps, in four rows and eight columns. You start moving cards from this layout.
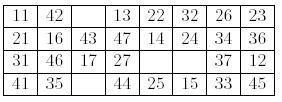
At each move, you choose one of the four gaps and fill it with the successor of the left neighbor of the gap. The successor of a card is the next card in the same suit, when it exists. For instance the successor of "42" is "43", and "27" has no successor.
In the above layout, you can move "43" to the gap at the right of "42", or "36" to the gap at the right of "35". If you move "43", a new gap is generated to the right of "16". You cannot move any card to the right of a card of value 7, nor to the right of a gap.
The goal of the game is, by choosing clever moves, to make four ascending sequences of the same suit, as follows.
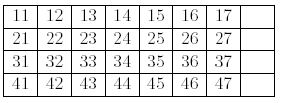
Your task is to find the minimum number of moves to reach the goal layout.
You have 28 cards labeled with two-digit numbers. The first digit (from 1 to 4) represents the suit of the card, and the second digit (from 1 to 7) represents the value of the card.
First, you shu2e the cards and lay them face up on the table in four rows of seven cards, leaving a space of one card at the extreme left of each row. The following shows an example of initial layout.

Next, you remove all cards of value 1, and put them in the open space at the left end of the rows: "11" to the top row, "21" to the next, and so on.
Now you have 28 cards and four spaces, called gaps, in four rows and eight columns. You start moving cards from this layout.

At each move, you choose one of the four gaps and fill it with the successor of the left neighbor of the gap. The successor of a card is the next card in the same suit, when it exists. For instance the successor of "42" is "43", and "27" has no successor.
In the above layout, you can move "43" to the gap at the right of "42", or "36" to the gap at the right of "35". If you move "43", a new gap is generated to the right of "16". You cannot move any card to the right of a card of value 7, nor to the right of a gap.
The goal of the game is, by choosing clever moves, to make four ascending sequences of the same suit, as follows.

Your task is to find the minimum number of moves to reach the goal layout.
Input
The input starts with a line containing the number of initial layouts that follow.
Each layout consists of five lines - a blank line and four lines which represent initial layouts of four rows. Each row has seven two-digit numbers which correspond to the cards.
Each layout consists of five lines - a blank line and four lines which represent initial layouts of four rows. Each row has seven two-digit numbers which correspond to the cards.
Output
For each initial layout, produce a line with the minimum number of moves to reach the goal layout. Note that this number should not include the initial four moves of the cards of value 1. If there is no move sequence from the initial layout to the goal layout, produce "-1".
Sample Input
4
12 13 14 15 16 17 21
22 23 24 25 26 27 31
32 33 34 35 36 37 41
42 43 44 45 46 47 11
26 31 13 44 21 24 42
17 45 23 25 41 36 11
46 34 14 12 37 32 47
16 43 27 35 22 33 15
17 12 16 13 15 14 11
27 22 26 23 25 24 21
37 32 36 33 35 34 31
47 42 46 43 45 44 41
27 14 22 35 32 46 33
13 17 36 24 44 21 15
43 16 45 47 23 11 26
25 37 41 34 42 12 31
Sample Output
0
33
60
-1
***************************************************************************************************************************

1 #include<iostream> 2 #include<string> 3 #include<cstring> 4 #include<cmath> 5 #include<queue> 6 #include<cstdio> 7 using namespace std; 8 #define LL __int64 9 #define maxn 1000000+7 10 LL hash[maxn]; 11 LL bin[34]; 12 LL endval,n,m,flag; 13 int ans,cas; 14 int tmp[4][8]; 15 int i,j,k; 16 int faval[4][8]= 17 { 18 11,12,13,14,15,16,17,0, 19 21,22,23,24,25,26,27,0, 20 31,32,33,34,35,36,37,0, 21 41,42,43,44,45,46,47,0 22 }; 23 struct node 24 { 25 LL val; 26 int mp[4][8]; 27 int cnt; 28 int blankx[4],blanky[4]; 29 }cur,now; 30 queue<node>Q; 31 32 void premap()//第一步操作都相同 33 { 34 int it,jt; 35 for(it=0;it<4;it++) 36 for(jt=1;jt<8;jt++) 37 { 38 if(cur.mp[it][jt]==11) 39 { 40 swap(cur.mp[it][jt],cur.mp[0][0]); 41 cur.blankx[0]=it; 42 cur.blanky[0]=jt; 43 } 44 else if(cur.mp[it][jt]==21) 45 { 46 swap(cur.mp[it][jt],cur.mp[1][0]); 47 cur.blankx[1]=it; 48 cur.blanky[1]=jt; 49 } 50 else if(cur.mp[it][jt]==31) 51 { 52 swap(cur.mp[it][jt],cur.mp[2][0]); 53 cur.blankx[2]=it; 54 cur.blanky[2]=jt; 55 } 56 else if(cur.mp[it][jt]==41) 57 { 58 swap(cur.mp[it][jt],cur.mp[3][0]); 59 cur.blankx[3]=it; 60 cur.blanky[3]=jt; 61 } 62 63 } 64 } 65 66 bool Is_can()//判断状态是否符合结果 67 { 68 int it,jt; 69 LL s=0; 70 for(it=0;it<4;it++) 71 for(jt=0;jt<8;jt++) 72 { 73 s+=cur.mp[it][jt]*bin[it*8+jt]; 74 } 75 if(s==endval)return true; 76 return false; 77 } 78 79 bool hash_add()//hash判重 80 { 81 int it,jt; 82 if(Is_can())flag=1; 83 int ss=(int)(cur.val%maxn); 84 while(hash[ss]!=-1&&hash[ss]!=cur.val) 85 { 86 ss+=10; 87 if(ss>=maxn) 88 ss=ss%maxn; 89 } 90 if(hash[ss]==-1) 91 { 92 hash[ss]=cur.val; 93 return true; 94 } 95 return false; 96 } 97 98 bool bfs()//bfs()判断最符合的状态 99 { 100 int it,jt,kt; 101 LL tval; 102 while(!Q.empty()) 103 Q.pop(); 104 Q.push(cur); 105 while(!Q.empty()) 106 { 107 now=Q.front(); 108 Q.pop(); 109 for(kt=0;kt<4;kt++) 110 { 111 int xx=now.blankx[kt]; 112 int yy=now.blanky[kt]; 113 memcpy(tmp,now.mp,sizeof(now.mp)); 114 for(it=0;it<4;it++) 115 for(jt=0;jt<8;jt++) 116 { 117 if(tmp[it][jt]==0)continue; 118 if(tmp[xx][yy-1]+1==tmp[it][jt]) 119 { 120 tval=now.val; 121 tval-=tmp[it][jt]*bin[it*8+jt]; 122 tval+=tmp[it][jt]*bin[xx*8+yy]; 123 swap(tmp[xx][yy],tmp[it][jt]); 124 cur.val=tval; 125 memcpy(cur.mp,tmp,sizeof(tmp)); 126 if(hash_add()) 127 { 128 if(flag) 129 { 130 ans=now.cnt+1; 131 return true; 132 } 133 memcpy(cur.blankx,now.blankx,sizeof(cur.blankx)); 134 memcpy(cur.blanky,now.blanky,sizeof(cur.blanky)); 135 cur.cnt=now.cnt+1; 136 cur.blankx[kt]=it; 137 cur.blanky[kt]=jt; 138 Q.push(cur); 139 } 140 } 141 } 142 143 } 144 } 145 return false; 146 } 147 148 int main() 149 { 150 bin[0]=1; 151 for(i=1;i<=33;i++) 152 bin[i]=bin[i-1]<<1; 153 endval=0; 154 for(i=0;i<4;i++) 155 for(j=0;j<8;j++) 156 endval+=faval[i][j]*bin[i*8+j]; 157 //cout<<"endval:: "<<endval<<endl; 158 scanf("%d",&cas); 159 while(cas--) 160 { 161 flag=0; 162 LL s=0; 163 memset(hash,-1,sizeof(hash)); 164 for(i=0;i<4;i++) 165 { 166 cur.blankx[i]=i; 167 cur.blanky[i]=0; 168 cur.mp[i][0]=0; 169 for(j=1;j<8;j++) 170 { 171 scanf("%d",&cur.mp[i][j]); 172 s+=cur.mp[i][j]*bin[i*8+j]; 173 } 174 } 175 cur.val=s; 176 cur.cnt=0; 177 premap(); 178 hash_add(); 179 if(flag) 180 printf("0 "); 181 else 182 { 183 if(bfs()) 184 printf("%d ",ans); 185 else 186 printf("-1 "); 187 } 188 } 189 return 0; 190 191 }
