矩阵与行列式的几何意义

作者：童哲
链接：https://www.zhihu.com/question/36966326/answer/70687817
来源：知乎
著作权归作者所有，转载请联系作者获得授权。

行列式这个“怪物”定义初看很奇怪，一堆逆序数什么的让人不免觉得恐惧，但其实它是有实际得不能更实际的物理意义的，理解只需要三步。这酸爽~


1，行列式是针对一个的矩阵而言的。表示一个维空间到维空间的线性变换。那么什么是线性变换呢？无非是一个压缩或拉伸啊。假想原来空间中有一个维的立方体（随便什么形状），其中立方体内的每一个点都经过这个线性变换，变成维空间中的一个新立方体。

2，原来立方体有一个体积，新的立方体也有一个体积。

3，行列式是一个数对不对？这个数其实就是 ，结束了。

就这么简单？没错，就这么简单。



所以说：行列式的本质就是一句话：

行列式就是线性变换的放大率！




理解了行列式的物理意义，很多性质你根本就瞬间理解到忘不了！！！比如这个重要的行列式乘法性质：



道理很简单，因为放大率是相乘的啊~！



你先进行一个变换，再进行一个变换，放大两次的放大率，就是式子左边。
你把“先进行变换，再进行变换”定义作一个新的变换，叫做“”，新变换的放大律就是式子右边。

然后你要问等式两边是否一定相等，我可以明确告诉你：too simple 必须相等。因为其实只是简单的把事实陈述出来了。这就好像：

“ 你经过股票投资，把1块钱放大3被变成了3块钱，然后经过实业投资，把3块钱中的每一块钱放大5倍成了5块钱。请问你总共的投资放大率是多少？”



翻译成线性代数的表达就是：





（如果有幸过50赞，我就明天再追加点行列式更好玩的东东，太晚了睡觉去了。晚安）
——————————————————————————————————————————




好的已经过50了，我来解锁新的体验哈~

上回咱们说到行列式其实就是线性变换的放大率，所以你理解了：


那么很自然，你很轻松就理解了：


so easy，因为




同时你也必须很快能理解了

“矩阵可逆” 完全等价于 “”

因为再自然不过了啊，试想是什么意思呢？不就是线性变换把之前说的维立方体给拍扁了啊？！这就是《三体》中的”降维打击”有木有！！！如来神掌有木有！！！直接把3维立方体 piaji一声~一掌拍成2维的纸片，纸片体积多少呢？当然是 0 啦！

请注意我们这里说的体积都是针对维空间而言的， 就表示新的立方体在 维空间体积为0，但是可能在维还是有体积的，只是在 维空间的标准下为0而已。好比一张纸片，“2维体积”也就是面积可以不为0，但是“3维体积”是妥妥的0。

所以凡是的矩阵都是耍流氓，因为这样的变换以后就再也回不去了，降维打击是致命性的。这样的矩阵必然是没有逆矩阵 的。这就是物理意义和图象思维对理解数学概念的重要性。



当然要证明也是小菜一碟轻而易举的：

由

可知

这怎么可能啊~？ 了，那么等于多少呢？毫无办法，只能不存在。一个矩阵怎么可能行列式不存在呢？只能是因为 不存在。所以自然不可逆。




（如果有幸过1000赞，我就再追加点行列式更亮瞎双眼的性质。）
——————————————————————————————————————————


YES！竟然真的过1000了，我来说点儿烧脑的，第一次看以下结论如果没有毁三观亮瞎双眼的刺激感，请接受阿哲的膝盖：

傅里叶变换也可以求行列式！！！


是的你没有听错，大名鼎鼎的傅里叶变换 居然也可以求行列式！！！


首先一定有很多人要问责我，是不是没有学过行列式，因为按照绝大多数教科书来说，行列式是这样定义的：




然后还有什么好说的，拿到一个矩阵各种化简然后算就好了呗，可是怎么说傅里叶变换也可以求行列式？傅里叶变换又不是一个矩阵，更别说矩阵元了。我在痴人说梦吗？

但是，等等！桥度麻袋，“傅里叶变换”里面有个"变换"，难道它也是“线性变换”？！！！


一检查，尼玛还真的是。所有函数就组成了一个向量空间，或者说线性空间。可是为什么呢？从高中咱们就熟悉的明明是函数啊，怎么就变成了向量呢？向量不是一个维空间中的箭头吗？长得也不像啊。



其实 “所有组成的集合” 确实满足一切线性空间的定义，比如：

1，向量和向量可以相加，并且有交换律

2，存在零向量 ，即处处值为零的函数

3，任何一个向量都存在一个与之对应的逆向量，使得相加之和等于零向量

以及存在数乘以及分配率等性质…… 总之“所有向量组成的集合”完美满足线性空间的8条黄金法则。



艾玛真是亮瞎了俺的钛合金左眼，原来咱们熟悉的函数身世可不一般啊，其实它是一个掩藏得很好的向量！！！对，我没有说错，因为所有函数组成的集合构成了一个线性空间！而且还是无穷维的线性空间！！！阿哲校长感动得哭了 T____T


好，下面准备亮瞎钛合金右眼吧~

一旦接受了向量是向量的设定，周围的一切都变得有趣起来了！轶可赛艇！！！


接下来不妨思考一下，傅里叶变换 是把一个函数变成了另一个函数，难道不可以理解为把一个线性空间中的向量变成了另一个线性空间中的向量吗？ 我整个人都咆哮了！！！



而且这个变换是妥妥的线性的，完美地满足线性变换的定义：

以及


因为积分变换的线性性：

的傅里叶变换的傅里叶变换+的傅里叶变换

加法达成。当然数乘也轻松满足：




于是乎，我们通过以上内容知道了一个重要的结论：

傅里叶变换其实也是线性变换，所以也可以求行列式！！！


（其实傅里叶变换作为一个线性变换不但可以求行列式，更可以求它的特征向量！！比如，以及其他很多很多牛逼的东东，恭喜你又一扇新世界的大门被打开了。千万不要小看傅里叶变换，比如量子力学不确定性原理的秘密就都在这里了）



言归正传那么傅里叶变换神秘的行列式的值 究竟是多少呢？难道这个无穷维线性变换也可以求出行列式吗？



（真相只有一个！只要收集到2000个赞阿哲就把 求出来给你看~ 求分享O(∩_∩)O~）
————————————————————————————————————————

OK，判定条件触发开始求。

很明显的问题是这是一个比较困难的问题，如果不太困难的话评论中应该有人po出了答案。因为求傅里叶变换的行列式让我们觉得没有工具可以用，行列式的定义式毫无用武之地。毕竟没有谁能够写出傅里叶变换的矩阵表达式并套用公式。

所以一定要用到其他的化简办法，例如对称性啊等等。不妨先回顾一下之前的结论，对于任何可逆线性变换有如下性质：



如果把傅里叶变换看做是一个无穷维的，那么也一定满足这个性质。所以只要求出了傅里叶变换的逆变换的行列式，求一个倒数就得到了傅里叶变换的行列式。

艾玛~ 问题变得更难了。傅里叶变换的逆变换？还好我学过。。。

若傅里叶变换是：

则它的逆变换是： （说明傅里叶变换可逆，因为表达式都出来了）

现在的问题是，正负变换，我都不会求行列式，唯一知道的是 为之奈何？我们还需要至少一个表达式能够反映二者的关系，连立起来才能够求解。

没问题，因为这两个变换真是太像了，像到几乎完全对称。差异点仅仅在于逆变换多一个乘积系数，以及积分因子多了一个负号。除此之外完全是同一个线性变换。而积分因子多一个负号是什么意思？意味着复数空间的手性定义相反，变成了，左手变成右手，或者说虚数部分取负号实数部分不变。这样的手性改变，并不会改变线性变换的体积放大率（之前的知识）。于是乎在线性变化的方法率的意义下，傅里叶变换和它的逆变换放大率是一样的（还差一个乘积系数）。

于是也就是说

结合之前的式子

我们很容以得到

（更严格来说更对称的傅里叶变换版本的行列式为1）


我去，真的可以求啊。是的，你已经求出来了，虽然神一般的无穷维行列式的计算公式并没有出现，但你确实求出来了。而且阿哲再附送大家一个彩蛋：


都说求导可以把一个函数变成另一个函数，如果我们把“求导这个操作”当做是一个线性变换，发现其实也是完全合理的：



线性性完美地满足:



那么请问"求导作为函数空间下的线性变换行列式”等于多少呢？


思考一下。。。


再思考一下。。。前方剧透请小心手滑！！！











。。。





因为，它是不可逆的！

你要问我兹次不兹次？我可以明确告诉你，不可逆的线性变换都是耍流氓，行列式都等于零。不要没事就搞个大新闻。

（全剧终，其他文章连载继续。时间太少更新不够勤，请多包涵。另外数学中的严格性在本文中并不能体现，也请海涵。）


★★★★★ 知识创造乐趣，你是你的大学 http://www.wanmen.org ★★★★★

 

===================================

矩阵的秩与行列式的几何意义

这里首先讨论一个长期以来困惑工科甚至物理系学生的一个数学问题，即，究竟什么是面积，以及面积的高维推广？

1 关于面积：一种映射

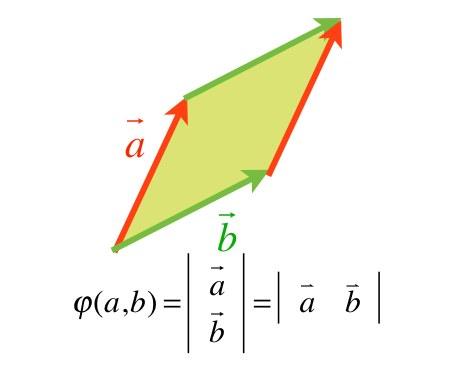
大家会说，面积，不就是长乘以宽么，其实不然。我们首先明确，这里所讨论的面积，是欧几里得空间几何面积的基本单位：平行四边形的面积。平行四边形面积的定义，几何上说是相邻两边边长乘以他们之间的夹角的正弦。

然而为了应对更一般情形和更高维度的数理问题，我们有必要把面积的定义推广开来。注意到以下事实：

面积是一个标量，它来自于（构成其相邻边）两个矢量。因此，我们可以将面积看成一个映射：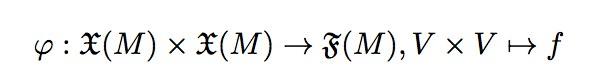

其中V就是一个矢量，V*V代表两个矢量的有序对；f就是面积的值。

下面我们将说明这个映射是一个线性映射。

从最简单的例子出发。如果第一个矢量是（1，0），第二个矢量是（0，1）；也就是说，两个矢量分别是X和Y轴上的单位正向量，那么由这两个矢量张成的四边形就是一个正方形，其面积根据定义，就是长乘以宽=1*1=1。

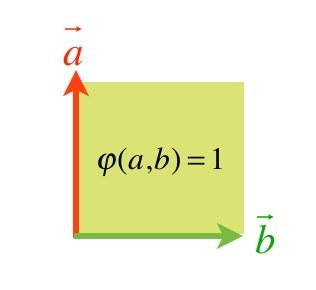
因此有：

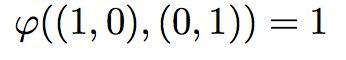
如果我们把第一个矢量”缩放“a倍，面积将会相应是原来的a倍；把第二个矢量“缩放”b倍，面积也会成为原来的b倍。如果同时缩放，很显然，面积将会变成原面积的ab倍。这表明，面积映射对于其两个操作数（矢量）的标量积是各自线性的，如下：

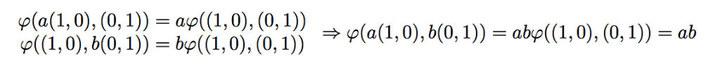
最后，我们要说明，面积映射对于其操作数（矢量）的矢量加法也是线性的。因为矢量加法操作的本身是线性的，那么其面积映射理应对此也是一个线性映射。这里我们打算从几个实际的例子出发，说明映射的加法线性性的后果。

显然（两个共线矢量所张成的平行四边形还是一条线，因此面积为0）：

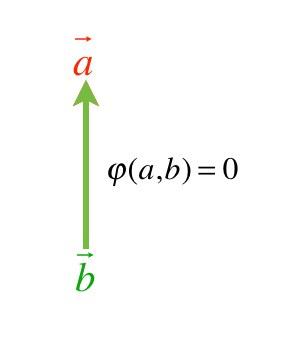
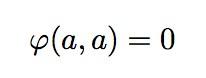
假定面积映射是一个关于矢量加法的线性映射，那么我们有：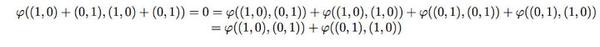

注意计算过程中用到了上面的结论。这说明：

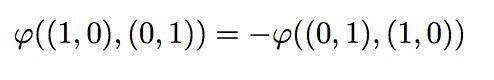
也就是说，交换相互垂直操作数矢量的顺序，面积映射取负。孰正孰负取决于认为的定义。一般，我们把X轴单位矢量在前，Y轴单位矢量在后，从X轴到Y轴张成的一个平行四边形的面积，取做正号。

1.1 右手定则

由此我们引入右手定则。注意右手定则只在三维空间中有效。如果以X正方向为首，Y正方向为尾，右手定则告诉我们，纸面向外是面积的正方向；如果反过来，那么纸面向内就是该面积的正方向，与规定的正方向相反，取负号。那么面积正负号的几何意义就明显了。

由此，我们不难得到平面内任意两个矢量所张成的平行四边形的面积（*）：

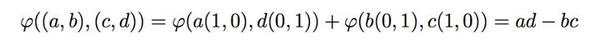
我们不难看到，所谓面积就是一个2X2矩阵的行列式：

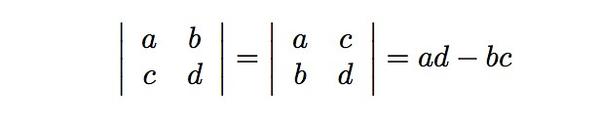如下图。

其中第一行就是我们的第一个行向量(a,b)；第二行就是第二个行向量(c,d)。或者第一列是第一个列向量(a,b)^T, 第二列是第二个列向量(c,d)^T。这取决于我们把矢量写成行向量（前者）还是列向量（后者）的形式。

1.2 行列式的计算性质

由此我们很容易能发现，行列式的值与把矢量写成列向量横排还是行向量竖排的方式是无关的。这也就是为什么说，在计算行列式时，行和列的地位是对等的。并且注意到，由上述分析，交换矢量的顺序，面积的值取负号，这也就是为什么行列式中，交换列向量或者行向量一次，就要取一次负号的原因。另外，行列式的其他计算性质，都一一反映在面积映射的线性性之中。

由此我们可见，行列式就是关于“面积”的推广。他就是在给定一组基下，N个向量张成的一个N维广义四边形的体积。这就是行列式的本质含义。

2，行列式的推广

由上，我们可以轻松推广到三维体积的计算：

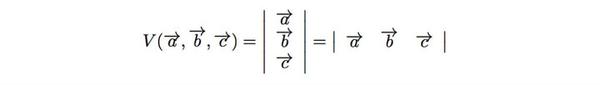
注意到，行列式的定义，是每一行各取一个不同列的元素的乘积并且符号和所谓的逆序性有关（PARITY）。所谓逆序性，其几何意义就是在规定了一个正方向之后（比如从1,2,3,4,5...N这个顺序定义为正号），交换任意一对数都取一次负号。这样的性质我们在上述的面积函数中已经有所看到，实际上体积，更高维度的广义体积，也有正方向之说，只不过已经难以用右手法则（以及叉乘）来形象说明罢了。右手定则的局限性也是将高维面积推广成行列式表达的一个动机之一。

对于这种交换任何一对指标（操作数）就改变符号的性质，我们叫做：反对称（ANTISYMMETRIC）性。之所以要取不同行不同列元素的乘积，是因为如果有任意两个元素是同行（列）的，那么交换他们的列指标，乘积不变但符号要相反，这乘积必须是0，也就是在行列式的值中不予体现。

行列式的定义之所以这么冗杂，就是来自于面积映射的反对称性。实际上面积映射是一个2-FORM，把2-FORM拓展到任意的R-FORM，我们能看到R-FORM的形式和一个R乘R矩阵的行列式是完全一致的。

由上我们已经可以看到，2-FORM代表的是平面内的面积；3-FORM自然而然就是3维空间内的体积；4-FORM是4维空间里的超体积。以此类推。而实际上，由上我们已经看到，将这些矢量在给定的基坐标下写成矩阵（必定是方阵），矩阵的行列式就是对应的面积（体积）。这个推广的证明各位应该能在任何一本线性代数的专门教材中看到（如果没有的话可以自证）。

3，线性无关的几何意义

记空间的维度为N，给定一组矢量，什么是他们线性无关性？我们下面将说明，一组矢量的线性相关性本质上，是描述他们所张成的广义平行四边形体积是否为NULL（零）。

我们仍然从最简单的2维空间出发。如果两个2维空间的向量是线性相关的，那么就是说，其中一个与另外一个共线，也就是说，他们所张成的四边形，面积是零。反之，如果线性无关，则不共线，则面积不为零。

同理，如果三个三维空间的向量是线性无关的，那么他们三者就不共面。因此他们所张成的平行六面体，体积不是零。

更进一步地，我们知道，二维空间如果给定三个向量，他们必定共面（二维空间内不可能存在一个“体积”），因此他们必定线性相关。推而广之，我们不难理解，为什么一个维度为N的空间内，任意一组M个向量（M>N）必定线性相关了：因为维度大于空间维度的超平形四边体不存在。

由此我们得到一个一一对应的关系：

N个向量线性无关 == 他们所张成的N维体体积不为零

反之，如果N个向量线性相关，那么他们所张成N维体，体积为零。

例如，一对共线矢量张成的平行四边形，退化成一个线，其面积显然是0；一组共面的三个矢量张成的平行六面体，退化成一个面，其体积显然是0。

因为我们已经知道行列式与面积的关系，因此我们有结论：

线性无关矢量组成的矩阵的行列式不为零；线性相关矢量组成的矩阵的行列式必为零。

4，行列式与矩阵的逆

我们知道，行列式为0的矩阵，不可逆；行列式不为零的矩阵，可逆。我们不禁要问，代表面积的行列式，是如何和线性变换的可逆性联系在一起的呢？

当我们理解了线性变换的几何意义之后，就不难解答了。我们现陈述如下：

记线性变换的矩阵为A。

如果我们把空间中一组线性无关的矢量都写成列向量的形式，那么他们所张成的N维体体积不为零，根据上面的分析，其值由行列式给出。向量经过线性变换A变换之后，得到的新向量形式如下：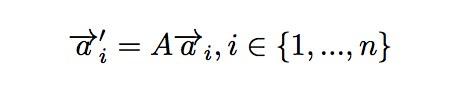

注意到A是一个N*N的矩阵，向量是列向量。

变换前，N维体的体积是：

变换之后，N维体的体积是（注意到，第二个等式实际上说明了几何意义是如何定义矩阵乘法的，也就是N*N矩阵A和另外一个N个列向量组成的N*N矩阵的乘法）：

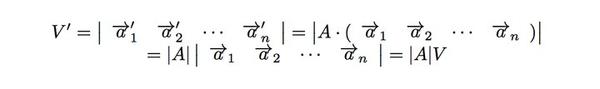
A的行列式如果不为零，则代表这个变换后，N维体的体积不是NULL。又结合线性无关与体积的性质，我们可以说：

如果A的行列式不为零，那么A可以把一组线性无关的矢量，映射成一组新的，线性无关的矢量；A是可逆的（一对一的映射，保真映射，KERNEL是{0}）

如果A的行列式为零，那么A就会把一组线性无关的矢量，映射成一组线性相关的矢量；A就不是可逆的（非保真映射，KERNEL不是{0}。我们可以研究他的陪集）

如果A的行列式为负数，那么A将会改变原N维体体积的朝向。

从线性无关到线性相关，其中丢失了部分信息（例如坍缩成共线或者共面），因此这个变换显然就是不可逆的。线性是否无关和所张成N维体的体积有直接关系，这个体积值又与A的行列式有关。因此我们就建立了A的行列式与其是否可逆的几何关系。

举例说明，我们假设A是一个3维的矩阵。如果映射前，有一组三个线性无关的矢量，我们知道它们张成的体积不是0；经过映射后，他们对应的新矢量也能张成一个平行六面体，那么这个平行六面体的体积就是原体积乘以A的行列式。

显然，如果A的行列式是0，那么变换后的新“平行六面体"的体积将不可避免的也是0。根据上文的结论，我们有：变换后的这一组新矢量线性相关。

结论：

线性变换A的行列式是否为零，就代表了其映射的保真性，也即，能不能把一组线性无关的矢量变换成另一组保持无关性的矢量。

5，秩

有时候，虽然A并不能保持把空间一组最大数目矢量的线性无关性，但它能保证一组更少数目矢量的线性无关性。这个数目往往少于A的维度（或者说，线性空间的维度），这个数目就叫做线性变换A的秩。

例如，一个秩为2的三乘三矩阵A。因为秩小于3，那么任何一个3维六面体经过他的变换后，体积都为零（退化一个面）；但存在一个面积不为零的面，在变换之后还可以是一个非零面积的面。

所谓一个线性变换的秩，无非就是变换后，还能保持非零体积的几何形状的最大维度。

理解了秩，行列式和可逆性的几何意义，我们就能随意构造一些线性变换A，使得他要么保全所有的几何体，要么将特定维度特定结构的几何体，压缩成更低维度的几何体。这不就是所谓的“降维打击”么。。所以说，三体中的终极必杀，其实也就是一个行列式为0，秩比维度少1的一个线性变换而已。

更高维度下的推广，还希望读者自己去进行；此外上文中关于面积函数线性性的证明，也交给读者自行去严格验明。

2012.11.10

(c) Bo Zeng

* 不难证明其正确性