1、标准正交矩阵
假设矩阵Q有列向量q1,q2,...,qn表示,且其列向量满足下式:
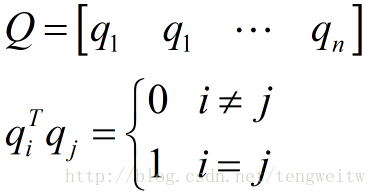
则
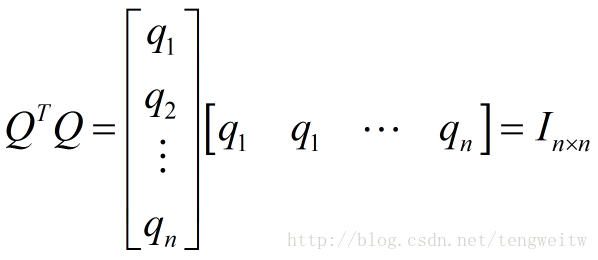
若Q为方阵,由上面的式子则有
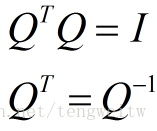
我们举例说明上述概念:
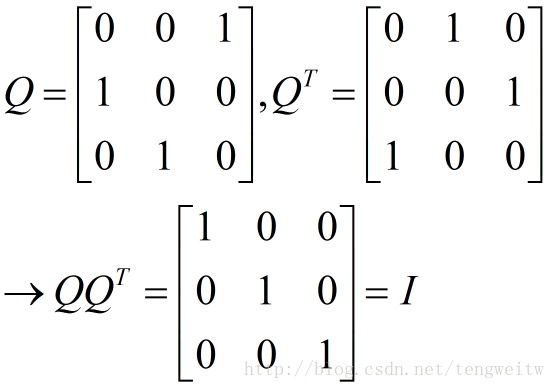
2、标准正交矩阵的好处
上面我们介绍了标准正交矩阵,那么标准正交矩阵的用处在哪? 下面以两方面来说明标准正交矩阵的用处:
求解Ax=b
在前面文章 《正交投影、格拉姆施密特正交(一)》中,有下式:
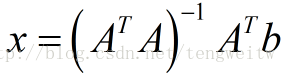
当矩阵A为标准正交矩阵Q时,由于正交矩阵与其转置的乘积为单位矩阵,则上式可以转化为:
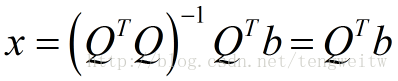
可以发现,求x时不需要矩阵Q的逆,只需要知道转置即可,这样简化了计算。
求解投影矩阵
在前面文章 《正交投影、格拉姆施密特正交(一)》中,
投影矩阵的通式可以表示为:
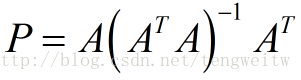
当矩阵A为标准正交矩阵Q时,由于正交矩阵与其转置的乘积为单位矩阵,则上式可以转化为:
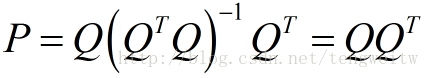
这样就将投影矩阵简单化了。
3、Gram-Schmidt正交化
任何复杂问题的求解都可以从简单的问题出发。聪明的数学家不会羞于考虑小问题,因为当最简单的情况弄得明明白白时,一般的形式就容易理解了。并且,简单的情况不仅帮我们发现一般的公式,而且还提供了一种便利的核查方法,看看我们是否犯下了愚蠢的错误。下面我们就从简单的二维情况讨论:
### 二维情况
假设原来的矩阵为[a,b],a,b为线性无关的二维向量,下面我们通过Gram-Schmidt正交化使得矩阵A为标准正交矩阵:
假设正交化后的矩阵为Q=[A,B],我们可以令A=a,那么我们的目的根据AB=I来求B。如下面的二维情况所示,B的方向与A成90度。图中还表明,B可以表示为b向量与b向量在a上的投影的误差向量。由《正交投影》中的结论可知,有如下关系成立:
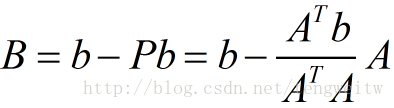
### 三维情况
假设原来的矩阵为[a,b,c],a,b,c为线性无关的二维向量,正交化后的矩阵为Q=[A,B,C],我们可以令A=a,则可以根据二维情况得到如下猜想:
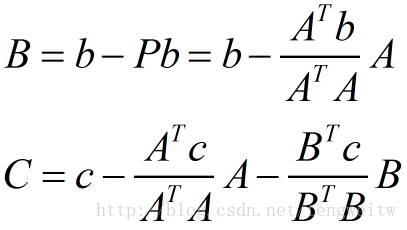
上式显然满足AB=0,AC=0,BC=0。
下面我们用实例说明正交化的过程:
假设矩阵为[a,b]
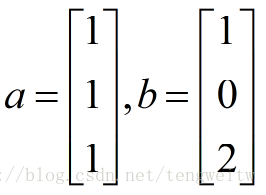
则由二维情况的结论可知:
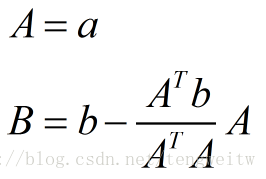
把具体数值代入得:
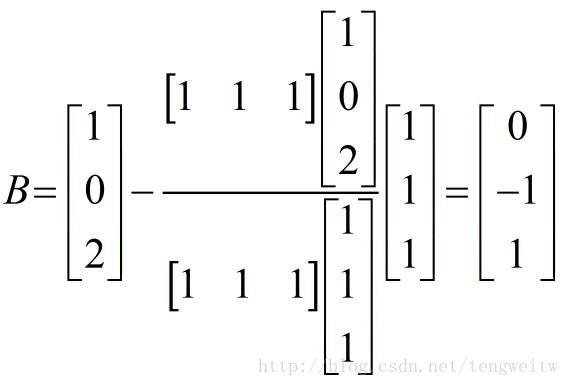
经过归一化得:
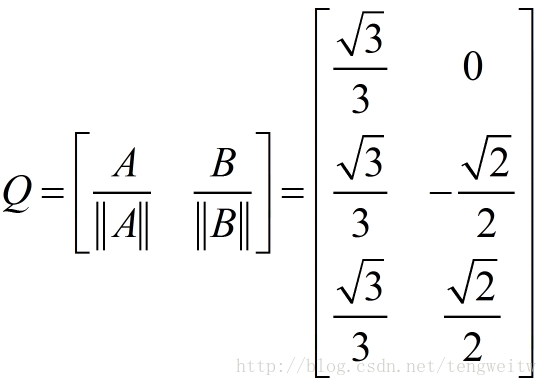
Q即是我们经过正交化后的正交矩阵。