Q-Q(Quantile-Quantile)图是用来判断两个数据集是否来自相同的分布,比如正态分布、均匀分布。如下图:
Q-Q 图
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
iris = load_iris()
X = iris.data
y = iris.target
plt.figure(figsize=(16, 8))
plt.subplot(1, 2, 1)
# 变量分布
sns.distplot(X[:, 1], fit=stats.norm)
plt.subplot(1, 2, 2)
# 变量 Q-Q 图
stats.probplot(X[:, 1], plot=plt) # 默认 dist='norm',可以为其它分布
plt.show()
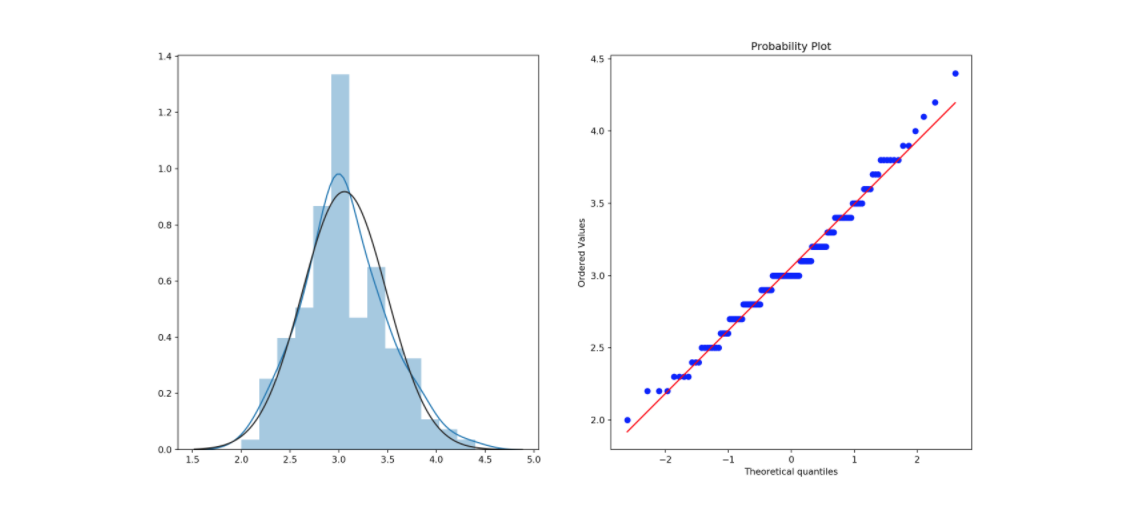
上面左图是变量的分布情况,右图是变量的 Q-Q 图,点基本都落在同一条直线上,说明此变量满足正态分布。其中,x 轴为标准正态分布的分位坐标,y 轴为变量对应的分位坐标。
其实,如果两个数据集来自相同的分布,它们的 Q-Q 图分位点位于一条直线上,例如,我们有两个正态分布数据集,x 为标准正态分布,y 为标准差为 3,均值为 2 的正态分布。如下:
import numpy as np
import matplotlib.pyplot as plt
# 来自标准正态分布的数据集
x = np.random.randn(1000)
# 来自标准差为 3,均值为 2 的正态分布
y = 3*np.random.randn(10000) + 2
# 分别找到它们的 20 个分位点
x_p = np.percentile(x, np.arange(0, 101, 5))
y_p = np.percentile(y, np.arange(0, 101, 5))
plt.figure()
plt.plot(x_p, y_p, "bo")
plt.xlabel("x quantiles")
plt.ylabel("y quantiles")
plt.title("Q-Q Plot")
plt.show()
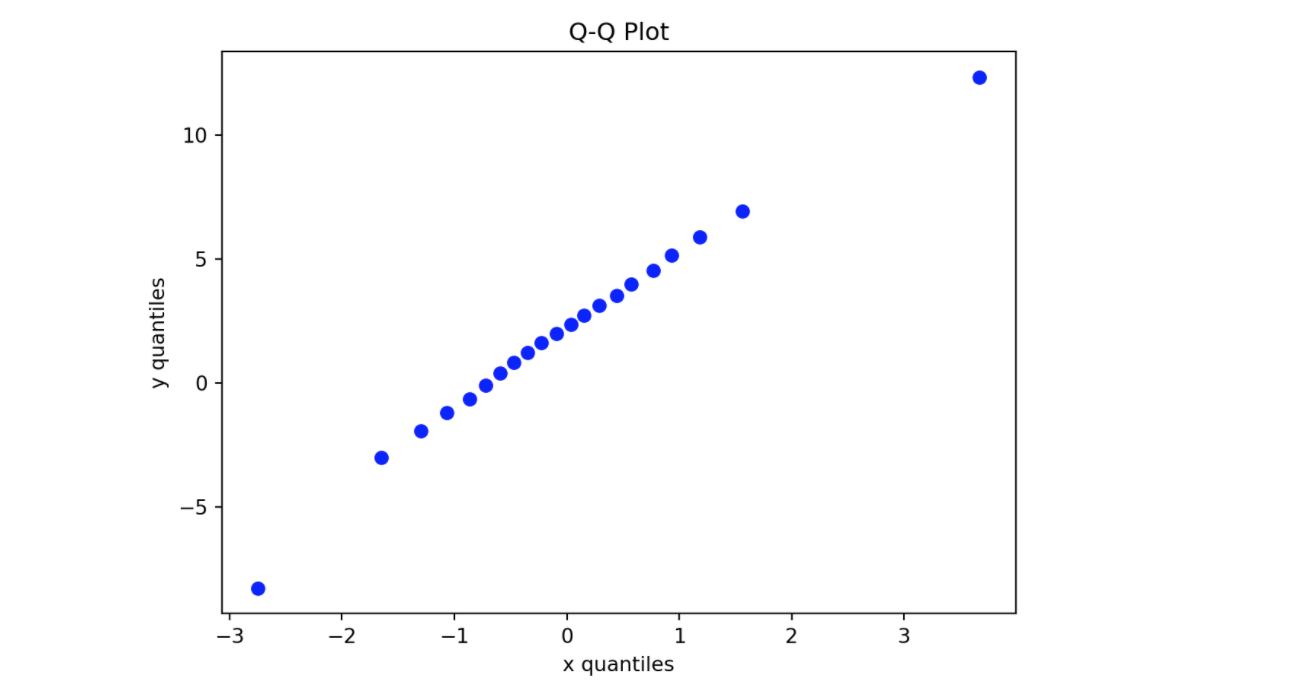
在上面代码可以看到,x 和 y 都属于正态分布,而从点的产生方式看到,y 点和 x 点呈线性关系。
正态性假设在很多统计检验中非常重要,Q-Q 图是评价正态性的一种方式。但是正态性并不是你评价数据的唯一方式,你也可以用一个连续分布作为对比数据(例如均匀分布),只要能计算出数据的分位数。事实上,通常会将我们的数据同不同的分布作 Q-Q 图,看其具体符合哪种分布。