以前也看过hashMap源码不过是看的jdk1.7的,由于时间问题看的也不是太深入,只是大概的了解了一下他的基本原理;这几天通过假期的时间就对jdk1.8的hashMap深入了解了下,相信大家都是对红黑树和hashMap的扩容机制resize()比较感兴趣,红黑树也是jdk1.8对hashMap新加的一种数据结构,单纯的树形结构挺简单的,不过红黑树是一种自动保持平衡的树形结构,那就比较复杂了,可以通过我另一个博客可以先看一下红黑树的原理再看hashMap中的红黑树就简单多了连接<<<<<,hashMap的扩容机制resize()连接<<<<,废话不多说看代码(一些解释都在代码中)
/** * 插入树形类型的元素 * Tree version of putVal. * * 操作:将插入节点的hash值与每个节点的hash值进行比较, * 如果是小于那下一次插入节点就与当前节点的左子节点比,反之则与右子节点比, * 直到当前节点的(左或右)子节点为null,将其插入; * 每当插入一次节点都会调用一次方法balanceInsertion(root, x)将红黑树进行一个平衡操作 */ final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab, int h, K k, V v) { Class<?> kc = null; boolean searched = false; //获取树的根节点 TreeNode<K,V> root = (parent != null) ? root() : this; for (TreeNode<K,V> p = root;;) { int dir, ph; K pk; //h:插入节点的hash值 //p:遍历到的当前节点 if ((ph = p.hash) > h) dir = -1; else if (ph < h) dir = 1; else if ((pk = p.key) == k || (k != null && k.equals(pk))) return p; else if ((kc == null && (kc = comparableClassFor(k)) == null) || (dir = compareComparables(kc, k, pk)) == 0) { if (!searched) { TreeNode<K,V> q, ch; searched = true; if (((ch = p.left) != null && (q = ch.find(h, k, kc)) != null) || ((ch = p.right) != null && (q = ch.find(h, k, kc)) != null)) return q; } dir = tieBreakOrder(k, pk); } TreeNode<K,V> xp = p; if ((p = (dir <= 0) ? p.left : p.right) == null) { Node<K,V> xpn = xp.next; TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn); if (dir <= 0) xp.left = x; else xp.right = x; xp.next = x; x.parent = x.prev = xp; if (xpn != null) ((TreeNode<K,V>)xpn).prev = x; //balanceInsertion(root, x):此方法是对红黑树进行平衡操作 moveRootToFront(tab, balanceInsertion(root, x)); return null; } } } /** * 插入元素 平衡红黑树的方法 * * 注:不管遇到一下三种情况任意一种情况就会进行平衡调整 ,反之不需要;如果x节点是第1种情况,必然会经历2,3;如果x节点是第3种情况不会经历1,2; * * 1. 插入节点的父节点和其叔叔节点(祖父节点的另一个子节点)均为红色的; * * 2. 插入节点的父节点是红色,叔叔节点是黑色,且插入节点是其父节点的右子节点; * * 3. 插入节点的父节点是红色,叔叔节点是黑色,且插入节点是其父节点的左子节点。 * * @param root * @param x * @return */ static <K, V> TreeNode<K, V> balanceInsertion(TreeNode<K, V> root, TreeNode<K, V> x) { //将插入的节点涂成红色 x.red = true; //此时x节点是刚插入的节点 // 这些变量名不是作者随便定义的都是有意义的。 // xp:x parent,代表x的父节点。 // xpp:x parent parent,代表x的祖父节点 // xppl:x parent parent left,代表x的祖父的左节点。 // xppr:x parent parent right,代表x的祖父的右节点。 for (TreeNode<K, V> xp, xpp, xppl, xppr;;) { //如果x.parent==null证明x是根节点,并将x(根节点)返回;平衡完毕。 if ((xp = x.parent) == null) { //将根节点涂成黑色 x.red = false; return x; //只要进入此if就不会满足注释中3条件的任意一个,直接将root返回;平衡完毕。 } else if (!xp.red || (xpp = xp.parent) == null) return root; //若父节点是祖父节点的左子节点,与下面的完全相反,本质是一样的 if (xp == (xppl = xpp.left)) { //x节点的祖父节点的右子节点(叔叔节点)不为null且是红色,父节点必然也是红色,此时满足第1种情况。 //操作:1.将祖父节点的右子节点(叔叔节点)、父节点涂为黑色 // 2.将祖父节点涂为红色 // 3.将祖父节点赋给x(参照节点的变更) if ((xppr = xpp.right) != null && xppr.red) { xppr.red = false; xp.red = false; xpp.red = true; x = xpp; //进入else 说明已经是第2或第3种情况了 } else { //第2种情况 // 操作:1.标记节点变为x。 // 2.左旋 // 3.x的父节点、x的祖父节点随之变化 if (x == xp.right) { root = rotateLeft(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } //第3种情况 //操作 1.将父节点涂黑 // 2.祖父节点涂红 // 3.右旋 if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; root = rotateRight(root, xpp); } } } } else {//若父节点是祖父节点的右子节点,与上面的完全相反,本质一样的 if (xppl != null && xppl.red) { xppl.red = false; xp.red = false; xpp.red = true; x = xpp; } else { if (x == xp.left) { root = rotateRight(root, x = xp); xpp = (xp = x.parent) == null ? null : xp.parent; } if (xp != null) { xp.red = false; if (xpp != null) { xpp.red = true; root = rotateLeft(root, xpp); } } } } } }
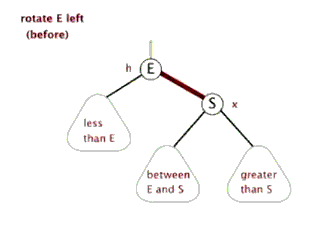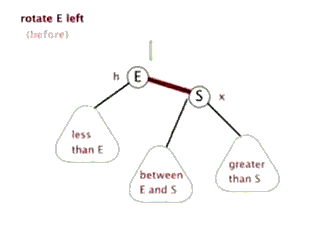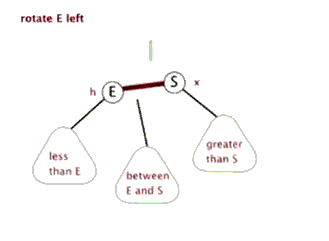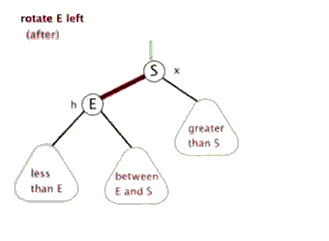
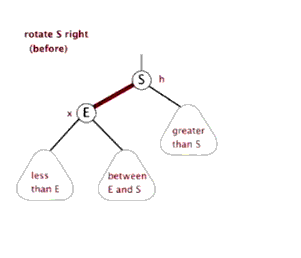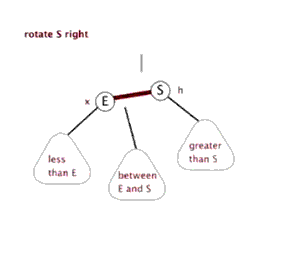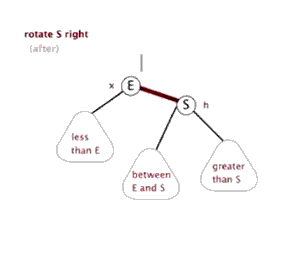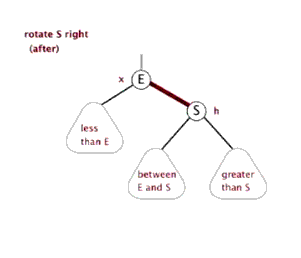
左旋和右旋只通过代码说,没有图听不明白,必须通过上边说的红黑树原理的那篇博客结合代码才容易看明白,先上一个那篇博客中的左旋和右旋的动态图先了解一下
左旋有个很萌萌哒的动态示意图,可以方便理解:
右旋也有个很萌萌哒的动态示意图,可以方便理解
hashMap的代码我就不贴了大家可以自己看一下