定义:合并排序就是通过将两个有序的序列合并为一个大的有序的序列的方式来实现排序。
合并排序是一种典型的分治算法:首先将序列分为两部分,然后对每一部分进行循环递归的排序,然后逐个将结果进行合并。
合并排序最大的优点是它的时间复杂度为O(nlgn)。他还是一种稳定性排序,也就是相等的元素在序列中的相对位置在排序前后不会发生变化。他的唯一缺点是,需要利用额外的N的空间来进行排序。
效果图:

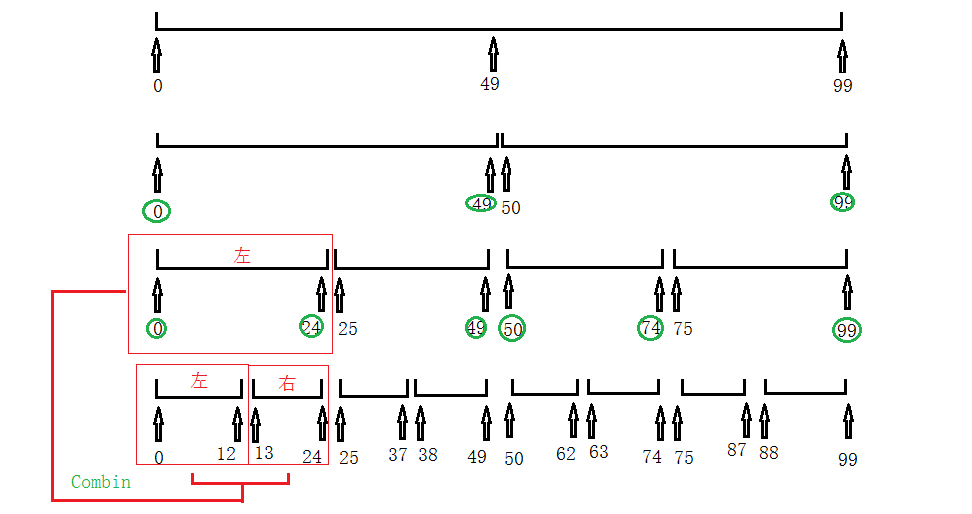
如果以排序38,27,43,3,9,82,10为例,将合并排序画出来的话,可以看到如下图:

void Combin(vector<int>& Vector,vector<int>& tmp, int left, int middle, int right) //合并两个有序区间
{
int start1 = left;
int start2 = middle + 1;
int index = left;
while (start1 != middle + 1 && start2 != right + 1)
tmp[index++] = Vector[start1] < Vector[start2] ? Vector[start1++] : Vector[start2++];
if (start1 == middle + 1)
{
while (start2 != right + 1)
tmp[index++] = Vector[start2++];
}
else
{
while (start1 != middle + 1)
tmp[index++] = Vector[start1++];
}
while (left != right + 1)
{
Vector[left] = tmp[left];
left++;
}
}
void Section(vector<int>& Vector, vector<int>& tmp, int left, int right) //分段排序
{
int middle = left + (right - left) / 2;
if (middle - left + 1 > 13) //优化 1
Section(Vector,tmp,left, middle);
else
InsertSort(Vector, left, middle);
if (right - middle > 13)
Section(Vector,tmp, middle + 1, right);
else
InsertSort(Vector, middle + 1, right);
if(Vector[middle] < Vector[middle+1]) //优化 2
Combin(Vector,tmp, left, middle, right);
}
void MergeSort(vector<int>& Vector)
{
vector<int> tmp;
tmp.resize(Vector.size());
Section(Vector, tmp, 0, Vector.size() - 1);
}
算法分析:
1. 合并排序的平均时间复杂度为O(nlgn)

我们对数组N进行MergeSort的时候,是逐级划分的,这样就形成了一个满二叉树,树的每一及子节点都为N,树的深度即为层数lgN+1
所以时间复杂度为: O(N)=(lgN+1)N=NlgN+N=NlgN
2.在合并排序中,我们要创建一个大小为N的辅助排序数组来存放初始的数组或者存放合并好的数组,所以需要长度为N的额外辅助空间。
所以空间复杂度为: S(N) = N
改进:
1. 当划分到较小的子序列时,通常可以使用插入排序替代合并排序
2.当已排好序的左侧的序列的最大值<=右侧序列的最小值的时候,表示整个序列已经排好序了。
3. 并行化
用途:
合并排序和快速排序一样都是时间复杂度为nlgn的算法,但是和快速排序相比,合并排序是一种稳定性排序,也就是说排序关键字相等的两个元素在整个序列排序的前后,相对位置不会发生变化,这一特性使得合并排序是稳定性排序中效率最高的一个。在Java中对引用对象进行排序,Perl、C++、Python的稳定性排序的内部实现中,都是使用的合并排序。