堆常用来实现优先队列,在这种队列中,待删除的元素为优先级最高(最低)的那个。在任何时候,任意优先元素都是可以插入到队列中去的,是计算机科学中一类特殊的数据结构的统称。
一、堆的定义
最大(最小)堆是一棵每一个节点的键值都不小于(大于)其孩子(如果存在)的键值的树。大顶堆是一棵完全二叉树,同时也是一棵最大树。小顶堆是一棵完全完全二叉树,同时也是一棵最小树。
注意:
- 堆中任一子树亦是堆。
- 以上讨论的堆实际上是二叉堆(Binary Heap),类似地可定义k叉堆。
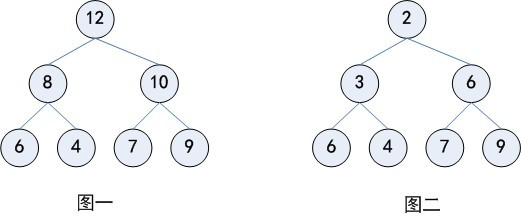
下图分别给出几个最大堆和最小堆的例子:
二、支持的基本操作
堆支持以下的基本操作:
- build: 建立一个空堆;
- insert: 向堆中插入一个新元素;
- update:将新元素提升使其符合堆的性质;
- get:获取当前堆顶元素的值;
- delete:删除堆顶元素;
- heapify:使删除堆顶元素的堆再次成为堆。
某些堆实现还支持其他的一些操作,如斐波那契堆支持检查一个堆中是否存在某个元素。
三、存储结构与操作
堆里面的元素可以使用数组来存储,同时还要存储对的容量和长度。因此,可以定义如下结构体:
struct HeapStruct{ int *Element; int size; int capacity; };
在创建堆时,
将堆中元素保存在数组中时,从数组的第一个元素开始存储数据,数组的长度为 堆的长度+1,数组的第0号元素存储的是比堆中所有元素大的哨兵,以便于后面更快的操作
HeapStruct Creat_heap(int Maxsize)
{/*创建容量为Maxsize的空最大堆*/ HeapStruct *h=new (HeapStruct); h->Element=new int[Maxsize+1]; h->size=0; h->capacity=Maxsize; h->Element[0]=MaxData; /*MaxData 位大于堆中所有可能的值,以便于后面更快的操作*/
return h; }
堆的插入:
每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列,现在的任务是将这个新数据插入到这个有序数据中——这就类似于直接插入排序中将一个数据并入到有序区间中。
插入的步骤如下:
1、将数据插入到数组的末尾
2、比较其父节点与插入点的数据大小,使其满足大(小)堆的条件
3、一次向上递归直到父节点大(小)于琦子节点
void Heap_Insert(HeapStruct *h,int t) {/*将元素t插入堆h,其中h->Element[0]已设置为哨兵*/ if(IsFull()) { cout << "堆已满"<<endl; return ; } int i=++ h->size; /*插入数据的位置*/ while( i>0&&h->Element[i/2]<t) /*父节点小于子节点,由于根节点从1开始编号,故i的父节点的编号为i/2*/ {
h->Element[i]=h->Element[i/2];
i/=2; /*向下过滤节点*
}
h-Element[i]=t; /*将t插入*/
}
堆的删除:
堆的删除通常是取出根节点的数据,并删除节点,其实删除其他节点也是类似的,只是左后需要将最后一个数与删除节点的父节点和子节点都比较(应该是先与子节点比较,然后与父节点比较,因为与父节点比较时,需要保证父节点是堆)。对于删除根节点,由于根节点没有父节点,因此只需和其父节点比较。
int Heap_Delete(Heap_Struct *h) { int MaxData=h->Element[1]; int tmp=h->Element[h->size--];/*取出最后一个元素并将堆的长度减1*/ int i=1; while(2*i<=h->size && h->Element[2*i]>tmp) { if((2*i+1)<=h->size && h->Element[2*i+1]>h->Element[2*i] && h->Element[2*i+1]>tmp) /*右节点存在且大于左节点且大于插入的值,则将右节点移到其父节点并继续向上过滤*/ { h->Element[i]=h->Element[2*i+1];; i=2*i+1; } else if(h->Element[2*i]>tmp) /*左节点大且大于插入的值,则将左节点移到其父节点并继续向上过滤*/ { h->Element[i]=h->Element[2*i]; i=2*i; } else break; } h->Element[i]=tmp; /*将最后一个数插到堆中*/ return MaxData; }
最大(小)堆的建立
在应用最大堆时(譬如堆排序),需要先建立最大堆。建立最大堆有两种方法,
一种是通过堆的插入操作,将N个元素一个个相继插入到一个初始为空的堆中,其时间复杂对为O(NlogN)。
另一种方法是将N个元素按顺序存入,先满足完全二叉树的结构特性,然后,调整各节点的位置以满足最大堆的有序特性,建堆的时间复杂度为O(N)。
建堆过程:根据堆中某根节点,其左右节点也为堆。因此反过来,应该先保证子节点为堆,然后在调整父节点使其为堆。以下面的一个堆为例:
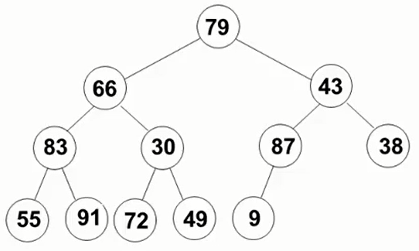
根据上面分析,首先看最后一个子节点与其父节点是否构成堆,然后依次往前遍历,确保每个节点满足堆的特性。所以首先考虑87,然后考虑30、83、43、66、79
Heap_Struct* Heap_Construct(int *arr,int len) {/*根据长度为len的数组创建最大堆*/ Heap_Struct *H_tmp= new Heap_Struct; H_tmp->Element=new int[len+1]; H_tmp->size=len; H_tmp->capacity=len; int i,start,tmp=0; int parent,child; for (i=1;i<len+1;i++) { H_tmp->Element[i]=arr[i-1]; if(tmp<arr[i]) tmp=arr[i]; } H_tmp->Element[0]=tmp+5; start=i/2; for(i=start;i>0;i--) { parent=i; while(2*parent<=H_tmp->size) //存在子节点,则按照前面删除根节点后重构堆的办法,以第i个节点为根,重构子树的堆 { if(2*parent+1<=len && H_tmp->Element[2*parent+1]>H_tmp->Element[2*parent] && H_tmp->Element[2*parent+1]>H_tmp->Element[parent]) { tmp=H_tmp->Element[parent]; H_tmp->Element[parent]=H_tmp->Element[2*parent+1]; H_tmp->Element[2*parent+1]=tmp; parent=2*parent+1; } else if(H_tmp->Element[2*parent]>H_tmp->Element[parent]) { tmp=H_tmp->Element[parent]; H_tmp->Element[parent]=H_tmp->Element[2*parent]; H_tmp->Element[2*parent]=tmp; parent=2*parent; } else break; } } return H_tmp; }
例:
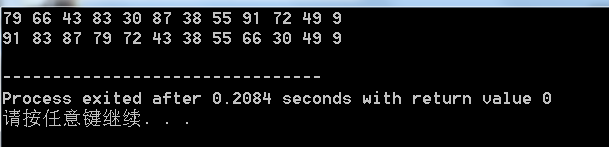
#include <iostream> using namespace std; struct Heap_Struct{ int *Element; int size; int capacity; }; Heap_Struct* Heap_Construct(int *arr,int len) {/*根据长度为len的数组创建最大堆*/ Heap_Struct *H_tmp= new Heap_Struct; H_tmp->Element=new int[len+1]; H_tmp->size=len; H_tmp->capacity=len; int i,start,tmp=0; int parent,child; for (i=1;i<len+1;i++) { H_tmp->Element[i]=arr[i-1]; if(tmp<arr[i]) tmp=arr[i]; } H_tmp->Element[0]=tmp+5; start=i/2; for(i=start;i>0;i--) { parent=i; while(2*parent<=H_tmp->size) //存在子节点 { if(2*parent+1<=len && H_tmp->Element[2*parent+1]>H_tmp->Element[2*parent] && H_tmp->Element[2*parent+1]>H_tmp->Element[parent]) { tmp=H_tmp->Element[parent]; H_tmp->Element[parent]=H_tmp->Element[2*parent+1]; H_tmp->Element[2*parent+1]=tmp; parent=2*parent+1; } else if(H_tmp->Element[2*parent]>H_tmp->Element[parent]) { tmp=H_tmp->Element[parent]; H_tmp->Element[parent]=H_tmp->Element[2*parent]; H_tmp->Element[2*parent]=tmp; parent=2*parent; } else break; } } return H_tmp; } int main() { int arr[]={79,66,43,83,30,87,38,55,91,72,49,9}; for(int i=0;i<12;i++) cout << arr[i] <<' '; cout << endl; int len=12; Heap_Struct* h=Heap_Construct(arr,len); for(int i=1;i<13;i++) cout << h->Element[i] << ' '; cout <<endl; return 0; }
输出为: