带环链表的入口

带环的单链表：

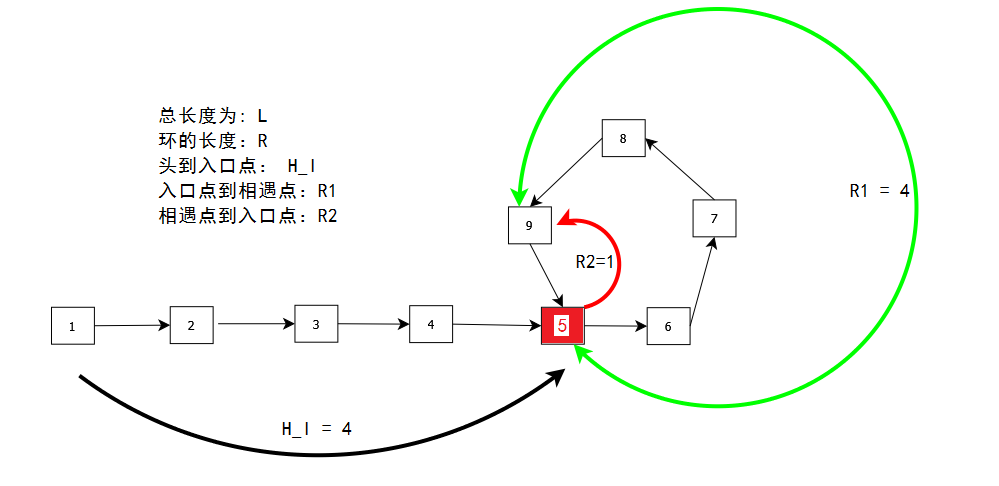
如上图，List 为一个带有环的单链表，环的大小为5；

证明：

S 为 slow 指针相遇前走的距离，2S 为 fast 指针相遇前走过的距离；

∵ 2S = S + n*R;        //n slow，fast指针相遇前 fast 多经历的圈数

　 S = H_I + R1；

 ∴S = n*R; 

∴n*R = H_I  + R1;     

∵ R1 + R2 = R;

∴(n-1)*R = H_I - R2;  

∴(n-1)*R + R2 = H_I;       //结论：(交点到入口点的距离+环长度的整数倍) = 头到入口点的距离

template<class T>
ListNode<T>* List<T>::IsRingList()
{
    if (_head == NULL)
        return NULL;
    Node* fast = _head,* slow = _head,* Input;
    while (fast && fast->_next)
    {
        if (fast == slow)     //链表带环 输出环的长度和入口点
        {
            int count = 1;
            do
            {
                slow = slow->_next;
                fast = fast->_next->_next;
                ++count;
            } while (fast == slow);
            cout << "环的节点的个数为：" << count << endl;

            while (Input == slow)
            {
                Input = Input->_next;
                slow = slow->_next;
            }
            return Input;
        }
　　　　　 slow = slow->_next;

         fast = fast->_next->_next;

} return NULL; }