https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2432
求三角形的三条三等分线的交点所形成的三角形的面积
证明等边:
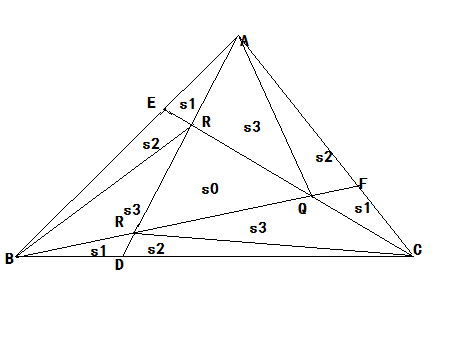
如图:证明等边三角形
s1+s2+s3+s1=(1/3)s;
BD:DC=1:2 s2=2s1
s=3*(s1+s2+s3+s1)=3s1+3s2+3s3+s0==>s0=3s1
可得:s2+s1=3s1=s0 在SΔBRC中:SΔBRQ==SΔBQC ======> RQ==QC ===========> s0==s3
========>s0=3s1;
=======>s1+s2+s3+s1=7s1=(1/3)s=======>s1=(1/21)/s==========>s0=(1/7)s;
证明普通:

如图所示作AG∥BC交BE延长线于点G,作DH∥AB交CF于点H,
则得:AG:BC=AE:EC=1:2,AP:PD=AG:BD=3:4 *****************(1)
又由于DH:BF=1:3,DH:AF=1:6,
所以DR:AR=1:6,DR:DA=1:7, ********************************(2)
/****************************************************************************************************
PS:到了此处如果,不追究严格的论证方法,应该可以直接看出:SΔDRC=1/7h*i/3BC:SΔBFC=BC*1/3h=1:7;
S△CDR=1/7S△BFC=1/21S△ABC,
因此S△PQR:S△ABC=1:7 即:S△PQR=1/7S△ABC=1/7
/*****************************************************************************************************
下面还是给出严格的证明过程:
由(1)(2)有AP:PR = 3 :3 即 P为AR的中点。
同理可得Q为BP中点,R为CQ中点。
连接AQ、CP、BR。
在△AQR中,P为AR中点,所以由同底等高得S△AQP=S△RQP
同理有S△PQR=S△BQR=S△CPR=S△AQR **************************(3)
因为F、D、E分别为三角形三条边的三等分点
所以S△ABE=S△CBF=S△ADC=1/3*S△ABC (底在同一条线上,高相等)
所以S△ABE+S△CBF+S△ADC=S△ABC ****************************(4)
而(4)中三个小三角形△BFQ、△AEP、△CDR加了两次,但是△PQR没有加
所以△BFQ + △AEP + △CDR = △PQR ******************************(5)
而在△BRC中DC : BC = 1 :3
得到S△CDR :S△BCR= 1 :3
同理S△BFQ :S△BAQ=1 :3
S△AEP :S△ACP= 1 :3
所以由(5)有S△BAQ + S△ACP + S△BCR = 3*(△BFQ + △AEP + △CDR)
=3*S △PQR ***********************(6)
由(3)(6)得到S△PQR=1/7S△ABC
#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <cstdlib> #include <iomanip> #include <cmath> #include <ctime> #include <map> #include <set> using namespace std; #define lowbit(x) (x&(-x)) #define max(x,y) (x>y?x:y) #define min(x,y) (x<y?x:y) #define MAX 100000000000000000 #define MOD 1000000007 #define pi acos(-1.0) #define ei exp(1) #define PI 3.141592653589793238462 #define ios() ios::sync_with_stdio(false) #define INF 0x3f3f3f3f #define mem(a) (memset(a,0,sizeof(a))) typedef long long ll; int t; struct point { double x; double y; }node[4]; double area(point a,point b,point c) { return fabs((b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y)); } int main() { scanf("%d",&t); while(t--) { for(int i=0;i<=2;i++) { scanf("%lf%lf",&node[i].x,&node[i].y); } printf("%.0lf ",area(node[0],node[1],node[2])/(2*7)); } } /* 2 3994.707 9251.677 4152.916 7157.810 5156.835 2551.972 6903.233 3540.932 5171.382 3708.015 213.959 2519.852 */