[POI2017]Flappy Bird-bzoj4723

题目描述

《飞扬的小鸟》是一款风靡的小游戏。
在游戏中，小鸟一开始位于(0,0)处，它的目标是飞到横坐标为X的某个位置上。
每一秒，你可以选择点击屏幕，那么小鸟会从(x,y)飞到(x+1,y+1)，或者不点击，那么小鸟会飞到(x+1,y-1)。
在游戏中还有n个障碍物，用三元组(x[i],a[i],b[i])描述，表示在直线x=x[i]上，y<=a[i]或者y>=b[i]的部分都是障碍物，碰到或者擦边都算游戏失败。
请求出小鸟从(0,0)飞到目的地最少需要点击多少次屏幕。

输入格式

第一行包含两个整数n(0<=n<=500000),X(1<=n<=10^9)。
接下来n行，每行三个整数x[i],a[i],bi。
数据保证x[i]<x[i+1]。

第一眼：dp or dfs???
第二眼：哇这个数据范围死人了
...........
横纵坐标之间好像有关系????

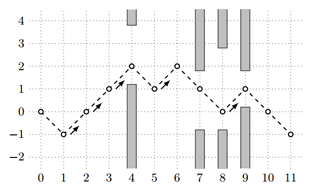
如图,横坐标和纵坐标一定是同奇/偶
走过最后一个柱子后也不需要再跳
考虑横纵坐标的关系,判断能否跳过去
即从现在这个点开始一直下降/上升所能到达的区间能否通过下一个柱子
代码:

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=500005;
int x[maxn],a[maxn],b[maxn];
int main()
{
	int n,l=0,r=0,X;
	scanf("%d %d",&n,&X);
	for(int i=1; i<=n; i++) {
		scanf("%d %d %d",&x[i],&a[i],&b[i]);
		a[i]++;
		b[i]--;
	}
	for(int i=1; i<=n; i++) {
		int dis=x[i]-x[i-1];
		l=max(l-dis,a[i]);
		r=min(r+dis,b[i]);
		if((l+x[i])&1) l++;
		if((r+x[i])&1) r--;
		if(l>r) {
			printf("NIE
");
			return 0;
		}
	}
	printf("%d
",(l+x[n])>>1);
	return 0;
}