Problem A. Ascending Rating
题意:
给出一个序列的前k项,后面的n-k+1项可由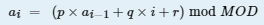 推出,定义一个区间的maxrating为区间的最大值,count为区间最大值的变换次数,给定子区间的长度m,求
推出,定义一个区间的maxrating为区间的最大值,count为区间最大值的变换次数,给定子区间的长度m,求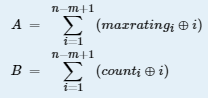
分析:
首先求区间最大值,这是单调队列的经典问题就不用说了。对于变换次数,考虑维护单调递增序列或者维护单调递减序列,但是仔细一想好像都不对,因为我们在抛出之前区间的点时,会对之后的区间造成影响。如果反过来想一下,我们从后开始循环,维护一个单调递减序列,单调队列中元素个数就是变换次数,考虑区间变换时抛出超过区间范围的点,而右边的点对左边的点是没有影响的,所以我们就完美的解决了这个问题。做过很多这种要反着想的题,但是一比赛就不会,哇的一下就哭出来了.jpg。
代码:

#include <map> #include <queue> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int maxn=7e7+100; int a[maxn]; int que[maxn],maxval[maxn],cnt[maxn]; void getMax(int n,int k) { int head=0,rear=0; for(int i=1;i<=n;i++){ while(rear>head&&a[que[rear-1]]<=a[i]) rear--; que[rear++]=i; if(i<k) continue; while(que[head]<i-k+1) head++; maxval[i]=a[que[head]]; } } void getCnt(int n,int k) { int head=0,rear=0; for(int i=n;i>=1;i--){ while(rear>head&&a[que[rear-1]]<=a[i]) rear--; que[rear++]=i; if(i>n-k+1) continue; while(que[head]>i+k-1) head++; // cout<<i+k-1<<" "<<head<<" "<<rear<<endl; cnt[i+k-1]=rear-head; } } int main() { // freopen("in.txt","r",stdin); int T,n,m,k,p,q,r,mod; scanf("%d",&T); while(T--) { scanf("%d%d%d%d%d%d%d",&n,&m,&k,&p,&q,&r,&mod); for(int i=1;i<=k;i++){ scanf("%d",&a[i]); } for(int i=k+1;i<=n;i++){ a[i]=((ll)p%mod*a[i-1]%mod+(ll)q%mod*i%mod+r%mod)%mod; } getMax(n,m); getCnt(n,m); ll sum1=0,sum2=0; for(int i=m;i<=n;i++){ // cout<<i<<" "<<maxval[i]<<" "<<cnt[i]<<endl; sum1+=maxval[i]^(i-m+1); sum2+=cnt[i]^(i-m+1); } printf("%lld %lld ",sum1,sum2); } return 0; }
Problem C. Dynamic Graph Matching
题意:
定义一个图的匹配为没有公共顶点的边的集合。+ u v表示在u,v顶点之间连一条边,- u v表示去掉u,v顶点之间的一条边。问图的匹配数分别为1,2……n/2时(集合中边的数量),对应有多少种拿法?
分析:
我的理解是用二进制中的每一位代表一个顶点,为1则代表相应的顶点被选。
dp【i】表示i的二进制中为1的位对应的顶点被选的情况下,一共有多少种方案数。
当添加一条边时,所有同时包含u,v两个顶点的状态s需要更新,dp【s】+=dp【s-u-v】,同理当删除一条边时,dp【s】-=dp【s-u-v】。
更新dp【i】时,相应的答案也需要进行更新,ans【bit【i】】+=(-=)dp【s-u-v】(bit【i】表示i的二进制中有几个1)。
参考资料:大佬博客(以上为对大佬思路的理解)
代码:

#include <map> #include <queue> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int mod=1e9+7; const int maxn=1<<11; char op; int n,m,T; int bit[maxn]; ll dp[maxn],ans[11]; //计算x的二进制中有多少1 int calc(int x) { int cnt=0; while(x) { cnt++; x-=(x&-x); } return cnt; } void init() { for(int i=1;i<(1<<10);i++){ bit[i]=calc(i); } } int main() { // freopen("in.txt","r",stdin); init(); scanf("%d",&T); while(T--) { cls(dp); cls(ans); dp[0]=1; scanf("%d%d",&n,&m); while(m--){ int u,v,sign; scanf(" %c %d%d",&op,&u,&v); //第1个点的状态用二进制表示为00000000001 //第2个点的状态用二进制表示为00000000010 //…… //所以在这里手动减1 u--,v--; if(op=='+') sign=1; else sign=-1; for(int i=1;i<(1<<n);i++){ //i&(1<<u)如果不为0,则代表在第u位都为1,即i包括u顶点 if((i&(1<<u))&&(i&(1<<v))){ //如果添加一条边,加上增加的方案数,否则减 dp[i]+=sign*dp[i-(1<<u)-(1<<v)]; //考虑更新时对答案的贡献 ans[bit[i]]+=sign*dp[i-(1<<u)-(1<<v)]; dp[i]=(dp[i]%mod+mod)%mod; ans[bit[i]]=(ans[bit[i]]%mod+mod)%mod; } } for(int i=2;i<=n;i+=2){ printf("%lld%c",ans[i],(i==n?' ':' ')); } } } return 0; }
Problem D. Euler Function
题意:
找到第k小的正数,对于euler(n)的值为合数的集合。
分析:
看了大佬们3分钟就ac了,我就懂了,打表之后发现只有当n=1,2,3,4,6时,euler(n)不是合数。
代码:

#include <map> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int maxn=1e5; int main() { // freopen("in.txt","r",stdin); int k,T,ans; scanf("%d",&T); while(T--) { scanf("%d",&k); if(k==1) ans=5; else ans=k+5; printf("%d ",ans); } return 0; }
Problem F. Grab The Tree
题意:
给出一颗树,Q能够拿图中任意数量点,但是需要保证拿的点中任意两点没有边相连,T拿Q拿后剩下的点,定义每个人的分数为所拿的点的异或值,分数大的赢。
分析:
当时想的是如果所有点的异或值不为0,那么肯定二进制中为1的位对应的顶点有奇数个,考虑只拿一个最高位对应的顶点,则Q的分数一定比T高。否则,如果异或值
为0,则Q的所有点^T的所有点=0,即Q的异或值等于T的异或值。
代码:

#include <map> #include <queue> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int mod=1e9+7; const int maxn=1<<11; int main() { // freopen("in.txt","r",stdin); int n,T; scanf("%d",&T); while(T--) { int XOR; scanf("%d",&n); for(int i=1;i<=n;i++){ int p; scanf("%d",&p); if(i==1) XOR=p; else XOR^=p; } for(int i=1;i<n;i++){ int u,v; scanf("%d%d",&u,&v); } if(XOR) printf("Q "); else printf("D "); } return 0; }
Problem L. Visual Cube
题意:
画立方体。
分析:
模拟就好了。
代码:

#include <map> #include <math.h> #include <string> #include <stdio.h> #include <string.h> #include <iostream> #include <algorithm> using namespace std; #define ll long long #define ull unsigned long long #define cls(x) memset(x,0,sizeof(x)) #define clslow(x) memset(x,-1,sizeof(x)) const int maxn=1e3; char rect[maxn][maxn]; void print(int n,int m) { for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ printf("%c",rect[i][j]); } printf(" "); } } int main() { // freopen("in.txt","r",stdin); int l,w,h,T; scanf("%d",&T); while(T--) { scanf("%d%d%d",&l,&w,&h); int rest=2*w; int n=rest+h*2+1,m=rest+l*2+1; //左上 for(int i=1;i<=rest;i++){ for(int j=1;j<=rest-i+1;j++){ rect[i][j]='.'; } } //上面 int cnt=0; for(int i=1;i<=rest;i++){ char lch,rch; if(i&1) lch='+',rch='-'; else lch='/',rch='.'; bool flag=true; for(int j=rest-i+2;j<=m-cnt;j++){ if(flag) rect[i][j]=lch; else rect[i][j]=rch; flag=!flag; } cnt++; } //正面 for(int i=rest+1;i<=n;i++){ char lch,rch; if(i&1) lch='+',rch='-'; else lch='|',rch='.'; bool flag=true; for(int j=1;j<=2*l+1;j++){ if(flag) rect[i][j]=lch; else rect[i][j]=rch; flag=!flag; } cnt++; } //右面 cnt=0; for(int i=1;i<=n;i++){ int last; char pre,now; if(i<=rest) last=m-cnt; else last=2*l+1; pre=rect[i][last]; for(int j=last+1;j<=m;j++){ if(pre=='/') now='|'; else if(pre=='|') now='/'; else if(pre=='+') now='.'; else if(pre=='.') now='+'; rect[i][j]=now; pre=now; } cnt++; } //右下 cnt=0; for(int i=n-rest+1;i<=n;i++){ for(int j=m-cnt;j<=m;j++){ rect[i][j]='.'; } cnt++; } print(n,m); } return 0; }
