程序设计入门-C语言基础知识-翁恺-第三周：循环-详细笔记（三）

第三周：循环

目录

• 第三周：循环
  • 3.1 循环
  • 3.2 循环计算
  • 3.3 课后习题
  • 3.4 讨论题（不需要掌握）

3.1 循环

while循环
语法：
while(条件表达式){
//循环体语句
}

• 如果我们把while翻译作“当”，那么一个while循环的意思就是：当条件满足时，不断地重复循环体内的语句。
• 循环体执行之前判断是否继续循环，所以有可能循环一次也没有被执行、
• 条件成立时循环继续的条件
• 循环体执行步骤
  1. 检查条件表达式是否成立
  2. 不成立结束循环，成立执行循环体内语句后回到第一步。

例子：数整数的位数
用户输入一个整数，要求输出整数的位数。比如输入123，输出3

输入样例
123

输出样例
3

程序实现：

#include <stdio.h>

int main(int argc, char *argv[]) {

	
	
 int x = 0;
 int n = 0;
	
 printf("请输入一个整数：");
 scanf("%d", &x);
 n++;
 x /= 10;
 while(x > 0) {
  x /= 10;
  n++;
 }
	
 printf("这个整数的位数是%d", n);
  
 return 0;
}

运行结果：

请输入一个整数：123
这个整数的位数是3

复合运算

• 5个算术运算符，+、-、、/、% 都可以和赋值运算符"="结合起来，形成复合运算符：“+=”、“-=”、“=”、“/=”、“%=”
  • total += 5;
  • total = total + 5;
• 注意两个运算符中间不要有空格

递增递减运算符

• "++"和"--"是两个很特殊的运算符，它们是单目运算符，这个算子还必须是变量。
• 以上两个运算符分别叫做递增和递减运算符，它们的作用就是给这个变量+1或者-1
  • count ++；
  • count += 1;
  • count = count + 1;
  • 以上3个表达式是等价的
    前缀和后缀
• ++和--可以放在变量的前面，叫做前缀形式，也可以放在变量的后面，叫做后缀形式。
• a++的值是先将a参与运算，再将a的值自增1，而++a则是先将a的值自增1再参与运算。
• 递减运算符同理

比如：

int a = 0;
int b = a++ ; // a = 1，b = 0，
int c = ++a; // a = 2 ，c = 2

do-while循环

• 在进入循环体的时候不做条件表达式的检查，而是在执行完一轮循环体的代码之后，再来检查循环的条件是否满足，如果满足则进行下一轮循环，不满足则结束循环。
• 注意do-while的结尾需要分号的
• do-while和while循环区别是前者先执行语句再判断条件，而后者先判断条件再执行语句，具体使用那种循环需要根据实际情况而定。
  语法：
  do
  {
  <循环体语句>
  } while(<循环条件>);

3.2 循环计算

猜数游戏

• 让计算机来想一个数，然后让用户来猜，用户每输入一个数，就告诉他打了还是小了，直到用户猜中为止，最后还要告诉用户它猜了多少次。

程序实现分析：

1. 计算机随机想一个数，记在变量number里;
2. 一个负责记次数的变量count初始化为0
3. 让用户输入一个数字a
4. count递增（加1）
5. 判断a和number的大小关系，如果a大，就输出“大”；如果a小就输出“小”；
6. 如果a和number是不相等的（无论大还是小），程序转回到第3步；
7. 否则，程序输出“猜中”和次数，然后结束。

程序实现：

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(int argc, char *argv[]) {
	
 srand(time(0));
 int number = rand() % 100 + 1;
 int count = 0;
 int a = 0;
	
 printf("我已经想好了一个1到100之间的数。");
 do{
  printf("请猜这个1到100之间的数：");
  scanf("%d", &a) ;
  count ++;
  if( a > number){
   printf("你猜的数大了。");
  } else if(a < number){
   printf("你猜的数小了。");
  }
 } while (a != number);
	
 printf("太好了，你用了%d次就猜到了答案。
", count);
 return 0;
}

测试样例：

我已经想好了一个1到100之间的数。请猜这个1到100之间的数：50
你猜的数大了。请猜这个1到100之间的数：25
你猜的数大了。请猜这个1到100之间的数：13
你猜的数小了。请猜这个1到100之间的数：19
你猜的数大了。请猜这个1到100之间的数：16
你猜的数大了。请猜这个1到100之间的数：15
太好了，你用了6次就猜到了答案。

tips:在7次内一定能猜到答案，详见讨论题

3.3 课后习题

1、 题目内容：
你的程序要读入一系列正整数数据，输入-1 表示输入结束，-1 本身不是输入的数据。程
序输出读到的数据中的奇数和偶数的个数。
输入格式:
一系列正整数，整数的范围是（0,100000）。如果输入-1 则表示输入结束。

输出格式：
两个整数，第一个整数表示读入数据中的奇数的个数，第二个整数表示读入数据中的偶数的
个数。两个整数之间以空格分隔。

输入样例：
9 3 4 2 5 7 -1

输出样例：
4 2

算法分析：

1. 读取用户输入一个数记录在变量number中
2. 判断number是奇数或者偶数还是-1（能被2整除的数就是偶数，反之就是奇数）
   2-1. 如果是-1，程序继续执行第3步
   2-2. 如果用户输入数字超出范围，提示用户重新输入，程序回到第1步
   2-3. 如果是奇数记录在变量odd中，并自增1，程序回到第1步
   2-4. 如果是偶数记录在变量even中，并自增1，程序回到第1步
3. 输出奇数和偶数，程序结束

程序实现：

#include <stdio.h>

int main(int argc, char *argv[]) {
 int number = 0;
 int odd = 0;
 int even = 0;
	
 printf("请输入一系列整数范围在0-100000，输入-1表示结束输入：");
 scanf("%d", &number);
 while(number != -1) {  
  if(number < 0 || number > 100000){ //"||"表示 在"||"左边表达式或者右边的表达式任意一个成立，也就是说当number<0 或者 number>100000 时表达式成立 
   printf("您输入的数字%d，超出范围，不会被统计。
", number);
  } else if (number % 2 == 0){
   even++;
  } else {
   odd++;
  }
  scanf("%d", &number);
 }
 printf("%d %d", odd, even);
}

//odd 2 
//even 4
//9 3 4 2 5 7 -1
//4 2

测试样例：

请输入一系列整数范围在0-100000，输入-1表示结束输入：9 3 4 2 5 7 -1
4 2
--------------------------------

请输入一系列整数范围在0-100000，输入-1表示结束输入：9 3 4 2 5 7 -2 110000 -1
您输入的数字-2，超出范围，不会被统计。
您输入的数字110000，超出范围，不会被统计。
4 2
--------------------------------

2、 题目内容：

对数字求特征值是常用的编码算法，奇偶特征是一种简单的特征值。对于一个整数，从个位
开始对每一位数字编号，个位是 1 号，十位是 2 号，以此类推。这个整数在第 n 位上的数
字记作 x，如果 x 和 n 的奇偶性相同，则记下一个 1，否则记下一个 0。按照整数的顺序把
对应位的表示奇偶性的0和1都记录下来，就形成了一个二进制数字。比如，对于342315，
这个二进制数字就是 001101。
这里的计算可以用下面的表格来表示：

按照二进制位值将 1 的位的位值加起来就得到了结果 13。
你的程序要读入一个非负整数，整数的范围是[0,1000000]，然后按照上述算法计算出表
示奇偶性的那个二进制数字，输出它对应的十进制值。
提示：将整数从右向左分解，数位每次加 1，而二进制值每次乘 2。

输入格式:
一个非负整数，整数的范围是[0,1000000]。

输出格式：
一个整数，表示计算结果。

输入样例：
342315

输出样例：
13

算法分析：

1. 读取用户输入的数字记录到number
2. 判断用户输入的值，超出范围，提示用户，程序回到第1步
3. 否则在合理范围内求number的特征值
   3-1. 如果number为0，程序跳转第4步
   3-2. 当前的位数digit自增1
   3-3. 取number的个位到tmp中
   3-4. 分别取tmp和digit的奇偶性记录到isEvenTmp和isEvenDigit中
   3-5. 如果tmp和digit的奇偶性相同，累加2当前的平方数squareOfTwo到eigenvalue中
   3-6. 将number整除10，移除掉已经处理的位数，squareOfTwo乘2得到下一个平方数，程序回到第3-1
4. 输出特征值eigenvalue，程序结束

tips：有一种特殊情况用户第一次输入的number就是0，那么我们的程序会在3-1跳转到第4步结束，并不会计算特征值，我们知道0的特征值为0，因此我们只需要将eigenvalue的默认值设置为0即可。当然还有别的处理方法，具体使用哪种我们需要考量程序的可读性和效率择优选择。你是否能想出其他的处理方式呢？

程序实现:

#include <stdio.h>

int main(int argc, char *argv[]) {
 int number = 0;
 int digit = 0;
 int tmp = 0;
 int eigenvalue = 0;
 int isEvenTmp = 0;
 int isEvenDigit = 0;
 int squareOfTwo = 1; //2的0次方为1 
	
 printf("请输入一个整数范围在0-1000000：");
 scanf("%d", &number);
 while(number < 0 || number > 1000000 ) {
  printf("%d已超出范围，请重新输入：", number);
  scanf("%d", &number); 
 }
	
 while(number != 0){
  digit++;
  tmp = number % 10;
  isEvenTmp = tmp % 2 == 0;
  isEvenDigit = digit % 2 == 0;
  if(isEvenTmp == isEvenDigit){
   eigenvalue += squareOfTwo;
  }
  number /= 10;
  squareOfTwo *= 2; 
 }
	
 printf("%d", eigenvalue);
 return 0;
}

测试样例：

请输入一个整数范围在0-1000000：342315
13
--------------------------------

请输入一个整数范围在0-1000000：0
0
--------------------------------

请输入一个整数范围在0-1000000：12345
31
--------------------------------

请输入一个整数范围在0-1000000：-1
-1已超出范围，请重新输入：1100000
1100000已超出范围，请重新输入：123
7
--------------------------------

3.4 讨论题（不需要掌握）

三、(3-2 循环计算)
标题：猜数游戏
内容：为什么方法正确的话，100 以内的数最多猜 7 次就够了？
题目分析：
当我们知道一个数的范围时，我们可以采取二分法来猜这个数字的大小：

1. 猜这个范围的中间值
   2.程序反馈数字是否猜对
   2-1. 如果不对程序会告诉我们大小，就能把范围会缩小一半然后回到第1步
   2-2. 否则我们猜对了

我们先小范围测试，把范围缩小到1-10

tips:

• 在最坏的情况下我们使用二分法了4次猜出正确的数字
• 在第一次猜5，也可能是大的情况，范围则为[1,4]有4个数字，但是我们要求每次都是最坏的情况因此取小的情况范围[6,10]
• mid：用户猜的中间数字
• com: num和实际数字之间的关系，E=相等，B=大了，S=小了
• ran: 缩小后的范围 比如[4-8]代表4、5、6、7、8
• count: 范围内的整数个数
• time: 用户猜了多少次
• 变量star代表范围起始，变量end代表范围结束。
• 中间数mid的计算公式：mid = star + (end - star + 1)/2;
• 缩小的范围range计算公式：
  • 当用户猜的数大了的情况，end = mid- 1; ran = [star,end];
  • 当用户猜的数小了的情况，star = mid + 1; ran =[star,end];
• rang整数个数count的计算公式： count = (end - star + 1);

那么采用二分法最坏的情况下需要多少次能猜中100呢？
假设我们有n个连续的整数，它的范围为[1,n]
如果我们采取从递增猜方法从1开始猜一直猜到n，1、2、..n 那么最坏的情况下我们就需要猜n次。
对于100个数来说就是要猜100次。

但是我们用了二分法，如果是最坏的情况，我们的范围中整数的个数每次都会缩小一半，n/2^1、n/22...n/2^m，
当n除以2的m次幂等于1时我们就能猜出程序的那个数字了，也就是说理论上我们需要猜m次。
因此如果有n个数，计算猜m次的公式是m=log2n; m是以2为底n的对数。
通过计算log2100 = 6.6438561898，我们知道理论最多猜7次就能得到正确答案。

这里用连续猜和二分法猜数的效率差了大约只有10倍，当这个数字的范围是1到100万时，连续猜需要猜100万次，而二分法只需要猜20次，足足差了5万倍，如果这个猜数也是由一个程序来完成，A程序使用递增猜算法(n)，B程序使用二分猜算法(log2n)，当n等于100万时他们的效率就差了5万倍，可以预见当n增加复杂度还会以几何式的增加， 由此可见一个好的算法往往会给程序带来效率的是数量级上的提升。

扩展：理论次数和实际次数

细心的读者会发现通过上面公式计算所得的理论次数和实际次数在一些情况下会不一样。比如说当范围为[1,8]时最多应该猜多少次呢？通过计算我们知道是3，但是这个结果对吗？我们通过表格来模拟一下程序。
范围[1,8] 程序模拟：

结果是4次，我们确实在第3次知道了结果，但是需要猜第4次程序才会告诉我们猜对了。因此实际猜的次数 rm = log2n + 1;
如果我们要猜的整数恰好是7的话，我们算出来的结果是 3次（舍去了log2n小数的部分，比如2.99 舍掉小数部分就是2）,模拟下程序的结果是否和我们理论计算的一致

范围[1,7] 表格模拟：

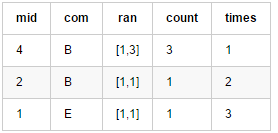
确实是3次

范围[1,6]：

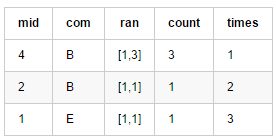
范围[1,5]：

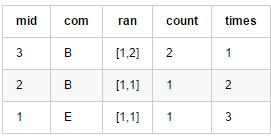
范围[1,4]：

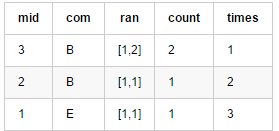
扩展-思考：
你能用实现模拟猜数程序吗？