-------------------siwuxie095
图的表示
这里介绍图的表示方式,那么什么样的数据结构,才能
真正的表示一个图?
其实图的表示方式非常简单,大家只需要抓住图的核心
即可,而对于图来说,它的核心其实就是顶点和边
通常使用两种不同的方式来表示图,对于这两种不同的
表示方式,它们的实质其实是:对于边的表示,应该采
用哪种数据结构
邻接矩阵
第一种表示方式叫做邻接矩阵(Adjacency Matrix),即 使用
一个二维矩阵,来表示一张图
(1)对于无向图来说,看如下实例:

这张图一共有 4 个顶点和 4 条边,可以使用一个二维矩阵来表示

如果有 n 个顶点,就一共有 n 行 n 列,如果称这个矩阵为 A,
则 A[i][j] 就表示是 i、j 这两个顶点是否相连,这里用 0 表示不
相连,1 表示相连
「也可以使用一个布尔值来表示是否相连」
在使用邻接矩阵表示无向图时,沿主对角线对称,
即 A[i][j] = A[j][i]
(2)对于有向图来说,看如下实例:
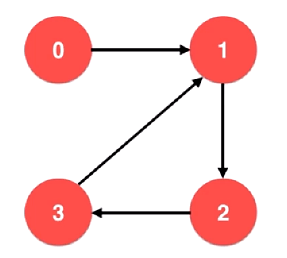
这张图一共有 4 个顶点和 4 条边,可以使用一个二维矩阵来表示
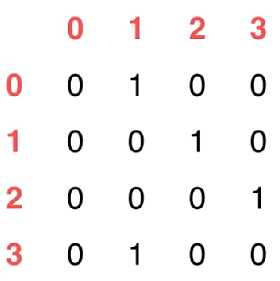
从 0 到 1 有一条边,所以 A[0][1] 为 1,而从 1 到 0 没有边,
所以 A[1][0] 为 0 … 以此类推
总而言之,邻接矩阵的每一行都表示当前顶点与图中所有顶点
之间的边的信息
邻接表
第二种表示方式叫做邻接表(Adjacency Lists),和邻接矩阵不同,
邻接表的每一行,只表示和当前顶点相连接的顶点的信息
(1)对于无向图来说,看如下实例:

不难看出,在邻接表的表示方式中,每一行都相当于一个链表,存放了
和当前顶点相邻的所有顶点
(2)对于有向图来说,看如下实例:

显然,邻接表这种表示方式,在存储空间上,它会比邻接矩阵所使用的
存储空间要小,但这也不代表邻接矩阵是没有用的
事实上,对于一个问题,如果要使用图的方式来建模,究竟是选择邻接
矩阵还是选择邻接表来表示图,应该具体问题,具体分析
总体原则:
1)邻接表适合表示稀疏图(Sparse Graph)
2)邻接矩阵适合表示稠密图(Dense Graph)
那么什么是稀疏图,什么是稠密图呢?
简单来说:
1)如果图中的边相对比较少,就可以叫稀疏图
2)如果图中的边相对比较多,就可以叫稠密图
什么是多,什么是少,依然比较抽象,看如下实例:

从直观上来看,第一感觉这是稠密图,但实际上,它更应该被划分为
稀疏图,因为每一个顶点最多只有不超过 8 条邻边,但在最大的情况
下,每一个顶点应该能和其它所有顶点都有一条边
显然,该图中边的个数远远的小于其所能拥有的最大的边的个数
再看如下实例:

上图就是稠密图的一个最典型的情况 --- 完全图
所谓完全图,即 图中任意两个顶点之间都有边
事实上,在解决实际问题时,很多情况下都要使用完全图
如:要做一个电影推荐的网站,要想推荐电影,就要找到和一部电影
相似的所有电影。为了计算相似性,很多时候都是计算出每一部电影
和其它所有电影之间的相似度
程序:
SparseGraph.h:
#ifndef SPARSEGRAPH_H #define SPARSEGRAPH_H
#include <iostream> #include <vector> #include <cassert> using namespace std;
// 稀疏图 - 邻接表 class SparseGraph {
private:
int n, m; //n 和 m 分别表示顶点数和边数 bool directed; //directed表示是有向图还是无向图 vector<vector<int>> g; //g[i]里存储的就是和顶点i相邻的所有顶点
public:
SparseGraph(int n, bool directed) { //初始化时,有n个顶点,0条边 this->n = n; this->m = 0; this->directed = directed; //g[i]初始化为空的vector for (int i = 0; i < n; i++) { g.push_back(vector<int>()); } }
~SparseGraph() {
}
int V(){ return n; } int E(){ return m; }
//在顶点v和顶点w之间建立一条边 void addEdge(int v, int w) {
assert(v >= 0 && v < n); assert(w >= 0 && w < n);
g[v].push_back(w); //(1)顶点v不等于顶点w,即 不是自环边 //(2)且不是有向图,即 是无向图 if (v != w && !directed) { g[w].push_back(v); }
m++; }
//hasEdge()判断顶点v和顶点w之间是否有边 //hasEdge()的时间复杂度:O(n) bool hasEdge(int v, int w) {
assert(v >= 0 && v < n); assert(w >= 0 && w < n);
for (int i = 0; i < g[v].size(); i++) { if (g[v][i] == w) { return true; } }
return false; } };
//事实上,平行边的问题,就是邻接表的一个缺点 // //如果要在addEdge()中判断hasEdge(),因为hasEdge()是O(n)的复 //杂度,那么addEdge()也就变成O(n)的复杂度了 // //由于在使用邻接表表示稀疏图时,取消平行边(即 在addEdge() //中加上hasEdge()),相应的成本比较高 // //所以,通常情况下,在addEdge()函数中就先不管平行边的问题, //也就是允许有平行边。如果真的要让图中没有平行边,就在所有 //边都添加进来之后,再进行一次综合的处理,将平行边删除掉
#endif |
DenseGraph.h:
#ifndef DENSEGRAPH_H #define DENSEGRAPH_H
#include <iostream> #include <vector> #include <cassert> using namespace std;
// 稠密图 - 邻接矩阵 class DenseGraph {
private:
int n, m; //n 和 m 分别表示顶点数和边数 bool directed; //directed表示是有向图还是无向图 vector<vector<bool>> g; //二维矩阵,存放布尔值,表示是否有边
public:
DenseGraph(int n, bool directed) { //初始化时,有n个顶点,0条边 this->n = n; this->m = 0; this->directed = directed; //二维矩阵:n行n列,全部初始化为false for (int i = 0; i < n; i++) { g.push_back(vector<bool>(n, false)); } }
~DenseGraph() {
}
int V(){ return n; } int E(){ return m; }
//在顶点v和顶点w之间建立一条边 void addEdge(int v, int w) {
assert(v >= 0 && v < n); assert(w >= 0 && w < n);
//如果顶点v和顶点w之间已经存在一条边, //则直接返回,即排除了平行边 if (hasEdge(v, w)) { return; }
g[v][w] = true; //如果是无向图,则g[w][v]处也设为true(无向图沿主对角线对称) if (!directed) { g[w][v] = true; }
m++; }
//hasEdge()判断顶点v和顶点w之间是否有边 //hasEdge()的时间复杂度:O(1) bool hasEdge(int v, int w) { assert(v >= 0 && v < n); assert(w >= 0 && w < n); return g[v][w]; } };
//addEdge()函数隐含着:当使用邻接矩阵表示稠密图时,已经 //不自觉的将平行边给去掉了,即 在添加边时,如果发现已经 //存在该边,就不做任何操作,直接返回即可 // //事实上,这也是使用邻接矩阵的一个优势可以非常方便的处理 //平行边的问题 // //另外,由于使用的是邻接矩阵,可以非常快速的用O(1)的方式, //来判断顶点v和顶点w之间是否有边
#endif |
【made by siwuxie095】