1、公式法推导
- 已知数据集 (X,Y),X、Y 均为列向量,列内第 i 行代表 X、Y 的一个样本 xi、yi
- 假设 X 和 Y 满足线性映射:Y=WTX
- 则预测值与真实值之间的误差(距离)为
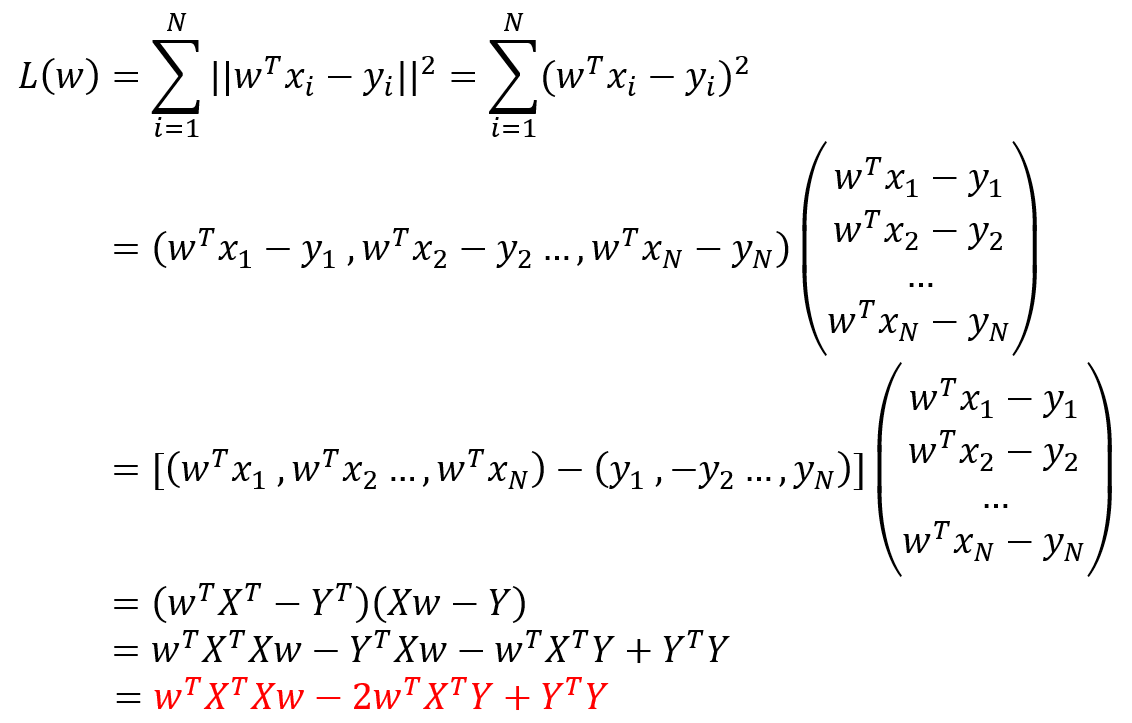
-
- PS:因为 YTXw 是一个实数,因此 YTXw =wTXTY
- 则权重矩阵 w 的最小二乘估计值
 为:
为:
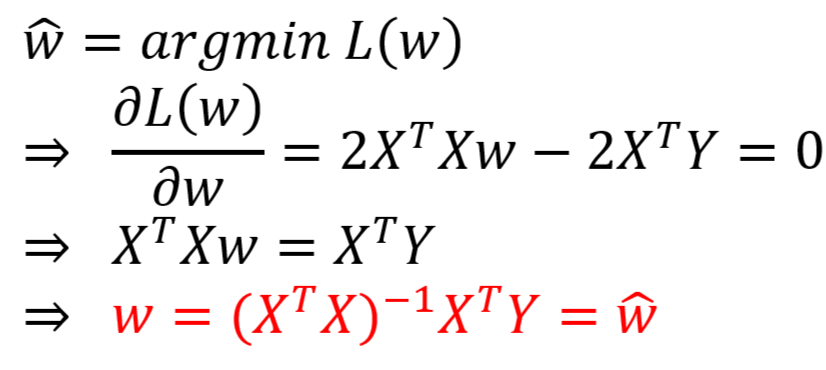
2、几何法推导
- 假设
- X,Y 是高维向量(维度大于2)
- 预测空间
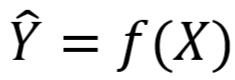 为二维空间,即预测函数将高维向量 X 映射到二维空间
为二维空间,即预测函数将高维向量 X 映射到二维空间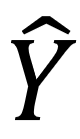 如下图,
如下图, 为真实标签向量,
为真实标签向量,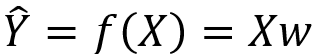 为预测标签向量,
为预测标签向量,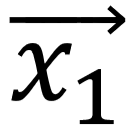 和
和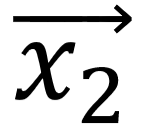 是二维预测空间的坐标轴,
是二维预测空间的坐标轴, 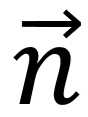 为垂直于映射空间且与高维标签向量相交的法向量(由图可知
为垂直于映射空间且与高维标签向量相交的法向量(由图可知 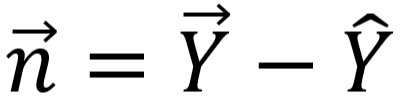 )
)
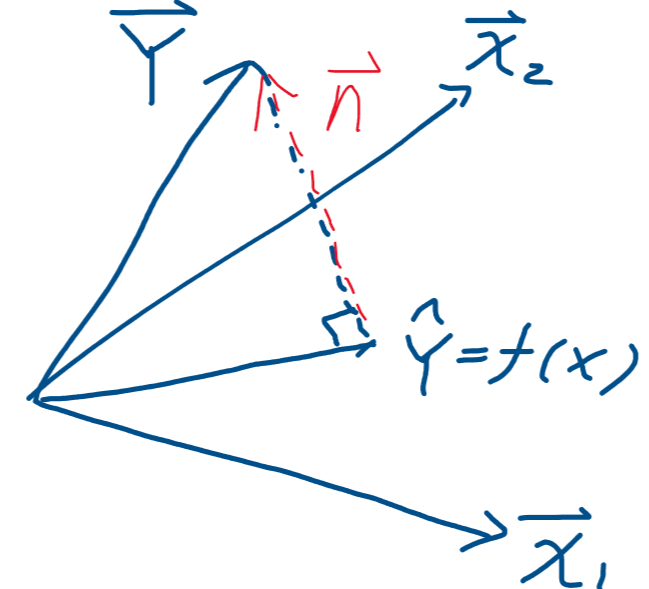
- 如上图,法向量
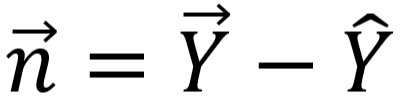
- 因为
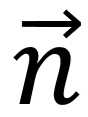 与 X 各个坐标轴均垂直,所以有:
与 X 各个坐标轴均垂直,所以有:

- 由上推导可知,最小二乘法的几何意义在于,通过使(“标签向量“ 与 ”预测空间坐标轴向量“之间的总距离)最小化,得出一个参数为 w 的映射函数,将特征为 X 的目标向量 Y 映射为预测空间的预测向量
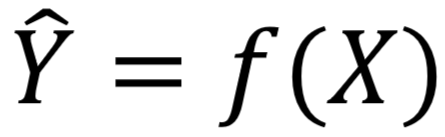
3、概率角度推导
- 已知数据集(X,Y)
- 假设:
- 映射函数为 f(w)=wTx
- 真实标签与预测值之间的关系为:y=f(w)+ε=wTx+ε
- 其中 ε~N(0,σ2)
- 由上述假设可知:
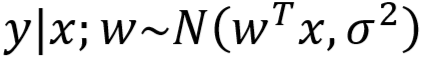
- 即

- 使用极大似然估计(MLE)计算 w 的估计值

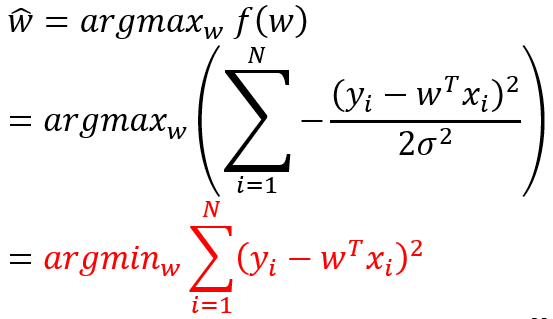
- 上述求得的
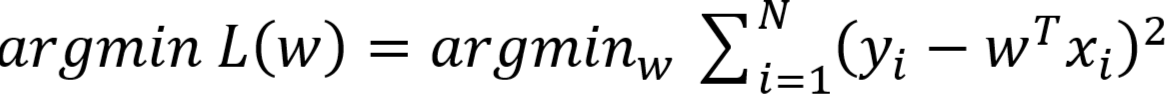 ,就是最开始使用的最小二乘法公式
,就是最开始使用的最小二乘法公式