案例6-1.3 哥尼斯堡的“七桥问题” (25分)--dfs图连通+度判断

 

 

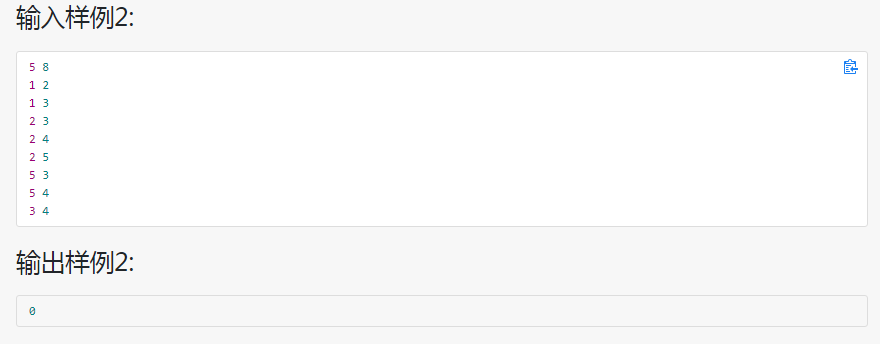
 解题思路：1、判断各结点的度是否是偶数

                        如果是偶数则判断是否是连通图：连通图，则存在欧拉回路，否则，不存在

                       如果是奇数，则不存在欧拉回路

#include <stdio.h>
#include <string.h>
#define MaxVertex 1000+1
int G[MaxVertex][MaxVertex];
int visit[MaxVertex];
int degree[MaxVertex];
int Nv,Ne;
void InitGraph() {//初始化图
    memset(G,0,sizeof(G));
    memset(degree,0,sizeof(degree));
    memset(visit,0,sizeof(visit));
    scanf("%d %d",&Nv,&Ne);
    int i,j,v1,v2;
    for(i=0; i<Ne; i++) {
        scanf("%d %d",&v1,&v2);
        G[v1][v2]=1;
        G[v2][v1]=1;
    }
    for(i=1; i<=Nv; i++) {
        for(j=1; j<=Nv; j++) {
            degree[i]+=G[i][j];
        }
    }

}
int cnt=0;
void dfs(int x) {//连通图
    cnt++;
    visit[x]=1;
    int i;
    for(i=1; i<=Nv; i++) {
        if(!visit[i]&&G[x][i]) {
            dfs(i);
        }
    }
}
int Judge(int degree[]) {//度的奇偶判断
    int i;
    for(i=1; i<=Nv; i++) {
        if(degree[i]%2)
            return 0;
    }
    return 1;
}
int main() {
    InitGraph();
    if(Judge(degree)) {
        dfs(1);
        if(cnt==Nv)
            printf("1");
        else
            printf("0");
    } else
        printf("0");
}