这篇文章提出的FLEX工具,是PrivSQL作者主要参考的工具和实验对比的对象
于是很有必要读一下这篇文章
摘要
现有的差异隐私机制不支持基于SQL的现实分析系统中使用的各种功能和数据库,所以我们提出了弹性敏感性,这是一种用一般的等联接来逼近查询的局部敏感性的新方法。并且证明了弹性敏感度是局部敏感度的上限,因此可以使用任何基于局部敏感度的机制来强制执行差异性隐私。
我们构建了FLEX,是一个端到端系统,可以使用弹性敏感性对SQL查询强制实施差异隐私。并且FLEX与任何现有数据库兼容,可以为实际SQL查询强制实施差异性隐私,性能开销低。
1.介绍
数据分析师已经开始依赖对数据的无限制访问来获得最大的生产力。通常以支持SQL查询的关系数据库的形式提供此访问。当前技术不能为个人提供隐私保护,同时为分析人员提供通用访问权限。
允许组织成员不受限制地访问数据是主要的侵犯隐私的原因。差异隐私允许对数据进行常规统计分析,同时通过强有力的正式隐私保护来保护有关个人的数据,于是使用差异隐私是一个很好的解决方案。用于通用数据分析的差异性隐私仍然是一个开放的话题挑战。(值得突破的点或者领域)
各种机制[14、41-43、45、48]为类似SQL的查询的某些子集提供了不同的隐私。其中
14是J. Blocki, A. Blum, A. Datta, and O. Sheffet. Differentially private data analysis of social networks via restricted sensitivity. In Proceedings of the 4th Conference on Innovations in Theoretical Computer Science, ITCS ’13,pages 87–96, New Y ork, NY , USA, 2013. ACM.
41是F. D. McSherry. Privacy integrated queries: an extensible platform for privacy-preserving data analysis. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of data, pages 19–30. ACM, 2009.
42是P . Mohan, A. Thakurta, E. Shi, D. Song, and D. Culler. Gupt: privacy preserving data analysis made easy. In Proceedings of the 2012 ACM SIGMOD International Conference on Management of Data, pages 349–360. ACM, 2012.
43是A. Narayan and A. Haeberlen. Djoin: differentially private join queries over distributed databases. In Presented as part of the 10th USENIX Symposium on Operating Systems Design and Implementation (OSDI 12), pages 149–162,2012.
45是K. Nissim, S. Raskhodnikova, and A. Smith. Smooth sensitivity and sampling in private data analysis. In Proceedings of the thirty-ninth annual ACM symposium onTheory of computing, pages 75–84. ACM, 2007.
48是D. Proserpio, S. Goldberg, and F. McSherry. Calibrating data to sensitivity in private data analysis: A platform for differentially-private analysis of weighted datasets. PVLDB,7(8):637–648, 2014.
通过对作者引用的文章发现,自己设计某个系统前自己需要阅读大量的文章作为基础,一篇一篇地读文章吧。
此外,尽管对差异性隐私的理论方面进行了广泛的研究,但对于差异性隐私对现实世界查询的定量影响知之甚少。
目前对差异性隐私的理论方面进行了广泛的研究,但对于差异性隐私对现实世界查询的定量影响知之甚少。但是这项工作使用有限的一组查询来表示单个特殊用途的分析任务,例如直方图分析[15]或范围查询[32]。据我们所知,目前尚无任何工作探索用于一般现实查询的差异隐私技术的设计和评估。
15是J. Blocki, A. Datta, and J. Bonneau. Differentially private password frequency lists. In 23nd Annual Network and Distributed System Security Symposium, NDSS 2016, San Diego, California, USA, February 21-24, 2016. The Internet Society, 2016.
32是M. Hay, A. Machanavajjhala, G. Miklau, Y . Chen, and D. Zhang. Principled evaluation of differentially private algorithms using dpbench. In F.Özcan, G. Koutrika, and S. Madden, editors, Proceedings of the 2016 International Conference on Management of Data, SIGMOD Conference 2016, San Francisco, CA, USA, June 26 - July 01, 2016, pages 139–154. ACM, 2016.
本文提出了弹性敏感性,这是一种用于SQL查询的差分隐私的新方法。与现有工作相比,我们的方法与真实数据库系统兼容,支持以标准SQL表示的查询,并且可以轻松集成到现有数据环境中。并且 Uber最近采用了这种方法来为内部数据分析实施差异化隐私 网址 https://medium.com/uber-security-privacy/differential-privacy-open-source-7892c82c42b6
我们已经发布了一个用于计算SQL查询弹性敏感性的开源工具[4],链接如此 Dataflow analysis & differential privacy for SQL queries.
网址如下 http://www.github.com/uber/sql-differential-privacy.
本篇论文的贡献如下
1.我们对现实世界中的SQL查询进行了最大的实证研究,总共有810万个查询。从这些结果我们表明,先前的工作中用于评估差异隐私机制的查询不代表现实世界中的查询。基于这些结果,我们对SQL查询的实际差异隐私提出了一组新要求。
2.为了满足这些要求,我们提出了弹性敏感度,即局部敏感性的近似为弹性敏感度[22,45],它支持一般的等值连接,仅使用查询本身和一组预先计算的数据库指标就可以有效地进行计算。我们证明弹性敏感度是局部敏感度的上限,因此可以使用任何基于局部敏感度的机制来强制执行差异性隐私。
3.我们设计和实现FLEX,这是一种基于弹性敏感性的SQL查询的端到端差异隐私系统。我们证明FLEX与任何现有数据库兼容,可以对大多数现实世界SQL查询强制实施差异性隐私,并产生可忽略的(0.03%)性能开销。
4.在此类的第一个实验评估中,我们使用FLEX评估差异隐私对数据集中9862个现实世界统计查询的影响。与以前对差异性隐私的经验评估相反,我们的实验集包含对真实数据执行的各种现实查询。我们证明FLEX对大多数这些查询引入了低错误。
【22】C. Dwork and J. Lei. Differential privacy and robust statistics. In Proceedings of the forty-fifirst annual ACM symposium on Theory of computing, pages 371–380. ACM, 2009.
【45】如上
我们设计和实现FLEX,这是一种基于弹性敏感性的SQL查询的端到端差异隐私系统。FLEX与任何现有数据库兼容,可以为大多数现实世界SQL查询强制实施差异隐私,性能开销0.03%。
2.实际差异隐私权要求
我们使用由Uber员工编写的SQL查询数据集。该数据集包含2013年3月至2016年8月之间对广泛的敏感数据(包括车手和驾驶员信息,旅行记录和客户支持数据)执行的810万次查询。
我们的实证研究的更多细节在本文的扩展版中提供[34]。
34是N. M. Johnson, J. P. Near, and D. X. Song. Towards practical differential privacy for SQL queries. CoRR, abs/1706.09479,2017.
当看一篇论文看不懂的时候,可以去找作者的主要参考文献或者作者的其他文章,肯定可以从其中找到一点蛛丝马迹的。
因此,一种实用的差异隐私机制将允许使用这些现有数据库中的任何一个,而不需要特定的数据库分发或定制的执行引擎来代替标准数据库。
研究表明,所有查询中有62.1%使用SQL Join 所有查询中有三分之一(34%)返回汇总统计信息。对于统计查询,Count是迄今为止最常见的聚合。
要求:我们总结了对实际SQL查询的实际差异隐私的要求:要求1:与现有数据库的兼容性。要求2:对等值连接的强大支持。
2.1已知有的差分隐私手段方法
1.Privacy Integrated Queries (PINQ)
这个方式是此论文中的方法 41 F. D. McSherry. Privacy integrated queries: an extensible platform for privacy-preserving data analysis. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of data, pages 19–30. ACM, 2009.
PINQ查询可以计算唯一连接键的数量,但不能计算连接结果的数量。此外,PINQ引入了标准SQL中不存在的新运算符,因此该方法与标准数据库不兼容。
2.wPINQ Weighted PINQ (wPINQ)
48方法 D. Proserpio, S. Goldberg, and F. McSherry. Calibrating data to sensitivity in private data analysis: A platform for differentially-private analysis of weighted datasets. PVLDB, 7(8):637–648, 2014.
扩展了PINQ以支持一般的等联接,并通过为数据库中的每一行分配权重,然后按比例缩小联接中各行的权重以确保整体敏感度为1来工作。但是与标准数据库不兼容。
3.Restricted sensitivity
限制敏感度[14]旨在通过使用辅助数据模型的属性来限制使用联接计数查询的全局敏感度。该方法要求全局限制每个连接键的频率(这对于一对一和一对多联接非常有效,因为联接“一”侧的唯一键具有全局范围。但是,它不能处理多对多联接,因为联接两侧的键的频率可能不受限制。无法与现有的数据库兼容。
4.DJoin
DJoin [43]是一种机制,用于对分布在多方之间的数据集进行差异化私有查询。DJoin仅支持一对一联接,因为它会将联接查询重写为关系交集。此外,该方法要求在查询执行期间使用特殊的加密功能,因此与现有数据库不兼容。
为了解决现有机制的局限性,我们提出了弹性敏感度。
3.弹性敏感度
3.1动机
弹性敏感度是一种用于计算查询局部敏感度上限的新颖方法。
基于局部敏感性的技术[22,45]通常比基于全局敏感性的方法更具实用性,因为它们考虑了实际的数据库。
先前的工作[45]描述了一种有效的方法,用于为有限的一组固定查询(例如,数据库中所有值的中位数)计算局部敏感度,但是这些技术不适用于通用查询或带有连接的查询。弹性敏感度是利用局部敏感度进行具有一般等联接的查询的第一种易于处理的方法。
我们方法的关键见解是使用有关真实数据库中联接键的频率的预先计算的指标,对查询中每个联接的影响进行建模。这种新颖的方法允许弹性敏感度计算局部敏感度的保守近似值,而无需与数据库进行任何其他交互。
我们证明了弹性敏感度是局部敏感度的上限,因此可以与任何基于局部敏感度的差异隐私机制一起使用
3.2背景
介绍了定义 1.差分隐私 2.全局敏感度 3.全局稳定性 4.局部敏感度 5.局部稳定性 6.局部敏感性的距离
3.3弹性灵敏度的定义
为了允许使用平滑函数,我们的定义描述了如何计算距真实数据库任意距离k的弹性敏感性。图1包含完整的定义,分为四个部分:(a)核心关系代数,(b)弹性灵敏度的定义,(c)距离k处的最大频率,以及(d)关系的祖先。接下来我们描述每个部分。这个定义没太看懂

Max frequency at distance k 距离k处的最大频率 最大频率度量用于限制连接的敏感性
Ancestors of a relation关系的祖先,自连接对敏感度的影响比不重叠关系的连接要大得多。
Join conditions 为简单起见,我们的符号仅指联接包含单个相等谓词的情况
3.4示例:计算三角形
这个例子完全看不懂,其中的敏感度的计算更加不懂。

3.5弹性敏感度是局部敏感度的上限
其中3.5节具体介绍了作者是如何证明弹性敏感度是局部敏感度的上界的,其证明过程我没有深究,只是去用他的结论即可。
3.6 Optimization for Public Tables
然后作者简单地介绍了如何对公共表优化的,添加了一个等值连接的公式。
3.7限制和扩展的讨论
3.7.1不支持的查询
弹性敏感性不支持非等值连接,并且添加对非等值连接的支持并不容易。
幸运的是,据我们研究超过四分之三的联接是等值联接。可以通过向数据库查询必要的数据相关范围来扩展弹性敏感性,以支持其他联接类型,但是对于每个原始查询,此修改将需要与数据库进行交互。
当由于查询结构而导致必需的最大频率指标不可用时,弹性敏感性也会失败。幸运的是,此条件在我们的数据集中占98.5%的联接,因此此限制在实践中几乎没有影响。
3.7.2支持其他聚合功能
1.值范围指标 2.求和and求平均数 3.最大值和最小值 4.四分位间距
四分位间距,它们对数据库的更改不太敏感。此策略在我们的设置中不可行,因为标准SQL不支持四分位数范围之类的功能
4. FLEX:SQL查询的实用差异特权

1.收集最大频率指标
弹性敏感度的定义需要数据库中的一组预先计算的指标mf,定义为每个连接键最频繁出现的属性的频率。使用SQL查询可以轻松获得mf的值。
体系结构非常适合于数据库更新的频率远低于数据库查询的环境。
弹性灵敏度分析。为了计算弹性敏感度,我们基于Presto解析器[9]构建了一个用于SQL查询的分析框架
【9】是Presto: Distributed SQL Query Engine for Big Data. https://prestodb.io/.
4.1正确性证明
FLEX实现了以下差分隐私机制,该机制是由Nissim等人定义的基于Laplace的平滑敏感度机制派生的。 [45,46]:这种机制利用弹性灵敏度作为局部灵敏度的上限来利用平滑灵敏度[45,46]。
45是K. Nissim, S. Raskhodnikova, and A. Smith. Smooth sensitivity and sampling in private data analysis. In Proceedings of the thirty-ninth annual ACM symposium on Theory of computing, pages 75–84. ACM, 2007.
4.2隐私预算和多重查询
稀疏向量技术[24]仅回答结果高于预定义阈值的查询。矩阵机制[38]和MWEM [30]算法使用基础机制的差分私有结果来构建真实数据库的近似值。然后,近似的数据库用于回答工作负载中的问题。丁等。 [19]使用类似的方法来发布差异私有数据立方体。
5.实验评估
我们通过以下实验评估我们的方法:•我们测量了实际查询中FLEX的性能开销和成功率(第5.1节)。 •我们研究了基于FLEX的差异性隐私在具有和不具有联接的实际查询中的效用(第5.2节)。 •我们评估隐私预算的效果吗?关于基于FLEX的差异隐私实用程序的信息(第5.3节)。 •我们测量第3.6节(第5.4节)中描述的公用表优化的效用影响。 •我们使用联接(第5.5节)在一组代表性计数查询上比较FLEX和wPINQ。
实验的环境是Java 8 on Mac OSX.
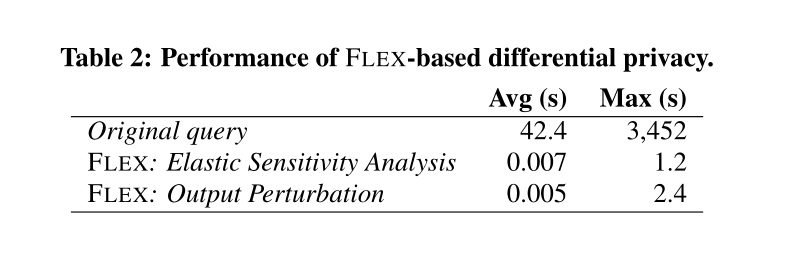
5.1 FLE的成功率和表现
FLEX总共成功计算出76%的查询的弹性敏感度,最多的错误组是由于查询不受支持(14.14%)。
5.2 FLEX在实际查询中的实用程序
对于小规模人群,我们希望我们的方法可以通过产生高错误来保护隐私;对于大量人口,我们希望我们的方法通过产生低误差来提供高实用性。
为了对查询进行计数,使用拉普拉斯噪声的基于局部灵敏度的机制有望表现出规模e可交换性。我们的结果提供了经验证明,即FLEX在计算局部敏感度的近似值时,无论有或没有联接,都保留此属性。
最后就是实验结果,与wPING对比。
5.3隐私预算的影响
高错误查询

5.5 与wPING工具相对比
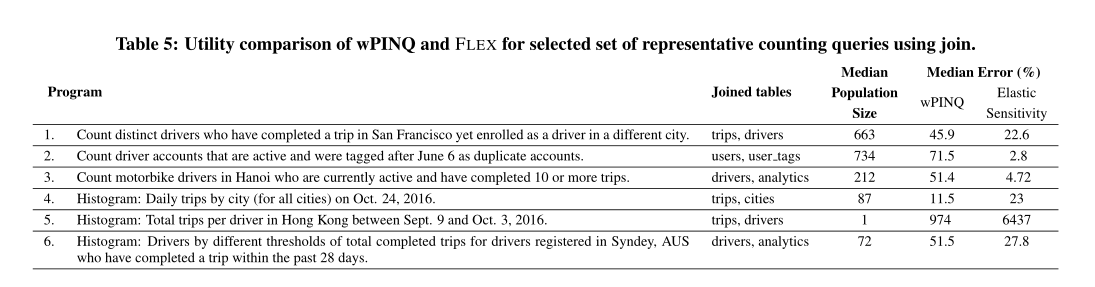
6.相关工作
差异隐私最初是由Dwork [20,21,23]提出的,而Dwork和Roth [25]的参考文献则很好地概述了差异隐私。这项工作大部分集中在发布特定算法结果的机制上。相反,我们的重点是支持通用等联接的SQL查询通用机制。我们在第2.1节中调查了支持加入的现有一般机制。 Lu等。 [39]提出了一种机制,用于生成差分私有综合数据,以使具有联接的查询在综合数据库和真实数据库上具有相似的性能特征,但不一定具有相似的答案。但是,Lu等,不要提出一种机制来回答具有差异性隐私的查询。因此,它不满足第2节中的两个要求。Airavat [49]强制执行任意MapReduce程序的差异隐私,但是要求分析人员限制程序可能输出的范围,并将输出值限制在该范围内这个范围。 Fuzz [28,29]对功能程序实施了不同的隐私保护,但不支持一对多或多方连接。提议测试发布[22](PTR)是一个利用局部敏感性的框架,该框架可用于任意实值函数。 PTR需要(但未定义)一种计算函数局部灵敏度的方法。我们在弹性敏感度方面的工作是相辅相成的,可以通过限制局部敏感度来启用PTR。样本和汇总[45,46]是适用于所有统计估计量的依赖数据的框架。它的工作方式是将数据库分为多个块,在每个块上运行查询,然后使用差分私有算法汇总结果。样本和聚合不支持连接,因为拆分数据库中断连接语义,也不支持不是统计估计量的查询,例如对查询进行计数。 GUPT [42]是一个实用的系统,它利用示例和汇总框架来为通用分析提供不同的隐私。指数机制[40]支持产生分类(而不是数字)数据的查询。它通过根据分析人员提供的评分功能从可能的输出中随机选择来工作。扩展FLEX以支持指数机制将需要指定评分功能,并需要一种方法来限制其敏感性。已经提出了许多用于执行特定图形分析任务的较不通用的机制[31、35、36、50]。这些任务通常涉及联接,但是用于处理它们的机制特定于任务,不适用于通用分析。例如,递归机制[16]在图分析的上下文中支持一般的等值连接,但仅限于单调查询,并且在最坏的情况下,数据库中参与者的数量按时间指数运行。 Kiferetal。[37]指出数据库约束(例如主键的唯一性)可能导致私有数据泄漏。这种约束在实践中很常见,并且引起了所有差异隐私方法的关注。 Kifer等。提出基于所涉及的特定约束来增加灵敏度,但是计算该灵敏度在计算上是困难的。开发一种易于处理的方法来解决常见约束(例如主键唯一性)是将来工作的有趣目标。
7.结论
本文迈出了迈向针对通用SQL查询的实际差异隐私的第一步。为了满足现实世界中SQL查询的要求,我们提出了弹性敏感性,这是第一种有效计算的支持联接的局部敏感性的近似方法。我们已经发布了一个用于计算SQL查询弹性敏感性的开源工具[4]。我们使用弹性敏感度来构建FLEX,这是一种用于对SQL查询强制实施差异隐私的系统。我们对各种各样的查询进行了FLEX评估,表明FLEX可以支持真实世界的查询,并且可以对大多数人口众多的查询提供高实用性。