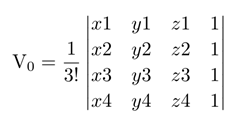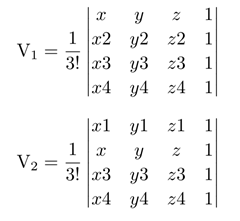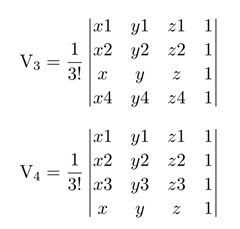点是否在 三角形,凸多边形, 凹多边形,四面体内 的判断

今天下午偶然瞄了一眼编程之美, 看到了一个问题,  4.4 点是否在多边形内.  为什么关注这个问题呢? 因为在今年给中科院保送研究生机试出题的时候,我也出了一道这样的题目.

看了编程之美的解答之后, 感觉作者没有把这个问题讲清楚, 所以来写这样一个东西.

<编程之美>的两种解答方案都很直观, 一种是 秦九韶海伦公式来做面积判断, 一种是 常用的判断点是否在三角形内.

为什么说 <编程之美> 没有讲清楚问题呢? 因为实质上这两种方法是统一的.

对于三角形的情况, 我们使用有向面积来判断,假设三角形三个点为(x1,y1),(x2,y2), (x3,y3), 需要判断的点为(x,y). 根据向量代数的公式, 已知3点坐标, 判断三角形有向面积为

有向面积的正负与行列式的排列顺序有关(交换行列式的任意两行, 行列式的正负发生变化)

简单的可以展开为 A0 = (x1y2 – x1y3 – x2y1 + x3y1 + x2y3 - x3y2)/2. 这个判断式子与 叉乘的判断的公式是一模一样的. 可以看出通过有向面积可以统一 <编程之美>中的两种方法, 面积与叉乘的方法在数学本质上是一致的.

 

在编程之美之后凹多边形的判断, 这个是图形学里面的一个经典问题, 从点(x,y)发出水平的射线, 判断与凹多边形的交点个数的奇偶性, 注意处理通过顶点的特殊情况.

 

如何判断一个点在四面体的内部呢? 使用有向体积的概念. 假设四面体的四个顶点的坐标为 (x1,y1,z1), (x2,y2,z2), (x3,y3,z3), (x4,y4,z4).  需要判断的点为(x,y,z). 那么原来四面体的有向体积 为

 

同理剩下的4个有向体积分别为

 

判断准则很简单, V0与V1V2V3V4都同向的时候, 则点位于四面体内, 否则位于四面体外.  当Vi = 0 的时候, 则此四面体退化了.