预100+70+40 实100+10+40
全国青少年信息学奥林匹克联赛模拟赛
mNOIP - 20171007
提高组 第一试

斐波那契(fibonacci)
【题目描述】
小 C 养了一些很可爱的兔子。
有一天,小 C 突然发现兔子们都是严格按照伟大的数学家斐波那契提出的模型来进行
繁衍: 一对兔子从出生后第二个月起, 每个月刚开始的时候都会产下一对小兔子。 我们假定,
在整个过程中兔子不会出现任何意外。
小 C 把兔子按出生顺序,把兔子们从 1 开始标号,并且小 C 的兔子都是 1 号兔子和 1
号兔子的后代。如果某两对兔子是同时出生的,那么小 C 会将父母标号更小的一对优先标
号。
如果我们把这种关系用图画下来,前六个月大概就是这样的:

其中,一个箭头 A → B 表示 A 是 B 的祖先,相同的颜色表示同一个月出生的兔子。
为了更细致地了解兔子们是如何繁衍的,小 C 找来了一些兔子,并且向你提出了 m 个
问题:她想知道关于每两对兔子 (a_i) 和 (b_i) ,他们的最近公共祖先是谁。你能帮帮小 C 吗?
一对兔子的祖先是这对兔子以及他们父母(如果有的话)的祖先,而最近公共祖先是指
两对兔子所共有的祖先中,离他们的距离之和最近的一对兔子。比如,5 和 7 的最近公共祖
先是 2,1 和 2 的最近公共祖先是 1,6 和 6 的最近公共祖先是 6。
【输入格式】
从文件(fibonacci.in)中读入数据。
第一行,包含一个正整数 (n)。
输入接下来 (n) 行,每行包含 2 个正整数,表示 (a_i) 和 (b_i) 。
【输出格式】
输出到文件 (fibonacci.out) 中。
输入一共 m行,每行一个正整数,依次表示你对问题的答案。
【样例 1 输入】
5
1 1
2 3
5 7
7 13
4 12
【样例 1 输出】
1
1
2
2
4
【样例 2】
见选手目录下的 (fibonacci/fibonacci2.in) 与 (fibonacci/fibonacci2.ans) 。
【数据范围与约定】
子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解
决一部分数据。
每个测试点的数据规模及特点如下表:

特殊性质 1:保证均为某一个月出生的兔子中标号最大的一对兔子。例如,对
于前六个月,标号最大的兔子分别是 (1, 2, 3, 5,8,13)
特殊性质 2:保证(|a_i-a_j|geq 1)。
f(n)=f(n-1)+f(n-2) 表示第n个月的兔子数,爱规则编号,第i月出生的第j只兔子序号为f(i-1)+j,他的爸爸显然是j
由此可以看出一个节点的父亲的编号就是它的编号减去比他小的的最大斐波那契数
#include<cstdio>
using namespace std;
#define LL long long
LL f[100];
void init() {
f[1]=1;f[2]=1;
for(int i=3;i<=61;i++) {
f[i]=f[i-1]+f[i-2];
/*if(f[i]>=1000000000000){
printf("%I64d %d
",f[i],i);
break;
}*/
}
}
LL lca(LL a,LL b) {
for(int i=61;a!=b;i--) {
if(a>f[i])a-=f[i];
if(b>f[i])b-=f[i];
//a-=f[i-1],b-=f[j-1];
}
return a;
}
int main () {
freopen("fibonacci.in","r",stdin);
freopen("fibonacci.out","w",stdout);
int m;
init();
scanf("%d",&m);
LL a,b;
while(m--) {
scanf("%I64d%I64d",&a,&b);
printf("%I64d
",lca(a,b));
}
return 0;
}
数颜色(color)
【题目描述】
小 C 的兔子不是雪白的,而是五彩缤纷的。每只兔子都有一种颜色,不同的兔子可能有
相同的颜色。 小 C 把她标号从 1 到 n 的 n 只兔子排成长长的一排, 来给他们喂胡萝卜吃。
排列完成后,第 (i) 只兔子的颜色是 (c_i) 。
俗话说得好,“萝卜青菜,各有所爱”。小 C 发现,不同颜色的兔子可能有对胡萝卜的
不同偏好。比如,银色的兔子最喜欢吃金色的胡萝卜,金色的兔子更喜欢吃胡萝卜叶子,而
绿色的兔子却喜欢吃酸一点的胡萝卜……为了满足兔子们的要求,小 C 十分苦恼。所以,为
了使得胡萝卜喂得更加准确,小 C 想知道在区间 ([l_j ,r_j ]) 里有多少只颜色为 (c_j) 的兔子。
不过,因为小 C 的兔子们都十分地活跃,它们不是很愿意待在一个固定的位置;与此同
时,小 C 也在根据她知道的信息来给兔子们调整位置。所以,有时编号为 (x_j) 和 (x_j+1) 的两
只兔子会交换位置。
小 C 被这一系列麻烦事给难住了。你能帮帮她吗?
【输入格式】
从文件 (color.in) 中读入数据。
1 行两个正整数 (n,m)。
第 2 行 n 个正整数,第 i 个数表示第 i 只兔子的颜色(c_i)。
输入接下来 ? 行,每行为以下两种中的一种:
“(1 l_j r_j c_j) ” :询问在区间 $[l_j ,r_j ] (里有多少只颜色为)c_j$的兔子;
“(2 x_j) ”: (x_j) 和 (x_i + 1) 两只兔子交换了位置。
【输出格式】
输出到文件 (color.out) 中。
对于每个 1 操作,输出一行一个正整数,表示你对于这个询问的答案。
【样例 1 输入】
6 5
1 2 3 2 3 3
1 1 3 2
1 4 6 3
2 3
1 1 3 2
1 4 6 3
【样例 1 输出】
1
2
2
3
【样例 1 说明】
前两个 1 操作和后两个 1 操作对应相同;在第三次的 2 操作后,3 号兔子和 4 号兔子
交换了位置,序列变为 1 2 2 3 3 3。
【样例 2】
见选手目录下的 (color/color2.in) 与 (color/color2.ans) 。
【数据范围】
子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解
决一部分测试数据。
对于所有测试点,有 (1 ≤ l_j < r_j ≤ n,1 ≤ x_j < n)。
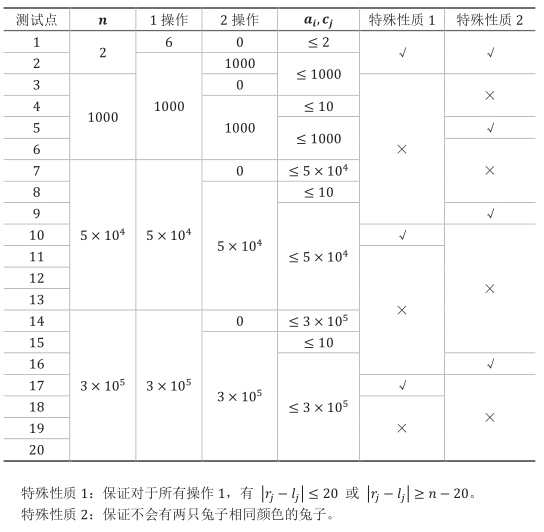
特殊性质 1:对于所有操作 1,有 (|r_j-l_j| ≤ 20) 或 (|r_j-l_j| ≥ n ? 20)。:
特殊性质 2:保证不会有两只兔子相同颜色的兔子。
开始写了个分块期望65
然后写炸了10分,听说可以分块写到100.,可是我不会,复杂度O(n(sqrt x))
你可以写主席树or动态开节点线段树or平衡树可以拿100
这里给出解法n:挨颜色,位置两个关键字排序,操作1只需要在数组上二分查找操作而不会改掉同种颜色兔子相对应的位子,只要swap一下就好复杂度O(nlogn)
解法N:
#include <bits/stdc++.h>
using namespace std;
#define MAXN 300005
int n, m;
int a[MAXN];
vector <int> b[MAXN];
int main() {
freopen("color.in", "r", stdin);
freopen("color.out", "w", stdout);
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", a + i);
b[a[i]].push_back(i);
}
for (int i = 1; i <= n; i++) sort(b[i].begin(), b[i].end());
for (int i = 1, x, l, r, c; i <= m; i++) {
scanf("%d", &x);
if (x == 1) {
scanf("%d%d%d", &l, &r, &c);
printf("%d
", (int)(upper_bound(b[c].begin(), b[c].end(), r) - lower_bound(b[c].begin(), b[c].end(), l)));
}
else {
scanf("%d", &x);
if (a[x] != a[x + 1]) {
(*lower_bound(b[a[x]].begin(), b[a[x]].end(), x))++;
(*lower_bound(b[a[x + 1]].begin(), b[a[x + 1]].end(), x + 1))--;
swap(a[x], a[x + 1]);
}
}
}
return 0;
}
分块
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn = 300007;
inline int read() {
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();return x*f;
}
int a[maxn],n,m;
int belong[maxn],block[519][300002],right[600],left[600];
inline void divide(int x) {
memset(right,0x3f,sizeof right);
right[0]=right[1]=0;
for(int i=1;i<=x;i++)
left[i]=right[i-1]+1,right[i]=i*x;
right[x]=n;
for(int i=1;i<=x;i++)
for(int j=left[i];j<=right[i];j++) {
belong[j]=i;
block[i][a[j]]++;
}
}
inline int query(int l,int r,int w) {
int b=belong[l];
int ans=0;int i;
for(i=l;i<=right[b]&&i<=r;++i)if(a[i]==w)ans++;
if(i-1==r) return ans;
for(i=b+1;right[i]<=r;++i) ans+=block[i][w];
for(i=right[i-1]+1;i<=r;++i)if(a[i]==w)ans++;
return ans;
}
inline void modify(int x,int y) {
int b1=belong[x],b2=belong[y];
if(b1!=b2)block[b1][a[x]]--,block[b1][a[y]]++,block[b2][a[y]]--,block[b2][a[x]]++;
swap(a[x],a[y]);
return;
}
int main() {
scanf("%d%d",&n,&m);
int num=sqrt(n);
num=n/num;
//printf("%d
",num);
for(int i=1;i<=n;++i)a[i]=read();
divide(num);
for(int aa,b,c,d,i=1;i<=m;i++) {
scanf("%d",&aa);
if(aa==1) {
scanf("%d%d%d",&b,&c,&d);
printf("%d
",query(b,c,d));
}
if(aa==2) {
scanf("%d",&b);
modify(b,b+1);
}
}
return 0;
}
分组(division)
【题目描述】
小 C 在了解了她所需要的信息之后,让兔子们调整到了恰当的位置。小 C 准备给兔子
们分成若干个小组来喂恰当的胡萝卜给兔子们吃。
此时, (n) 只兔子按一定顺序排成一排,第 i 只兔子的颜色是 (a_i) 。由于顺序已经是被
调整好了的,所以每个小组都应当是序列上连续的一段。
在分组前,小 C 发现了一个规律:有些兔子会两两发生矛盾。并且,两只兔子会发生矛
盾,当且仅当代表他们的颜色的数值之和为一个正整数的平方。比如,1 和 2 色兔子
不会发生矛盾, 因为 3 不是任何一个正整数的平方; 而 1 色兔子却会和 3 色兔子发生矛盾,
因为 (4 = 2^2) 。
小 C 认为,只要一个小组内的矛盾不要过大就行。因此,小 C 定义了一个小组的矛盾
值 ? , 表示在这个小组里, 至少需要将这个组再一次分成 (k) 个小团体; 每个小团体并不需
要是序列上连续的一段,但是需要使得每个小团体内任意两只兔子之间都不会发生矛盾。
小 C 要求,矛盾值最大的小组的矛盾值 (k) 不超过 (K) 就可以了。当然,这样的分组方
法可能会有很多个;为了使得分组变得更加和谐,小 C 想知道,在保证分组数量最少的情况
下,什么。你能帮帮她吗?
字典序最小的方案是指,按顺序排列分组的间隔位置,即所有存在兔子 i 和 i + 1 在
不同组的位置 i, 和其它所有相同分组组数相同的可行方案相比总有第一个不同的位置比其
它方案小的方案。
【输入格式】
从文件 (division.in) 中读入数据。
1 行两个正整数 n,k。
输入第 2 行 n 个正整数,第 (i)个数表示第 (i) 只兔子的颜色 (a_i) 。
【输出格式】
输出到文件 (division.out) 中。
第 1 行一个正整数 (m),为你至少需要将兔子分为多少个小组。
输出第 2 行 $m ? 1 $个从小到大的排列的正整数,第 i 个数 (s_i) 表示 (s_i) 和 (s_i + 1) 在
你的方案里被分到了两个小组。如果 m = 1,那么请输出一个空行。
【样例 1 输入】
5 2
1 3 15 10 6
【样例 1 输出】
2
1
【样例 1 解释】
如果将五只兔子全部分到同一个小组的话,那么((1, 3) (3, 6) (6, 10) (10, 15) (1, 15))均
不能分到同一个小团体;因为最多分成两个小团体,所以为了满足前 4 对限制,只能分为
({{1, 6, 15}, {3, 10}}),但此时不满足 ((1, 15)) ,所以不存在一种组数为 (1) 的方案满足全部限
制。
如果将五只兔子分为两个小组的话,一种字典序最小的可行的分组方案是 ({1}, {3, 15,)
$10, 6},此时第二组内的小团体数量不超过 2 的一种分法是 ({{3, 10}, {15, 6}})。
【样例 2】
见选手目录下的 (division/division2.in) 与 (division/division2.ans) 。
【数据范围】
子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解
决一部分数据。
每个测试点的数据规模及特点如下表:
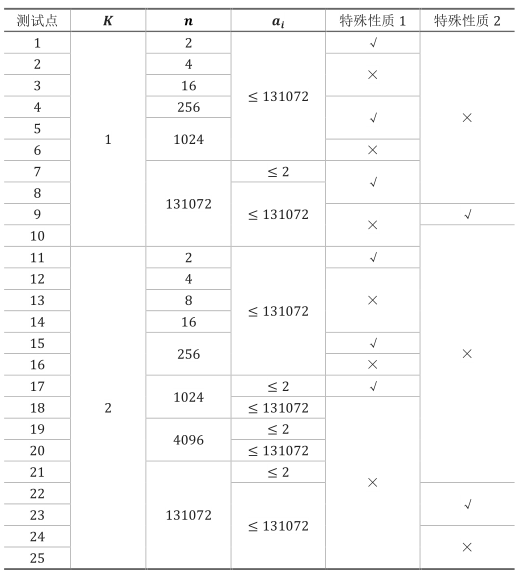
特殊性质 1:最优分组方案唯一。
特殊性质 2:保证不会有两只兔子相同颜色的兔子。
k=1的解法很好想,每个组不允许有矛盾,所以从后向前扩展,扫到的一定是字典序最小的最优解
k=2没写,写完k=1就弃疗了,结果检查了半个小时文件.......
k=2题解告诉了我N个部分分解提方案,不看了GG
上std
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
#define N 131073
int n, m = 0, K;
int a[N], b[N];
bool vis[N], dvis[N], issqr[N * 2];
int f[N * 2];
int getf(int x) {return f[x] > 0 ? (f[x] = getf(f[x])) : x;}
void merge(int u, int v) {
u = getf(u), v = getf(v);
if (u != v) {
if (f[u] > f[v]) swap(u, v);
f[u] += f[v];
f[v] = u;
}
}
bool check(int u, int v) {
int s1 = getf(u), s2 = getf(u + N);
int t1 = getf(v), t2 = getf(v + N);
if (s1 == t1) return 1;
if (s2 == t2) return 1;
merge(s1, t2); merge(s2, t1);
return 0;
}
void solve_1() {
for (int i = n, j = n; i;) {
for (bool flag = 1; j; j--) {
for (int k = 1; k * k - a[j] < N; k++) {
if (k * k - a[j] <= 0) continue;
if (vis[k * k - a[j]]) {flag = 0; break;}
}
if (!flag) break;
vis[a[j]] = 1;
}
if (!j) break;
b[++m] = j;
for ( ; i > j; i--) vis[a[i]] = 0;
}
}
void solve_2() {
memset(f, -1, sizeof f);
for (int i = 1; i * i < 2 * N; i++) issqr[i * i] = 1;
for (int i = n, j = n; i;) {
for (bool flag = 1; j; j--) {
if (vis[a[j]]) {
if (issqr[a[j] + a[j]]) {
if (dvis[a[j]]) break;
for (int k = 1; k * k - a[j] < N; k++) {
if (k * k - a[j] <= 0) continue;
if (vis[k * k - a[j]] && k * k != a[j] * 2) {
flag = 0; break;
}
}
if (!flag) break;
dvis[a[j]] = 1;
}
}
else {
for (int k = 1; k * k - a[j] < N; k++) {
if (k * k - a[j] <= 0) continue;
if (vis[k * k - a[j]]) {
if (check(k * k - a[j], a[j])) {flag = 0; break;}
}
}
if (!flag) break;
vis[a[j]] = 1;
}
}
if (!j) break;
b[++m] = j;
for ( ; i > j; i--) f[a[i]] = f[a[i] + N] = -1, vis[a[i]] = 0, dvis[a[i]] = 0;
}
}
int main() {
freopen("division.in", "r", stdin);
freopen("division.out", "w", stdout);
scanf("%d%d", &n, &K);
for (int i = 1; i <= n; i++) scanf("%d", a + i);
if (K == 1) solve_1();
else solve_2();
printf("%d
", m + 1);
for (int i = m; i; i--) printf("%d ", b[i]);
putchar('
');
return 0;
}