luoguP3768 简单的数学题

题目链接

luoguP3768 简单的数学题

题解

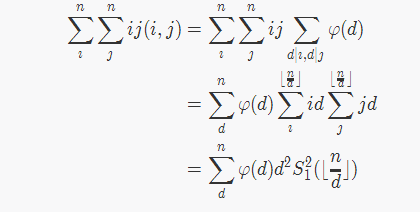
上面那个式子的最后一步，需要定理

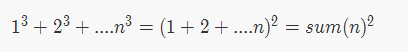
用数学归纳法证明
(S1=1^3=1^2)
(S2=1^3+2^3=9=3^2=(1+2)^2)
(S3=1^3+2^3+3^3=36=6^2=(1+2+3)^2)
(S4=1^3+2^3+3^3+4^3=100=10^2=(1+2+3+4)^2)
(S5=1^3+2^3+3^3+4^3+5^3=15^2=(1+2+3+4+5)^2)
假设当(n=k)时，有(Sk=1^3+2^3+...+k^3=(1+2+...+k)^2)
则当(n=(k+1))时，
(S(k+1)=Sk+ak=(1+2+...+k)^2+(k+1)^3)
(=[k(k+1)/2]^2+(k+1)^3)
(=(k+1)^2[k^2/4+k+1])
(=(k+1)^2[(k^2+4k+4)/4])
(=(k+1)^2(k+2)^2/4)
(=[(k+1)(k+2)/2]^2)
(=(1+2+...+k+1)^2)
对于前面那个杜教筛

代码

#include<map> 
#include<cstdio> 
#include<algorithm> 

inline int read() {
	int x = 0,f = 1; 
	char c = getchar(); 
	while(c < '0' || c > '9') { if(c == '-')f = -1; c = getchar(); } 
	while(c <= '9' && c >= '0') x = x * 10 + c - '0',c = getchar(); 
	return x * f; 
} 
#define LL long long 
const int maxn = 10000000;  
LL Max = maxn; 

std:: map<LL,LL>M; 
LL Inv6,Inv2,Phi[maxn + 7], phi[maxn + 7],mod; 
bool isprime[maxn + 7];  
int prime[maxn],cnt = 0; 
 
LL fstpow(LL a,LL b) { 
    LL ret = 1; 
    for(;b;b >>= 1,a = a * a % mod)  
        if(b & 1) ret = ret * a % mod; 
    return ret; 
}  

void getphi() { 
	phi[1] = 1; 
	for(int i = 2;i <= Max;++ i) { 
		if(!isprime[i]) prime[++ cnt] = i,phi[i] = (i - 1) % mod; 
		for(int j = 1;j <= cnt && i * prime[j] <= Max;++ j) { 
			isprime[i * prime[j]] = 1; 
			if(i % prime[j]) phi[i * prime[j]] = 1ll * phi[i] * phi[prime[j]] % mod; 
			else { 
				phi[i * prime[j]] = 1ll * phi[i] * prime[j] % mod; 
				break; 
			} 		
		} 
	} 
	for(int i = 1;i <= Max;++ i) Phi[i] = 1ll * phi[i] * i % mod * i % mod; 
	for(int i = 1;i <= Max;++ i) Phi[i] += Phi[i - 1] , Phi[i] %= mod; 
} 
//---------------------------------------------
LL S1(LL r) { r %= mod;return r * (r + 1) % mod * (r + r + 1) % mod * Inv6 % mod; } 
LL S2(LL r) { r %= mod;return r * (r + 1) % mod * Inv2 % mod; } 
LL S(LL n) {  
	if(n <= maxn) return Phi[n]; 
	if(M[n])      return M[n]; 
	LL he = S2(n) * S2(n) % mod , t; 
	for(LL i = 2,l;i <= n;i = l + 1) { 
		l = n / (n / i);  
		t = ((S1(l) - S1(i - 1)) % mod + mod) % mod; 
		he -= t * S(n / i) % mod,he %= mod; 
	} 
	return M[n] = (he + mod) % mod; 
} 
LL solve(LL n) { 
	LL res = 0;
	for(LL i = 1,l,t ;i <= n;i = l + 1) { 
	    l = n / (n / i),t = S2(n/i);
		res += ((S(l) - S(i - 1) + mod) % mod * (t * t % mod)) % mod; 
		res %= mod; 
	} 
	return (res + mod) % mod; 
} 

int main() { 
	LL n; 
	scanf("%lld%lld",&mod,&n);  
	Max = std::min(Max,n); 
	Inv2 = fstpow(2,mod - 2),Inv6 = fstpow(6,mod-2); 
	getphi(); 
	printf("%lld
",solve(n));  
	return 0; 
}