https://www.luogu.org/problem/show?pid=1471
一眼就能看出是线段树/树状数组题目了。
求平均不用说,线段树/树状数组维护区间和即可。
方差怎么求?先变换下方差公式:
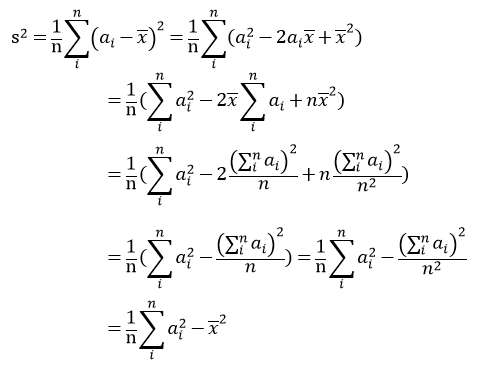
可以看到区间的方差可以由区间内每个数的和与每个数的平方的和得来,用一棵线段树维护这两个东西就好了,好像写不了标记永久化。
当然写两棵普通的线段树/树状数组分别维护这两个东西或者分块暴力也可以不过我写挂了。
区间加的时候如何维护平方的和:
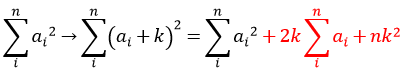
注意这里的![]() 是指没有加之前的和。
是指没有加之前的和。
#include <algorithm> #include <iostream> #define maxn 100005 using namespace std; namespace seg { struct node { int ln, rn, mn; long double sum[2], mark; } seg[maxn * 4]; void push_down(int p) { if (seg[p].mark && seg[p].ln != seg[p].rn) { seg[p * 2].mark += seg[p].mark; seg[p * 2].sum[1] += 2 * seg[p].mark * seg[p * 2].sum[0] + (seg[p * 2].rn - seg[p * 2].ln + 1) * seg[p].mark * seg[p].mark; seg[p * 2].sum[0] += (seg[p * 2].rn - seg[p * 2].ln + 1) * seg[p].mark; seg[p * 2 + 1].mark += seg[p].mark; seg[p * 2 + 1].sum[1] += 2 * seg[p].mark * seg[p * 2 + 1].sum[0] + (seg[p * 2 + 1].rn - seg[p * 2 + 1].ln + 1) * seg[p].mark * seg[p].mark; seg[p * 2 + 1].sum[0] += (seg[p * 2 + 1].rn - seg[p * 2 + 1].ln + 1) * seg[p].mark; seg[p].mark = 0; } } void init(int l, int r, int p) { seg[p].ln = l; seg[p].rn = r; seg[p].mn = (l + r) / 2; seg[p].mark = 0; if (l != r) { init(l, seg[p].mn, p * 2); init(seg[p].mn + 1, r, p * 2 + 1); seg[p].sum[0] = seg[p * 2].sum[0] + seg[p * 2 + 1].sum[0]; seg[p].sum[1] = seg[p * 2].sum[1] + seg[p * 2 + 1].sum[1]; } else { cin >> seg[p].sum[0]; seg[p].sum[1] = seg[p].sum[0] * seg[p].sum[0]; } } void increase(int l, int r, long double val, int p) { if (seg[p].ln == l && seg[p].rn == r) { seg[p].mark += val; seg[p].sum[1] += 2 * val * seg[p].sum[0] + (r - l + 1) * val * val; seg[p].sum[0] += (r - l + 1) * val; } else { push_down(p); if (l <= seg[p].mn) increase(l, min(r, seg[p].mn), val, p * 2); if (seg[p].mn + 1 <= r) increase(max(l, seg[p].mn + 1), r, val, p * 2 + 1); seg[p].sum[0] = seg[p * 2].sum[0] + seg[p * 2 + 1].sum[0]; seg[p].sum[1] = seg[p * 2].sum[1] + seg[p * 2 + 1].sum[1]; } } long double sum(int l, int r, int p, int emm) { if (seg[p].ln == l && seg[p].rn == r) { return seg[p].sum[emm]; } else { push_down(p); long double ans = 0; if (l <= seg[p].mn) ans += sum(l, min(r, seg[p].mn), p * 2, emm); if (seg[p].mn + 1 <= r) ans += sum(max(l, seg[p].mn + 1), r, p * 2 + 1, emm); return ans; } } } int n, m; int main() { ios::sync_with_stdio(false); cout.precision(4); // 控制精度用 cin >> n >> m; seg::init(1, n, 1); int opt, l, r; long double k; long double aver, aver2; long double sum, sum2; while (m--) { cin >> opt >> l >> r; if (opt == 1) { cin >> k; seg::increase(l, r, k, 1); } else { sum = seg::sum(l, r, 1, 0); sum2 = seg::sum(l, r, 1, 1); aver = sum / (long double)(r - l + 1); aver2 = sum2 / (long double)(r - l + 1); if (opt == 2) cout << fixed << aver << endl; else cout << fixed << aver2 - aver * aver << endl; } } return 0; }