机器学习作业---偏差和方差（线性回归）

机器学习作业---偏差和方差（线性回归）错误反例，但是理清了代码思路，很重要

一：加载数据，显示数据

（一）数据可视化

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio
import scipy.optimize as opt


data = sio.loadmat("ex5data1.mat")

X = data['X']
y = data['y'].flatten()
Xval = data['Xval']
yval = data['yval'].flatten()
Xtest = data['Xtest']
ytest = data['ytest'].flatten()

m = y.size

plt.figure()
plt.scatter(X,y,c='b',marker='o')
plt.xlabel("Change in water level (x)")
plt.ylabel("Water folowing out of the dam (y)")
plt.show()

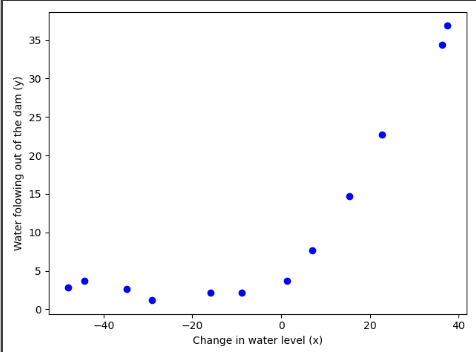
（二）数据显示

直接从文件中读取的数据X:

[[-15.93675813]
 [-29.15297922]
 [ 36.18954863]
 [ 37.49218733]
 [-48.05882945]
 [ -8.94145794]
 [ 15.30779289]
 [-34.70626581]
 [  1.38915437]
 [-44.38375985]
 [  7.01350208]
 [ 22.76274892]]

直接从文件中读取的数据y:

[[ 2.13431051]
 [ 1.17325668]
 [34.35910918]
 [36.83795516]
 [ 2.80896507]
 [ 2.12107248]
 [14.71026831]
 [ 2.61418439]
 [ 3.74017167]
 [ 3.73169131]
 [ 7.62765885]
 [22.7524283 ]]

可以知道都是二维数组类型。

将y展开为一维数组后：

[ 2.13431051  1.17325668 34.35910918 36.83795516  2.80896507  2.12107248
 14.71026831  2.61418439  3.74017167  3.73169131  7.62765885 22.7524283 ]

二：代价函数实现

（一）代码实现

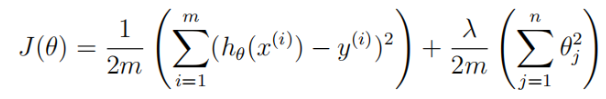
def reg_cost(theta,X,y,lamda):
    # 我们在这里将输入的X前面加上一列1，用来匹配截距θ_0
    m = y.size
    X = np.c_[np.ones(m),X]
    reg_theta = theta[1:]
    #返回正则化代价函数
    hythesis = np.dot(X,theta)-y
    return np.sum(np.power(hythesis,2))/(2*m) + np.sum(np.power(reg_theta,2))*lamda/(2*m)

（二）测试结果

theta = np.ones(X.shape[1]+1)
cost = reg_cost(theta,X,y,1)
print(cost)

三：实现梯度求解参数 

（一）代码实现

def reg_gradient(theta,X,y,lamda=1):
    m = y.size
    X = np.c_[np.ones(m),X]
    reg_theta = theta[1:]
    hythesis = np.dot(X,theta)-y
    #可以看到和代价函数还是有好多重复，所以后面推荐一个函数实现
    theta_grad = np.dot(hythesis,X)/m
    theta_grad[1:]+=theta[1:]*lamda/m

    return theta_grad

（二）结果测试

返回的是一维数组来表示参数向量 

四：使用高级优化算法求解参数向量、拟合数据

（一）使用高级优化算法求解参数

res = opt.minimize(fun=reg_cost,x0=theta,args=(X,y,1),method="TNC",jac=reg_gradient)
print(res)

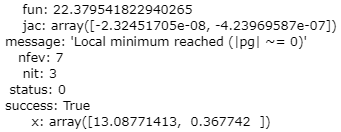
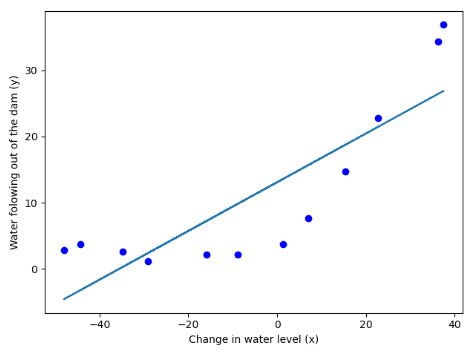
（二）可视化拟合程度

res = opt.minimize(fun=reg_cost,x0=theta,args=(X,y,1),method="TNC",jac=reg_gradient)
theta_new = res.x

plt.figure()
plt.scatter(X,y,c='b',marker='o')
plt.plot(X,theta_new[1]*X+theta_new[0])
plt.xlabel("Change in water level (x)")
plt.ylabel("Water folowing out of the dam (y)")
plt.show()

五： 绘制学习曲线（重点）

重点：

1.使用训练集的子集来拟合数据--获取本次循环最优参数

2.在计算训练代价（误差）和交叉验证代价（误差）时，不需要使用正则化

3.使用相同的验证集自己来计算训练代价

（一）实现获取训练误差、验证误差

def learning_curve(X,y,Xval,yval,lamda):
    m = y.size

    error_train = np.zeros(m)
    error_val = np.zeros(m)

    for i in range(m):
        # 获取新的临时训练样本集---重点事项1
        X_temp = X[:i+1]
        y_temp = y[:i+1]

        theta = np.ones(X.shape[1]+1)
        #获取当前训练集样本下的最优参数θ向量
        res = opt.minimize(fun=reg_cost,x0=theta,args=(X_temp,y_temp,lamda),method="TNC",jac=reg_gradient)
        theta_new = res.x

        # 根据上面获得的最优参数向量，我们获取训练集误差---注意：训练集误差的数据集来自于我们新的训练集
        error_train[i] = reg_cost(theta_new,X_temp,y_temp,lamda)
        # 验证集误差，数据集来自于全部验证集
        # 每次都是将所有验证集进行计算误差----重点事项3
        error_val[i] = reg_cost(theta_new,Xval,yval,lamda)

    return error_train,error_val

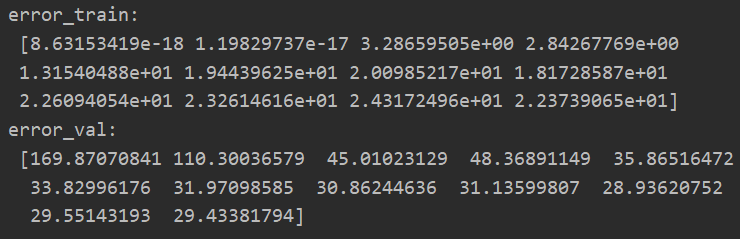
#绘制学习曲线
##设置lamda为0，不进行正则化处理---重点事项2
error_train,error_val = learning_curve(X,y,Xval,yval,lamda=0)
print("error_train:
",error_train)
print("error_val:
",error_val)

（二）绘制学习曲线图像  

plt.figure()
plt.plot(np.arange(X.shape[0]),error_train,np.arange(X.shape[0]),error_val)
plt.title("Learning Curve for linear regression")
plt.xlabel("Number of Training Examples")
plt.ylabel("Error")
plt.legend(['Train','Cross Validation'])
plt.show()

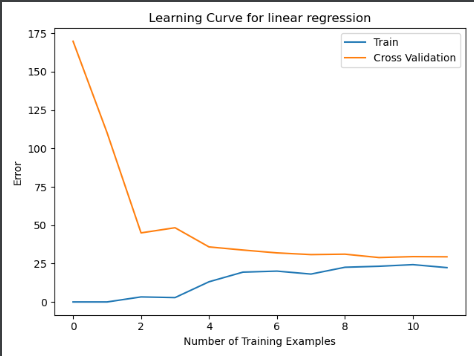
（三）学习曲线得出结论---高偏差（欠拟合）

绘制非正则化学习曲线图，随着训练样本数量的增加，训练误差和交叉验证逐渐接近，但误差较大，高偏差、欠拟合---增大训练样本无用（高偏差）

六：改进机器学习系统性能的方法

当我们运用训练好了的模型来预测未知数据的时候发现有较大的误差，我们下一步可以做什么？

获得更多的训练实例——通常是有效的，但代价较大，下面的方法也可能有效，可考虑先采用下面的几种方法：

1. 获得更多的训练实例——解决高方差

2. 尝试减少特征的数量——解决高方差

3. 尝试获得更多的特征——解决高偏差

4. 尝试增加多项式特征——解决高偏差

5. 尝试减少正则化程度λ——解决高偏差

6. 尝试增加正则化程度λ——解决高方差

我们不应该随机选择上面的某种方法来改进我们的算法，而是运用一些机器学习诊断法来帮助我们知道上面哪些方法对我们的算法是有效的。

（一）获取更多训练数据---解决高方差（后面再补充，可能有问题）

见：https://www.cnblogs.com/ssyfj/p/12872699.html（六：学习曲线）

前提是：

1.我们已经使用全部训练集得出了一个模型，该模型可能存在过拟合或者欠拟合问题。下面将说明训练集数据增大后对这个模型的影响。

例如：对于下面数据，我们提出下面线性模型：

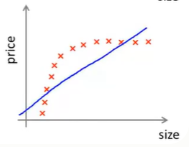
 则无论我们如何改变参数θ，依旧存在欠拟合情况。

2.同时为了我们方便判断这个模型的到底是过拟合还是欠拟合，我们通过绘制学习曲线来进行判断。

1.增大训练集数据，对高偏差无用---（已有模型，该模型欠拟合）

高偏差（欠拟合）：预测值与实际值之间的偏离程度

只是一条直线来减小拟合是不可能对这组数据进行很好得拟合。所以当我们给出交叉验证集误差随着m得增大得图像时，会发现，误差会随着m增大逐渐减小，但是会存在一个下界。

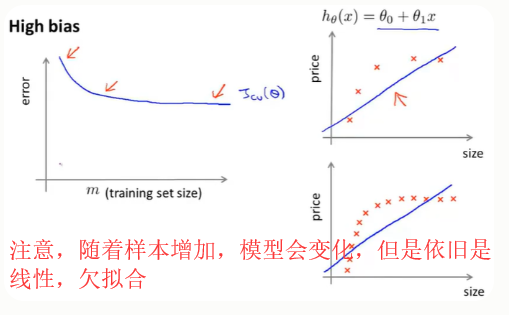
同样训练误差一开始也是很小的，而在高偏差的情况下，你会发现训练集误差会逐渐增大，最后接近交叉验证误差：

2.增大数据集数据，对高方差有用 ---（已有模型，该模型过拟合）

高方差（过拟合）：预测值变化波动情况

训练误差---当训练样本越多的时候，就越难把训练集数据拟合得更好。但总的来说训练集误差还是很小得

其学习曲线如下：

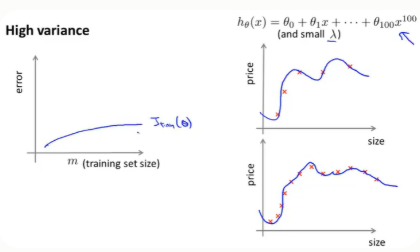
交叉验证误差---过拟合下（泛化能力很差），验证误差将会一直很大，尽管随着样本增大，但是总的来说还是很大。

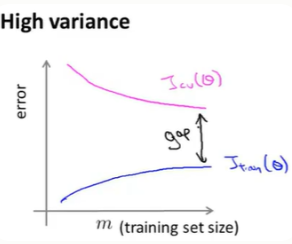
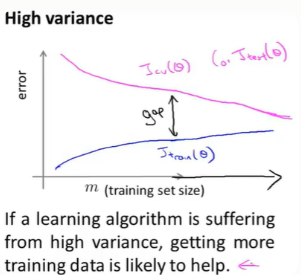
其特点是：在训练误差和交叉验证误差之间有一段很大的差距。

当我们增大样本数量时，训练误差会增大，而验证误差会减少。所以高方差下，增大样本数量还是有用的。 

（二）多项式特征

对于训练集，当d较小时，模型拟合程度更低，误差较大；随着d的增长，拟合程度提高，误差减小。

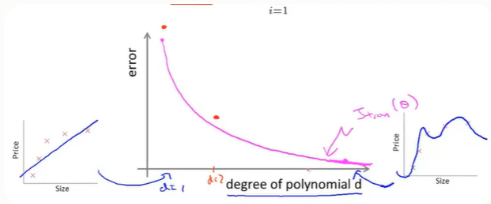
对于交叉验证集，当d较小时，模型拟合程度低，误差较大；但是随着d的增长，误差呈现先减小后增大的趋势，转折点是我们的模型开始过拟合训练数据集的时候。

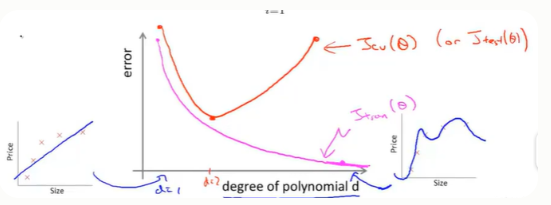
 训练集误差和交叉验证集误差近似时：偏差/欠拟合---多项式次数d太小，我们应该适当增大

 交叉验证集误差远大于训练集误差时：方差/过拟合---多项式次数d太大，我们应该适当减小

（三）正则化程度入---线性回归举例

1.当我们设置入较大时，比如入=1000，这时θ_1,...,θ_m都将受到很大的惩罚。所以θ_1,...,θ_m几乎都等于0.这时H_θ(x)≈θ_0

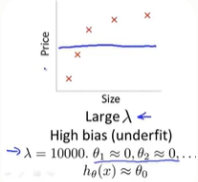
因此这个假设处于高偏差，对数据集严重欠拟合。

2.与之对应的另一种情况是，如果我们的lambda值很小，比如说lambda的值等于0的时候，在这种情况下，如果我们要拟合一个高阶多项式的话，那么此时我们通常会处于过拟合的情况。

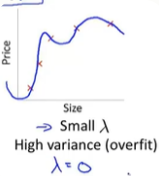
3.只有当我们取一个中间大小的，既不大也不小的lambda值时，我们才会得到一组合理的，对数据刚好拟合的theta参数值

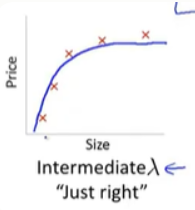
学习曲线如下：

当入较小时，训练集误差较小（过拟合）而交叉验证集误差较大--高方差

随着入的增加，训练集误差不断增加（欠拟合），而交叉验证集误差则是先减小后增加---高偏差

七：增加多项式特征解决欠拟合问题 

从我们在五中学习曲线中，可以看出，使用线性模型模型存在欠拟合（高偏差）状态，所以这里我们为了解决欠拟合问题，应该尝试增加多项式特征。

（一） 增加特征，扩展特征（从1到10阶）

def poly_feature(X,p):  #传入训练集数据和多项式次数---因为原来只有一个x_1特征项，所以这里我们增加特征，是x_1^n,没有中间项
    X_poly = np.zeros((X.shape[0],p))   #由原来m行，1列，变为m行p列
    p = np.arange(1,p+1)
    X_poly = X**p   #获取多项式特征
    return X_poly

p = 8　　#这里用8阶来测试我们的函数

X_poly = poly_feature(X,p)
print(X_poly.shape)
print(X_poly)

补充：两个向量之间进行平方运算

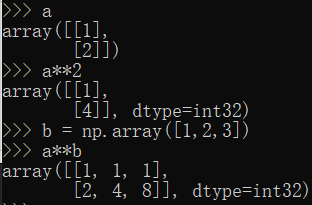
a**b,b会对a进行列扩展。

（二）获取扩展多项式后训练集的均值和方差

在进行归一化处理之前，我们需要获取均值和方差（和我们五中，获取theta一样），是从训练集中获取数据信息，然后运用到后面训练集、验证集、测试集中进行归一化处理。并且在绘制拟合图形和学习曲线时，都会受到我们从训练集中获取的均值和方差影响。

def get_mean_std(X):
    fea_mean = np.mean(X,0) #对特征进行均值求解（按列）
    sigma = np.std(X,0,ddof=1)  #ddof=0求解总体标准差，ddof=1求解样本标准差
    return fea_mean,sigma

p = 6　　#这里用6阶来进行测试
lmd = 0

X_poly = poly_feature(X,p)

mean,sigma = get_mean_std(X_poly)
print("mu:
",mean)
print("sigma:
",sigma)

X_norm = feature_normalize(X_poly,mean,sigma)

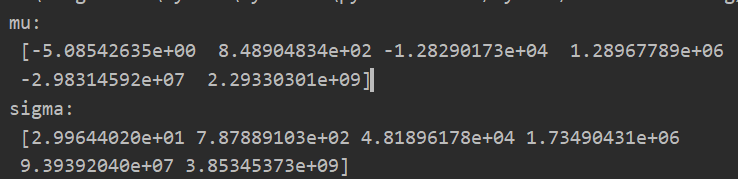
（三）归一化数据 （6阶来测试）

对于我们进行扩展后的多项式，各个特征中的数据大小差异可能过大，我们要进行归一化处理，防止某一个特征影响太大，从而影响其他特征的作用。这里我们使用标准差标准化。

标准差标准化： x =(x - u)/σ u是均值 σ是标准差

def feature_normalize(X,mean,sigma):
    X_norm = (X-mean)/sigma #对每一行都减去这个均值
    return X_norm

（四）对训练数据、验证样本、测试样本进行多项式处理、归一化处理（6阶测试）

X_poly = poly_feature(X,p)

mean,sigma = get_mean_std(X_poly)
print("mu:
",mean)
print("sigma:
",sigma)

X_norm = feature_normalize(X_poly,mean,sigma)

X_val_poly = poly_feature(Xval,p)
X_val_norm = feature_normalize(X_val_poly,mean,sigma)

X_test_poly = poly_feature(Xtest,p)
X_test_norm = feature_normalize(X_test_poly,mean,sigma)

print("X_norm:
",X_norm[:1])
print("X_val_norm:
",X_val_norm[:1])

（五）高级优化算法获取多项式参数向量

theta = np.ones(p+1)　　#p=6,lmd=0

#绘制原始数据集和我们新的多项式模型---查看拟合状态
res = opt.minimize(fun=reg_cost,x0=theta,args=(X_norm,y,lmd),method="TNC",jac=reg_gradient)
theta_new = res.x
print(theta_new)

（六）获取训练误差和验证误差

def poly_learning_curve(X,y,Xval,yval,p_f,lamda):
    error_train = np.zeros(p_f)
    error_val = np.zeros(p_f)

    lmd = 0

    for p in range(1,p_f+1):
        # 获取新的临时训练样本集---重点事项1
        X_poly = poly_feature(X, p)
        mean, sigma = get_mean_std(X_poly)
        X_norm = feature_normalize(X_poly, mean, sigma)

        X_val_poly = poly_feature(Xval, p)
        X_val_norm = feature_normalize(X_val_poly, mean, sigma)

        theta = np.ones(p + 1)

        # 绘制原始数据集和我们新的多项式模型---查看拟合状态
        res = opt.minimize(fun=reg_cost, x0=theta, args=(X_norm, y, lmd), method="TNC", jac=reg_gradient)
        theta_new = res.x

        # 根据上面获得的最优参数向量，我们获取训练集误差---注意：训练集误差的数据集来自于我们新的训练集
        error_train[p-1] = reg_cost(theta_new,X_norm,y,lamda)
        # 验证集误差，数据集来自于全部验证集
        # 每次都是将所有验证集进行计算误差----重点事项3
        error_val[p-1] = reg_cost(theta_new,X_val_norm,yval,lamda)

    print("error_train:
",error_train)
    print("error_val:
",error_val)
    return error_train,error_val

data = sio.loadmat("ex5data1.mat")

X = data['X']
y = data['y'].flatten()
Xval = data['Xval']
yval = data['yval'].flatten()
Xtest = data['Xtest']
ytest = data['ytest'].flatten()

m = y.size
theta = np.ones(X.shape[1]+1)

lmd = 0
p = 10

#绘制学习曲线
##设置lamda为0，不进行正则化处理---重点事项2
error_train,error_val = poly_learning_curve(X,y,Xval,yval,p,lmd)

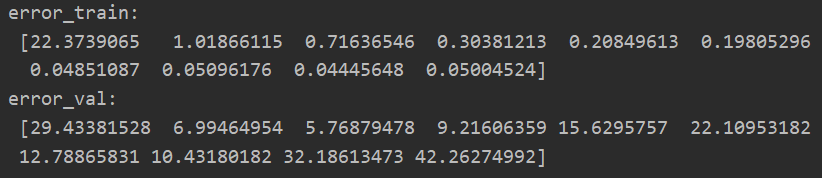
（七）绘制学习曲线---用于判断求取合适的多项式项数

#绘制学习曲线
##设置lamda为0，不进行正则化处理---重点事项2
error_train,error_val = poly_learning_curve(X,y,Xval,yval,p,lmd)

plt.figure()
plt.plot(np.arange(1,p+1),error_train,np.arange(1,p+1),error_val)
plt.title("Learning Curve for linear regression")
plt.xlabel("Number of Poly Feature")
plt.ylabel("Error")
plt.legend(['Train','Cross Validation'])
plt.show()

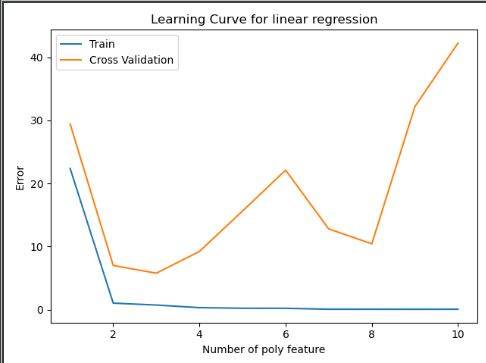
由六（二）可以知道，我们选取项数为3时，可以很好的拟合数据集！！！

（八）绘制拟合图形

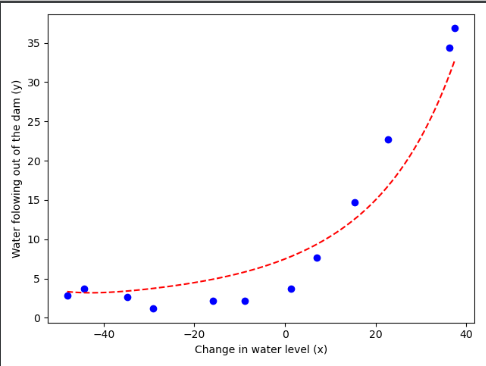
#产生一系列新的x坐标值，一会用于绘制拟合曲线
p = 3
theta = np.ones(p + 1)

X_poly = poly_feature(X, p)
mean, sigma = get_mean_std(X_poly)
X_norm = feature_normalize(X_poly, mean, sigma)

# 绘制原始数据集和我们新的多项式模型---查看拟合状态
res = opt.minimize(fun=reg_cost, x0=theta, args=(X_norm, y, lmd), method="TNC", jac=reg_gradient)
theta_new = res.x

# print(np.min(X),np.max(X))  #-48.058829452570066 37.49218733199513 所以我们取-60到60
x_plot = np.linspace(np.min(X),np.max(X),100).reshape(100,1) #转为列向量
x_plot_poly = poly_feature(x_plot,p)
x_plot_norm = feature_normalize(x_plot_poly,mean,sigma)

#获取y值
#print(x_plot_norm.shape,theta_new.shape)    #(100, 8) (9,)
#先向我们坐标序列加一列
x_plot_norm = np.c_[np.ones(100),x_plot_norm]   #(100, 9)
y_plot = np.dot(x_plot_norm,theta_new)  #(100,)

plt.figure()
plt.scatter(X,y,c='b',marker='o')   #绘制原始数据集
#开始绘制拟合曲线
plt.plot(x_plot,y_plot,'r--')
plt.xlabel("Change in water level (x)")
plt.ylabel("Water folowing out of the dam (y)")
plt.show()

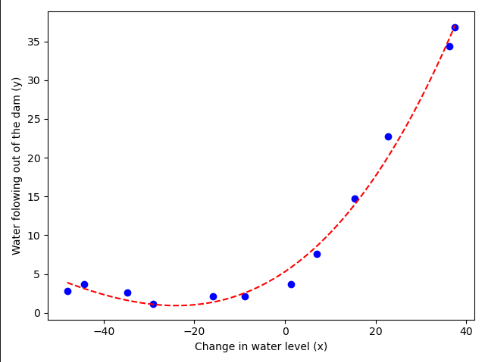
八：讨论正则化程度入对数据的影响

由于我们上面使用了多项式解决了欠拟合问题，这里我们使用正则化参数入来解决一个过拟合问题！！！

从七中，我们可以知道，当我们项数小于3时，趋于欠拟合（高偏差），当我们选取的项数大于3时，趋于过拟合（高方差）。

所以我们这里选取多项式特征为6，以此为基础来解决过拟合问题！！！

（一）设置多项式特征为6，入=0，进行过拟合测试，绘制拟合图形

#产生一系列新的x坐标值，一会用于绘制拟合曲线
p = 6
lmd = 0

theta = np.ones(p + 1)

X_poly = poly_feature(X, p)
mean, sigma = get_mean_std(X_poly)
X_norm = feature_normalize(X_poly, mean, sigma)

# 绘制原始数据集和我们新的多项式模型---查看拟合状态
res = opt.minimize(fun=reg_cost, x0=theta, args=(X_norm, y, lmd), method="TNC", jac=reg_gradient)
theta_new = res.x

# print(np.min(X),np.max(X))  #-48.058829452570066 37.49218733199513 所以我们取-60到60
x_plot = np.linspace(np.min(X),np.max(X),100).reshape(100,1) #转为列向量
x_plot_poly = poly_feature(x_plot,p)
x_plot_norm = feature_normalize(x_plot_poly,mean,sigma)

#获取y值
#print(x_plot_norm.shape,theta_new.shape)    #(100, 8) (9,)
#先向我们坐标序列加一列
x_plot_norm = np.c_[np.ones(100),x_plot_norm]   #(100, 9)
y_plot = np.dot(x_plot_norm,theta_new)  #(100,)

plt.figure()
plt.scatter(X,y,c='b',marker='o')   #绘制原始数据集
#开始绘制拟合曲线
plt.plot(x_plot,y_plot,'r--')
plt.xlabel("Change in water level (x)")
plt.ylabel("Water folowing out of the dam (y)")
plt.show()

与我们上面获得的，多项式特征为3比较，发现在两端有明显过拟合现象。所以下面我们通过修改正则化程度入来进行改善！！！

（二） 获取训练误差和验证误差

def reg_learning_curve(X,y,Xval,yval,lmds):
    error_train = np.zeros(len(lmds))
    error_val = np.zeros(len(lmds))

    for i in range(len(lmds)):
        theta = np.ones(X.shape[1]+1)
        lmd = lmds[i]
        # 绘制原始数据集和我们新的多项式模型---查看拟合状态
        res = opt.minimize(fun=reg_cost, x0=theta, args=(X_norm, y, lmd), method="TNC", jac=reg_gradient)
        theta_new = res.x

        # 根据上面获得的最优参数向量，我们获取训练集误差---注意：训练集误差的数据集来自于我们新的训练集
        error_train[i] = reg_cost(theta_new,X,y,0)
        # 验证集误差，数据集来自于全部验证集
        # 每次都是将所有验证集进行计算误差----重点事项3
        error_val[i] = reg_cost(theta_new,Xval,yval,0)
    return error_train,error_val

重点注意：五中提及的，对于我们后面的训练集、验证集求解误差时，不需要进行正则化，所以我们需要将其入设置为0！！！

#绘制学习曲线
p = 6
lmds = [0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]

X_poly = poly_feature(X, p)
mean, sigma = get_mean_std(X_poly)
X_norm = feature_normalize(X_poly, mean, sigma)

X_val_poly = poly_feature(Xval, p)
X_val_norm = feature_normalize(X_val_poly, mean, sigma)

# lam_error(X_norm,y,X_val_norm,yval)

error_train,error_val = reg_learning_curve(X_norm,y,X_val_norm,yval,lmds)

（三）绘制学习曲线---用于判断求取合适的正则化程度入值

plt.figure()
plt.plot(lmds,error_train,lmds,error_val)
plt.title("Learning Curve for linear regression")
plt.xlabel("Lamda")
plt.ylabel("Error")
plt.legend(['Train','Cross Validation'])
plt.show()

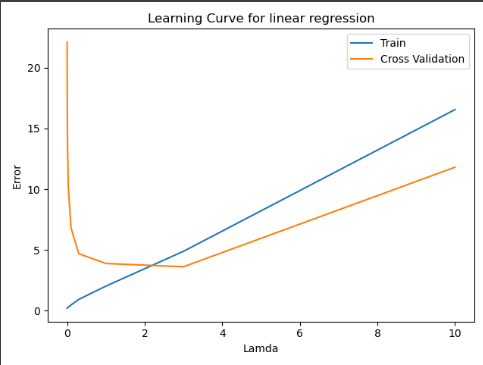
由六（三）可以知道，当我们选择正则化程度入值为3时，可以很好的防止过拟合！！！

（四）绘制拟合图形

#产生一系列新的x坐标值，一会用于绘制拟合曲线
p = 6
lmd = 3

theta = np.ones(p + 1)

X_poly = poly_feature(X, p)
mean, sigma = get_mean_std(X_poly)
X_norm = feature_normalize(X_poly, mean, sigma)

# 绘制原始数据集和我们新的多项式模型---查看拟合状态
res = opt.minimize(fun=reg_cost, x0=theta, args=(X_norm, y, lmd), method="TNC", jac=reg_gradient)
theta_new = res.x

# print(np.min(X),np.max(X))  #-48.058829452570066 37.49218733199513 所以我们取-60到60
x_plot = np.linspace(np.min(X),np.max(X),100).reshape(100,1) #转为列向量
x_plot_poly = poly_feature(x_plot,p)
x_plot_norm = feature_normalize(x_plot_poly,mean,sigma)

#获取y值
#print(x_plot_norm.shape,theta_new.shape)    #(100, 8) (9,)
#先向我们坐标序列加一列
x_plot_norm = np.c_[np.ones(100),x_plot_norm]   #(100, 9)
y_plot = np.dot(x_plot_norm,theta_new)  #(100,)

plt.figure()
plt.scatter(X,y,c='b',marker='o')   #绘制原始数据集
#开始绘制拟合曲线
plt.plot(x_plot,y_plot,'r--')
plt.xlabel("Change in water level (x)")
plt.ylabel("Water folowing out of the dam (y)")
plt.show()