读者前置要求:概率论。
在这一片文章中,我要讲的主要有两个核心问题:
(1)概率分布的表示方法。最基本的方法(naive)和利用了变量间独立关系的方法之前的差别是什么。
(2)为什么我们会引入概率图论模型,它的涵义是什么。
一、Parameterization of Distribution
我们大家都知道要充分描述一个概率分布只要列举出(假设的设计的随机变量是离散的)每一种事件发生的概率就行了。然而,其实还有另外的表示方法。这一部分的内容是在讲我们为什么要寻找另外的表示方法。
怎么表达 distribution
1、一个navie distribution是列出每种可能出现的结果,并给出他们的概率
2、如果存在独行性的化,我们可以另外的表示法。考虑N个不同硬币(biased)的投掷结果。
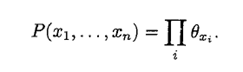
要表示这种概率分布,需要的参数仅仅是n.而之前,采用navie的方法,也就是我们对这个N个变量间的关系一无所知,则要表示好这个必须有2^N - 1 这么多的参数。
这里的其实在讲的是这么一件事情。
一个distribution其实一个函数。要定义出这个distribution有两种方法。
1、列举法。如果我们对其中变量间的关系毫无所知的时候,我们没有办法只能采用种办法。那么为了表达这样一组数值关系,我们要用的的独立参数(independent parameter)的个数是2^n -1.
2、其他的表示法。如果我们知道,变量间的独立关系。如果投硬币都是互相独立的。那么为了表达出这个函数/概率分布,我们所需要的独立参数仅仅是N。
可以预见的得到,参数更少了,在learning的时候 "学习空间"就小了很多。如果我们想从数据从学习这种distribution,参数多的话所需要的数据就多。因为我们知道机器学习的本质其实就是从一些可能的函数组,函数空间中,找到最好的那个。(这个最好的定义可以很丰富cost function之类的)。再往深处想,为什么我们可以讲"学习空间"从原来的2^n 讲到 n, 是因为我们知道了一条很有用的信息:"变量间的关系",根据信息论的原理,很显然,这条信息有助于将我们的原来的模型不确定性减少很多。具体倒数学公式上就是它已经讲那个原本未知的distribution函数表达成了乘积的形式,我们从原本未知,到知道了函数的结构,这是一个很大的进步。
通过这个例子的学习。我们大概就猜到了representation 这一章应该会在只根据变量间的 independence properies, 来给出compact(所需要independent parameter少) 的表示。因为compac的表示易于处理和learning。
核心主题: How independece properties can be used to the represent the high-dimension distribution much more compactly.
二、CPD -- An alternative parameterization of distribution
1、利用信息:causality

2、parameterization 方式: prior distribution over the ancestors + conditional distribution CPD over the chidren given P
假设 scope of Difficulty is {d0 (不难),d1}、Intellgence scope 的大小为2,Grade 的大小为3。
则navie 的表示需要的indepedent parameter 数为12.
而采用CPD
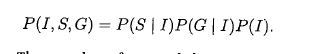
所学的independent parameter 数为 7 = 1+2+4
3、额外优点:modularity
when given G, only need to construct CPD P(G|I).
4、例子:navie bayesian model
结构如下.

应用场合:

缺点:忽略了feature variable间的相互关系。如果feature variable 之间存在相互关系,则用来计算P(C|X1,X2,..)的时候会偏大。
三、贝叶斯网络(Bayesian Network)
1、首先我们要明白贝叶斯网络是干嘛的,我们为什么需要它。
在上面的段落我们已经分析过了CPD是一种利用变量间的causality的 compact representation。现在我想表达如下变量间的这种条件依赖关系,我会怎么表达呢?
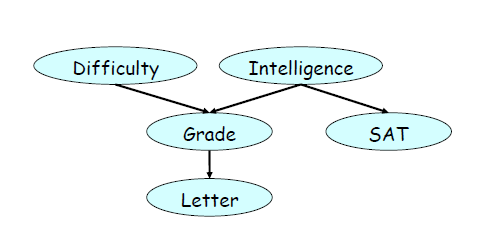
(1)用一大堆文字
(2)Factorization的方式:

(3)conditional independent statements:
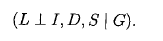
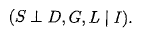
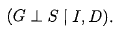
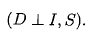
我们现在我们对为什么我们会引入贝叶斯网络有一个直观的了解了。以为他就是表达变量间的联系的很自然的模型啊。
2、正式定义
其实,有了上面的分析我们知道贝叶斯网络就是用来一种用来表示变量间条件独立以及存在明显的causality的表达方式。没有什么多牛逼的,我们自己也可以试着来定义贝叶斯网络模型。所为定义贝叶斯网络,就是给这个数学意义上的图赋予我们希望有的"涵义"(sematics)。
(1)基本结构:有向图。因为我们要表达的是一种变量之间存在causality关系的distribution。
(2)定义语义(sematic)节点 : random variabl。边:A--->B B和其兄弟,given A,条件独立。
接下来我们给出教材中的定义。哈,是不是差不多。

3、有了上面的定义,我们可以看到给了我们一个BN,其实在给了我们两个东西。
(1)factorization
(2)set of conditional dependency
其实这两个东西是等价的。为了更好的描述问题,我们引路了Imap 和 Factorize的概念。
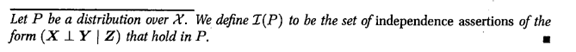

要证明也很简单:

本质上就是利用条件独立定义来证明。没有什么可说的。