逻辑回归
假设在自变量X1,X2,..Xn作用下,某事件发生的概率为p,则该事件不发生的概率为1-p ,p/(1-p) 为发生的概率和不发生的概率之比,记做优势odds 若对odds取自然对数,得到
 称为P的logit变换,
称为P的logit变换,
则logistic回归模型为:
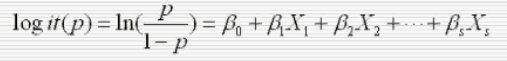
则概率计算公式为
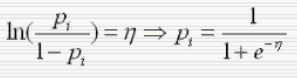
没有连续的值的情况称作哑变量
当自变量X是离散型变量时,SAS自动将其设为哑变量,根据X的水平数的不同,如X有水平数N,则相应的哑变量有N-1个

| 赢 | 输 | |
| 德国 | 60 | 20 |
| 巴西 | 90 | 10 |
德国赢得概率:60/80=0.75
德国输的概率:20/80 =0.25
德国的odds :0.75/0.25=3 同理 巴西的odds = 0.9/0.1 =9
巴西对德国的odds ratios = 3/1

哑变量和odds
proc logistic data = lg.b_sales_inc; class gender (param=ref ref = "Male") income(param =ref ref = "Low"); model purchase(event='1')=gender/ selection=backward; run;
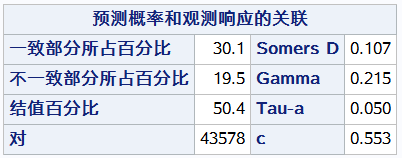
总配对数 :1的个数有多少个乘以0的个数有多少个
percent Concordant(一致部分所占百分比):预测1的概率大于0的概率的配对数占总配对数的比
percent Discordant(不一致部分所占百分比):预测1的概率小于0的概率的配对数占总配对数的比
percent Tied(结值百分比):预测1的概率等于0的概率的配对数占总配对数的比
pairs(对):所有1的个数乘以所有0的个数即总配对数
c统计量 :percent Concordant + percent Tied/2
一致性比率percent concordant越大 说明预测值与观测值在现有水平上有较强的关联性,回归模型有很强的预测能力。