关于输出多个LCS(最长公共子序列)的简单技巧
百度百科:
一个序列 S ,如果分别是两个或多个已知序列的子序列,
且是所有符合此条件序列中最长的,则 S 称为已知序列的最长公共子序列。
注意:S在已知序列中可以不连续;比如ABCBDAB和BDCABA的LCS为BCBA,BCBA不连续出现。
LCS通常利用动态规划算法求解,最简单的求解方式如《算法导论》所述:
1.设输入为X1X2…Xm,Y1Y2…Yn,构造二维数组B、C;
其中B[i][j]存储C[i][j]的最优解指向,C[i][j]存储X[1…i]和Y[1…j]的LCS长度;
2.B、C数组同时更新:
2.1.令B[0][k]、C[0][k](k=0…n)和B[k][0]、C[k][0](k=0…m)为0;
2.2.按下标从小到大的顺序依次计算每行的B[i][j]和C[i][j],规则如下:
①.若X[i]=Y[j],则C[i][j]=C[i-1][j-1]+1,B[i][j]=0;
②.若X[i]!=Y[j],则C[i][j]=Max(C[i][j-1],C[i-1][j]),B[i][j]=1或2;
3.更新完B、C后,从C[m][n]开始递归输出,根据B[i][j]的指向打印LCS;
相信大家都明白这个原理,简单的用一张图来说明一下:
1.箭头代表B[i][j]的值,其中用指向左上方的箭头代表0,←和↑代表1和2(或2和1);
2.箭头下方的数字为C[i][j]的值,即子问题X[1…i]和Y[1…j]的LCS长度;
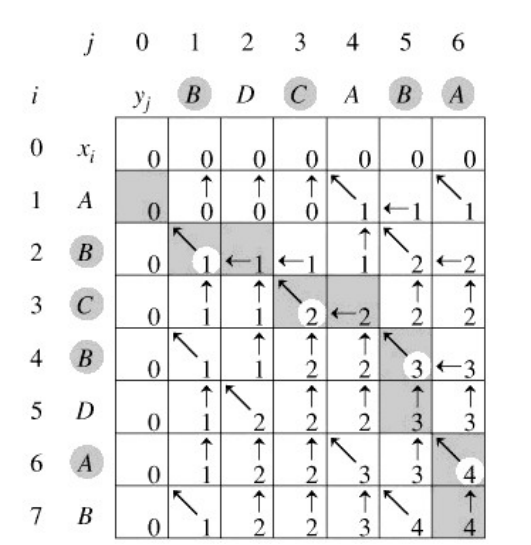
可是这样的构造只能输出一个LCS,但是我们发现BCBA、BCAB、BDAB都是该序列集的LCS。
为什么呢?因为该算法在C[i-1][j]=C[i][j-1]时,只记录了一种情况!即没有保存分支!
如何简单的修改算法,以求得多个LCS呢?下面介绍一种改进的方法。
还是利用数组B、C,并且C的计算规则不变,下面修改B的计算规则:
1.若X[i]=Y[j],B[i][j]=0;
2.若X[i]!=Y[j],有以下判断:
①.若C[i-1][j]>C[i][j-1],则C[i][j]=C[i-1][j],B[i][j]=1;
②.若C[i-1][j]<C[i][j-1],则C[i][j]=C[i][j-1],B[i][j]=2;
③.若C[i-1][j]=C[i][j-1],则C[i][j]的长度任取,B[i][j]=3;
此时用另一张图表示该算法:
1.用四种箭头表示B[i][j]的值,其中←和↑都存在时,表示C[i-1][j]=C[i][j-1];
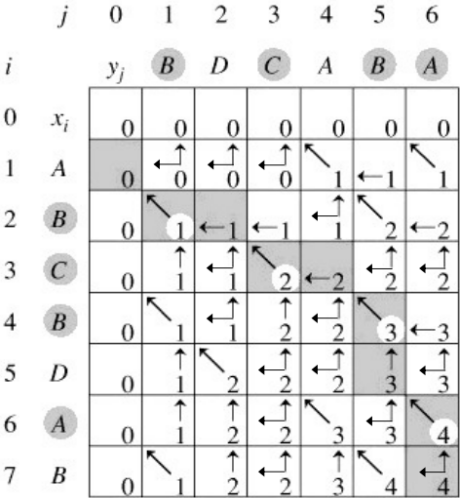
2.输出的时候采用正则表达式的思想:遇到B[i][j]=3时,同时对两种情况进行递归;
形式为“(←+↑)”,其中←和↑分别表示两个子问题的LCS;
补充:(A+B),在正则表达式中意义为A或B,即“+”表示二选一的关系。
下面给出C++源代码帮助大家更好地理解:(编译器为Codeblocks)
1 #include<iostream>
2 #include<string.h>
3 #define M 100
4 #define N 100
5 using namespace std;
6
7 void LCS_length(string x,string y,int B[M][N],int C[M][N])/*动态规划*/
8 { for(int i=1;i<=x.length()-1;i++) C[i][0]=0;
9 for(int j=0;j<=y.length()-1;j++) C[0][j]=0;
10 for(int i=1;i<=x.length()-1;i++)
11 for(int j=1;j<=y.length()-1;j++)
12 { if(x[i]==y[j])
13 { C[i][j]=C[i-1][j-1]+1;B[i][j]=0/*Up&Left*/;}
14 else if(C[i-1][j]>C[i][j-1])
15 { C[i][j]=C[i-1][j];B[i][j]=1/*Up*/;}
16 else if(C[i-1][j]<C[i][j-1])
17 { C[i][j]=C[i][j-1];B[i][j]=2/*Left*/;}
18 else
19 { C[i][j]=C[i][j-1];B[i][j]=3/*Up+Left*/;}}}
20
21 void Print_LCS(string x,int B[M][N],int i,int j)/*输出LCS*/
22 { if(!i||!j) return;
23 if(!B[i][j])
24 { Print_LCS(x,B,i-1,j-1);cout<<x[i];}
25 else if(B[i][j]==1)
26 Print_LCS(x,B,i-1,j);
27 else if(B[i][j]==2)
28 Print_LCS(x,B,i,j-1);
29 else
30 { cout<<'(';
31 Print_LCS(x,B,i-1,j);
32 cout<<'+';
33 Print_LCS(x,B,i,j-1);
34 cout<<')';}}
35
36 int main()
37 { string x,y;
38 cin>>x;cin>>y;
39 x=' '+x;y=' '+y;
40 int B[M][N],C[M][N];
41 LCS_length(x,y,B,C);cout<<endl;
42 Print_LCS(x,B,x.length(),y.length());}
可以在https://github.com/XueDingWen/Software-Security/blob/master/LCS.cpp下载
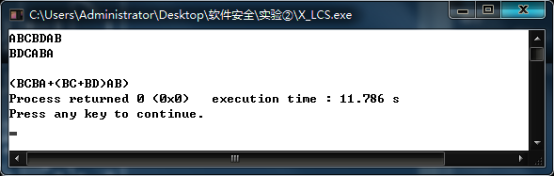
看完Print_LCS()函数,大家应该大致有所了解,下面给出运行结果:
输入为ABCBDAB、BDCABA;
输出为(BCBA+(BC+BD)AB),即表示BCBA、BCAB、BDAB都为输入的LCS;
当然,如果不想采用这种形式,也可以:
1.用字符型数组(如Vector)或String型变量保存输出;
2.根据括号分解,输出多个LCS;
还有一种方式:
1.遍历数组B,用栈保存B[i][j]=3的点的坐标,比如[7,6],[5,3]等;
2.让这些点的赋值从11……11逐渐变为22……22;
因为B[i][j]=3可以理解为B[i][j]=1或2,那么用二进制序列的思想遍历每种赋值情况;
当然此时时间开销更大,还可能重复输出,所以建议第一种方式。
