烟囱是一个3*3的中空构造,给定烟囱的高度,问用1*1*2的砖头搭成这个烟囱有多少种方法。
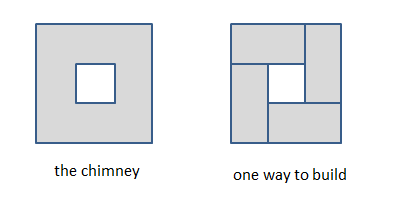
首先用一个8位二进制数表示某一层的状态。枚举上下两层的状态,判断这两个状态是否可以相邻,上一层必须将下层填满,但是上层自身可以有空格。当下层为0时,上层必须为1,表示放一个竖着的矩形块,因此必须满足up_stat|low_stat=255,上层中除了竖着的砖头,都是单个或连续个横放的砖头,所以必须满足up_stat&low_stat中的连续1都是偶数个。注意循环的问题,比如0的位置是1,7位置也是1,而实际上0和7是相邻着的。
相邻层的状态会构造出一个矩阵表示转化关系,为0时代表不能相邻,否则该值表示转化方法数,注意当low_stat=up_stat=255时,会有两种情况,其它的状态都是一种情况。
因为状态较多,即使使用矩阵乘法加速,复杂度也是很高的,交上去果然是超时了。仔细一想,第一层的状态必须是255,中间有很多状态实际上无用的,比如有奇数个1的状态,这些状态根本就是不可达的,于是以255为第一层搜索了一下,果然有用的状态只有70个。复杂度为70^3*log(10^9),优化一下大概跑1秒左右。
1 #include <string.h> 2 #include <stdio.h> 3 #define MOD 1000000007 4 #define MAXN 71 5 typedef __int64 LL; 6 int cas,n; 7 int dmat[MAXN][MAXN],id[256],ids; 8 struct matrix{ 9 int mz[MAXN][MAXN]; int n,tmp_cal[35]; 10 #define FOR(i) for(int i=1;i<=n;i++) 11 //初始化矩阵,空矩阵,单位矩阵和dmat矩阵 12 void init(int nn,int type){ 13 memset(tmp_cal,0,sizeof tmp_cal);n=nn; 14 if(type==0)FOR(i)FOR(j)mz[i][j]=0; 15 else if(type==1)FOR(i)FOR(j)mz[i][j]=(i==j)?1:0; 16 else FOR(i)FOR(j)mz[i][j]=dmat[i][j]; 17 } 18 matrix operator *(const matrix& b){ 19 matrix ans;ans.init(n,0); 20 FOR(i)FOR(j)if(mz[i][j])FOR(k) 21 ans.mz[i][k]=(ans.mz[i][k]+(LL)mz[i][j]*b.mz[j][k])%MOD; 22 return ans; 23 } 24 matrix binMat(int x); 25 }tmp[35],m; 26 matrix matrix::binMat(int x){ 27 if(!tmp_cal[0]){tmp_cal[0]=1,tmp[0].init(n,2);} 28 matrix ans;ans.init(this->n,1); 29 for(int i=0;x;x>>=1,i++){ 30 if(x&1)ans=ans*tmp[i]; 31 if(!tmp_cal[i+1])tmp_cal[i+1]=1,tmp[i+1]=tmp[i]*tmp[i]; 32 } 33 return ans; 34 } 35 //判断是否可接的条件,或的结果为1<<8-1,与的结果中没有连续的奇数个1 36 int cango(int p1,int p2){ 37 if((p1|p2)!=255)return 0; 38 p1=p1&p2;if(p1==255)return 1; 39 while(p1&1)p1=1<<7|(p1>>1); 40 for(int i=0,d=0;i<9;i++) 41 if(i<8&&(p1>>i)&1)d++; 42 else if(d&1)return 0; 43 return 1; 44 } 45 void dfs(int p){ 46 if(!id[p])id[p]=++ids; 47 for(int i=0;i<256;i++){ 48 if(cango(p,i)){ 49 if(id[i]==0)dfs(i); 50 dmat[id[p]][id[i]]=1; 51 } 52 } 53 } 54 void init(){ 55 ids=0; 56 dfs(255); 57 dmat[id[255]][id[255]]=2; 58 m.init(ids,2); 59 } 60 int main(){ 61 init(); 62 scanf("%d",&cas); 63 for(int ca=1;ca<=cas;ca++){ 64 scanf("%d",&n); 65 printf("Case %d: %d\n",ca,m.binMat(n).mz[1][1]); 66 } 67 }