[Codeforces Round #248 (Div. 2)] B. Kuriyama Mirai's Stones

B. Kuriyama Mirai's Stones

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Kuriyama Mirai has killed many monsters and got many (namely n) stones. She numbers the stones from 1 to n. The cost of the i-th stone is vi. Kuriyama Mirai wants to know something about these stones so she will ask you two kinds of questions:

1. She will tell you two numbers, l and r (1 ≤ l ≤ r ≤ n), and you should tell her .
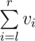2. Let ui be the cost of the i-th cheapest stone (the cost that will be on the i-th place if we arrange all the stone costs in non-decreasing order). This time she will tell you two numbers, l and r (1 ≤ l ≤ r ≤ n), and you should tell her .

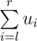For every question you should give the correct answer, or Kuriyama Mirai will say "fuyukai desu" and then become unhappy.

Input

The first line contains an integer n (1 ≤ n ≤ 10^5). The second line contains n integers: v1, v2, ..., vn (1 ≤ vi ≤ 10^9) — costs of the stones.

The third line contains an integer m (1 ≤ m ≤ 10^5) — the number of Kuriyama Mirai's questions. Then follow m lines, each line contains three integers type, l and r (1 ≤ l ≤ r ≤ n; 1 ≤ type ≤ 2), describing a question. If type equal to 1, then you should output the answer for the first question, else you should output the answer for the second one.

Output

Print m lines. Each line must contain an integer — the answer to Kuriyama Mirai's question. Print the answers to the questions in the order of input.

Sample test(s)

input

6
6 4 2 7 2 7
3
2 3 6
1 3 4
1 1 6

output

24
9
28

input

4
5 5 2 3
10
1 2 4
2 1 4
1 1 1
2 1 4
2 1 2
1 1 1
1 3 3
1 1 3
1 4 4
1 2 2

output

10
15
5
15
5
5
2
12
3
5

Note

Please note that the answers to the questions may overflow 32-bit integer type.

题解：维护两个前缀和，原序sum1[]和有序sum2[],因为n (1 ≤ n ≤ 10^5)，(1 ≤ vi ≤ 10^9) ，所以n*v<=10^14，所以sum[]为long long 类型即可。剩下的m次询问，每次运行时间复杂度就为O(1),然后本题就得到解决。

代码：

#include<stdio.h>
#include<string.h>
#include<stdbool.h>
#include<stdlib.h>
#include<math.h>
#include<ctype.h>
#include<time.h>

#define rep(i,a,b)  for(i=(a);i<=(b);i++)
#define red(i,a,b)  for(i=(a);i>=(b);i--)
#define sqr(x)      ((x)*(x))
#define clr(x,y)    memset(x,y,sizeof(x))
#define LL          long long


int i,j,n,m,
    a[110000];

LL sum1[110000],sum2[110000];

void pre()
{
    clr(a,0);
    clr(sum1,0);
    clr(sum2,0);
}

void sort(int head,int tail)
{
    int i,j,x;
    i=head;j=tail;
    x=a[head];
    
    while(i<j)
    {
        while((i<j)&&(a[j]>=x)) j--;
        a[i]=a[j];
        while((i<j)&&(a[i]<=x)) i++;
        a[j]=a[i];
    }
    
    a[i]=x;
    
    if(head<(i-1)) sort(head,i-1);
    if((i+1)<tail) sort(i+1,tail);
}

int init()
{
    int i;
    scanf("%d",&n);
    rep(i,1,n){
        scanf("%d",&a[i]);
        sum1[i]=sum1[i-1]+a[i];
    }
    sort(1,n);
    
    rep(i,1,n)
        sum2[i]=sum2[i-1]+a[i];
    return 0;
}

int main()
{
    int i,ty,x,y;
    pre();
    init();
    
    scanf("%d",&m);
   
    rep(i,1,m){
        scanf("%d%d%d",&ty,&x,&y);
        if(ty==1) printf("%lld
",sum1[y]-sum1[x-1]);
        else printf("%lld
",sum2[y]-sum2[x-1]);
    }
   
    return 0;
}