1. 堆的概念
堆的数据结构是一种数组对象;堆可以视作为一颗完全二叉树(其中,树的每一层都填满,最后一层可能除外);树中每个节点与数组中存放该节点值的元素对应;
堆可以划分为两类:
a) 最大堆:除了根节点,有A[parent(i)] >= A[i],最大元素即根节点;
b) 最小堆:除了根节点,有A[parent(i)] <= A[i],最小元素即根节点;
对于给定节点i,可以根据其在数组中的位置求出该节点的父亲节点PARENT(i)=i/2、左孩子LEFT(i) = 2*i和右孩子RIGHT(i) = 2*i+1节点,这三个过程一般采用宏或者内联函数实现。
1 #define LEFT(i) (2 * i) 2 #define RIGHT(i) (2 * i + 1)
把堆看成一个棵树,有如下的特性:
a) 含有n个元素的堆的高度是lgn。
b) 当用数组表示存储了n个元素的堆时,叶子节点的下标是n/2+1,n/2+2,……,n
c) 在最大堆中,最大元素该子树的根上;在最小堆中,最小元素在该子树的根上。
2. 堆排序
划分为三块:保持堆性质、创建堆、排序;
1) 保持堆性质
通过MAX_HEAPIFY()函数,使得堆把持最大堆的性质,即除了根节点,有A[parent(i)] >= A[i],具体如下:
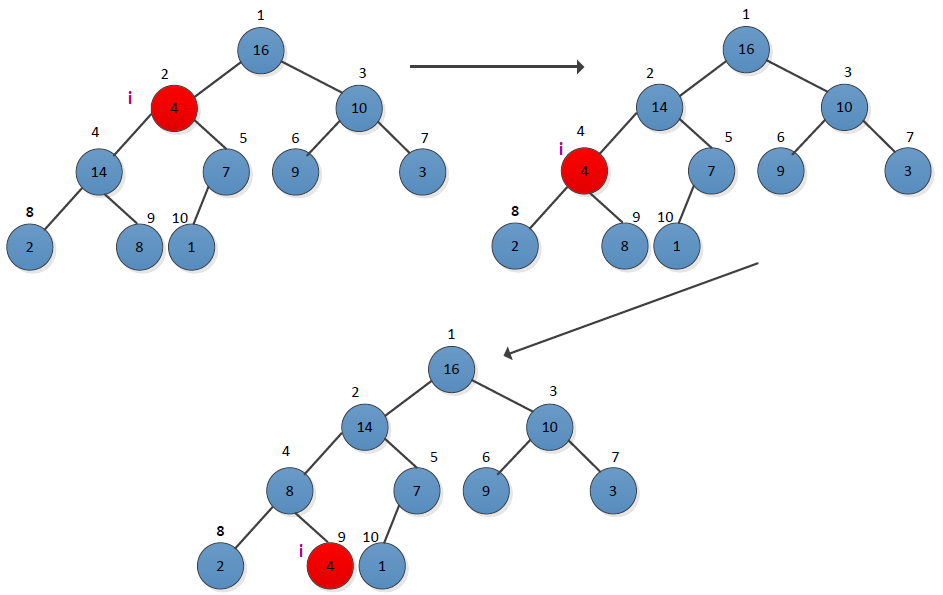
以MAX_HEAPIFY(A, 2)为例:
i = 2, l = 4, r = 5
14 > 4, 此时largest = 4
7 < 14, 此时largest仍为4
i(2) != largest(4),交换A[i](4)和A[largest](14)
递归调用MAX_HEAPIFY(A, largest)
函数如下:
1 void MAX_HEAPIFY(int A[], int i){ 2 int l = LEFT(i);//编号为i的左孩子编号l 3 int r = RIGHT(i);//编号为i的右孩子编号r 4 5 int largest;//存最大元素的下标 6 7 if((l <= MAXSIZE) && (A[l - 1] > A[i - 1])){//左孩子大于根节点 8 largest = l; 9 } 10 else{ 11 largest = i; 12 } 13 14 if((r <= MAXSIZE) && (A[r - 1] > A[largest - 1])){////右孩子大于上步求的较大节点 15 largest = r; 16 } 17 18 if(largest != i){//Exchange 19 int tmp = A[i - 1]; 20 A[i - 1] = A[largest - 1]; 21 A[largest - 1] = tmp; 22 23 MAX_HEAPIFY(A, largest);//递归确定以largest为根的堆是最大堆 24 } 25 }
其中,T(n) = O(lgn)
2) 创建最大堆
从最后一个非叶子节点(n/2)开始从底向上调用MAX_HEAPIFY确保最大堆。调整过程如下图所示:

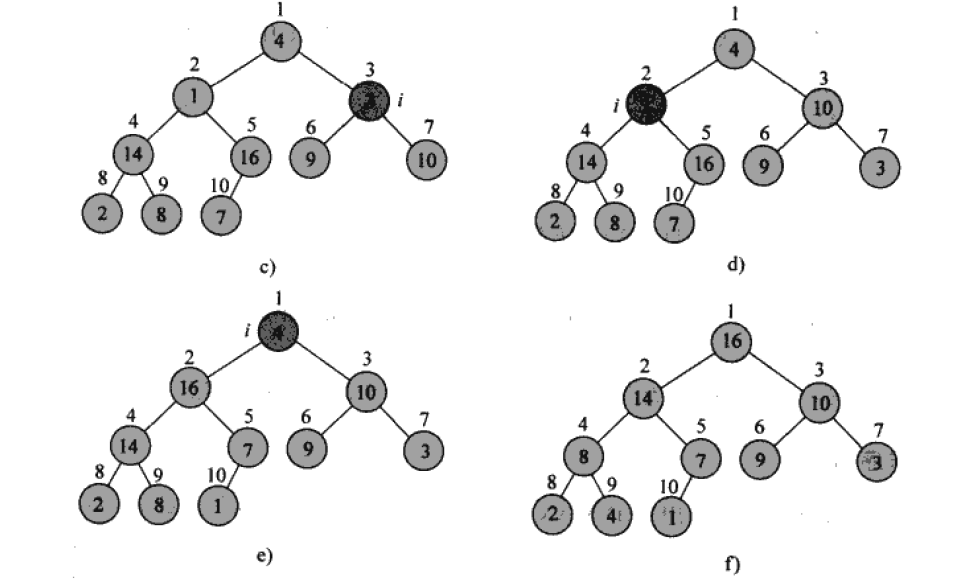
开始i = 10/2 = 5,从5到1每个节点处分别调用MAX_HEAPIFY,确保最大堆;
T(n)=O(n)
void BUILD_MAX_HEAP(int A[]){ //最后一个非叶子节点 int length = MAXSIZE / 2; int i; for(i = length; i > 0; i--){ MAX_HEAPIFY(A, i); } }
至此,可以建立最大堆,运行截图如下: