ZhongHaoxi P105-3 洗衣

Description

描述

洗完衣服，就要晒在树上。但是这个世界并没有树，我们需要重新开始造树。我们一开始拥有 $T_0$，是一棵只有一个点的树，我们要用它造出更多的树。
生成第i棵树我们需要五个参数 $a_i,b_i,c_i,d_i,l_i(a_i,b_i<i)$。我们生成第$i$棵树是将第 $a_i$ 棵树的 $c_i$ 号点和第 $b_i$ 棵树的 $d_i$ 号点用一条长度为 $l_i$ 的边连接起来形成的新的树（不会改变原来两棵树）。下面我们需要对新树中的点重编号；对于原来在第 $a_i$ 棵树中的点，我们不会改变他们的编号；对于原来在第 $b_i$ 棵树中的点，我们会将他们的编号加上第 $a_i$ 棵树的点的个数作为新的编号。
定义
$$ F(T_i) = sum_{i=0}^{n-1} sum_{j=i+1}^{n-1} d(v_i, v_j)$$
其中，$n$ 为树 $T_i$ 的大小，$v_i,v_j$ 是 $T_i$ 中的点，$d(v_i,v_j)$ 代表这两个点的距离。现在希望你求出 $∀1≤i≤m,F(T_i)$ 是多少。

输入

第一行一个整数 $m$，代表要造多少棵树。

接下来 $m$ 行，每行 $5$ 个数 $a_i,b_i,c_i,d_i,l_i$。

输出

$m$ 行每行一个整数代表 $F(T_i)$ 对 $10^9+7$ 取模之后的值。

样例

输入

3
0 0 0 0 2
1 1 0 0 4
2 2 1 0 3

输出

2
28
216

约定

对于 $30\%$ 的数据，$1≤m≤10$。

对于 $60\%$ 的数据，每棵树的点数个数不超过 $10^5$。

对于 $100\%$ 的数据，$1≤m≤60$。

Solution

让我们用$ans_i$表示第$i$次操作的答案，不难想到 $ans_i = ans_{a_i} + ans_{b_i} + dots$

那么后面还要加什么呢？

 举个例子

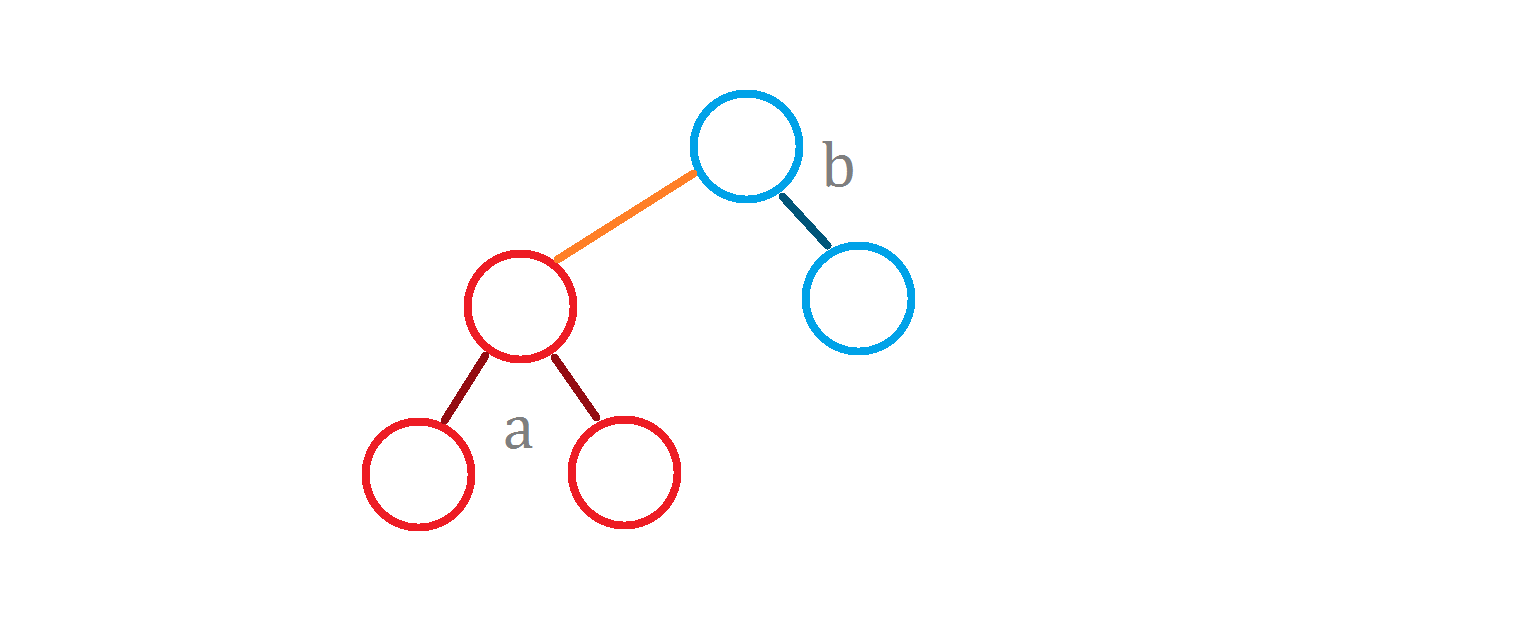
 红色的为 $a$ ，蓝色的为 $b$ ，橙色的为这次连接的长度为 $l$ 的边。

既然两棵子树内部的答案都已经统计了，我们只需要统计跨 $l$ 的答案即可。

首先考虑 $l$ 的贡献，因为 $a$ 和 $b$ 中的每一个节点都会记录一次答案，所以 $l$ 经过了 $size_a imes size_b$ 次。

然后，我们显然可以用 $sum_{i=0}^{size_a - 1} sum_{j = 0}^{size_b - 1} ( operatorname{dist}(i, c) + operatorname{dist}(j, d)) $，来表示剩余的答案，化简一下：

 $sum_{i=0}^{size_a - 1} sum_{j = 0}^{size_b - 1} ( operatorname{dist}(i, c) + operatorname{dist}(j, d)) $

$= sum_{i=0}^{size_a - 1} (sum_{j = 0}^{size_b - 1} operatorname{dist}(i, c) + operatorname{g}(b, d))$

$= sum_{i=0}^{size_a - 1} sum_{j = 0}^{size_b - 1} operatorname{dist}(i, c) + sum_{i=0}^{size_a - 1}operatorname{g}(b, d)$

$= sum_{j = 0}^{size_b - 1} operatorname{g}(a, c) + sum_{i=0}^{size_a - 1}operatorname{g}(b, d)$

$= operatorname{g}(a, c) imes size_b + operatorname{g}(b, d) imes size_a$

 其中 $operatorname{g}(T, u)$ 表示在 $T$ 这棵树中，$u$ 这个节点到其它所有节点的距离和。

于是就可以愉快的计算答案啦。

int main()
{
	ios::sync_with_stdio(false);
	cin >> m;
	for(register int i = 1; i <= m; i++)
	{
		cin >> a[i] >> b[i] >> c[i] >> d[i] >> l[i]; 
	}
	size[0] = 1;
	for(register int i = 1; i <= m; i++)
	{
		// 先递推 size[] 
		size[i] = (size[a[i]] + size[b[i]]) % MOD;
	}
	for(register int i = 1; i <= m; i++)
	{
		// 计算 ans[] 并输出 
		ans[i] = ((ans[a[i]] + ans[b[i]]) % MOD + size[a[i]] * size[b[i]] % MOD * l[i] % MOD) % MOD;
		ans[i] = (ans[i] + g(a[i], c[i]) * size[b[i]] % MOD + g(b[i], d[i]) * size[a[i]] % MOD) % MOD;
		cout << ans[i] << endl;
	}
	return 0;
}

怎么实现 $operatorname{g}()$ 呢？

递推当然是可以的，但必然需要 $mathcal{O}(n imes m)$ 的复杂度，而 $n$ 却高达 $2^{60}$，一种可行的方法是使用递归，只计算需要的，再加上记忆化，就变成 $log$ 了。

 再用刚才的例子

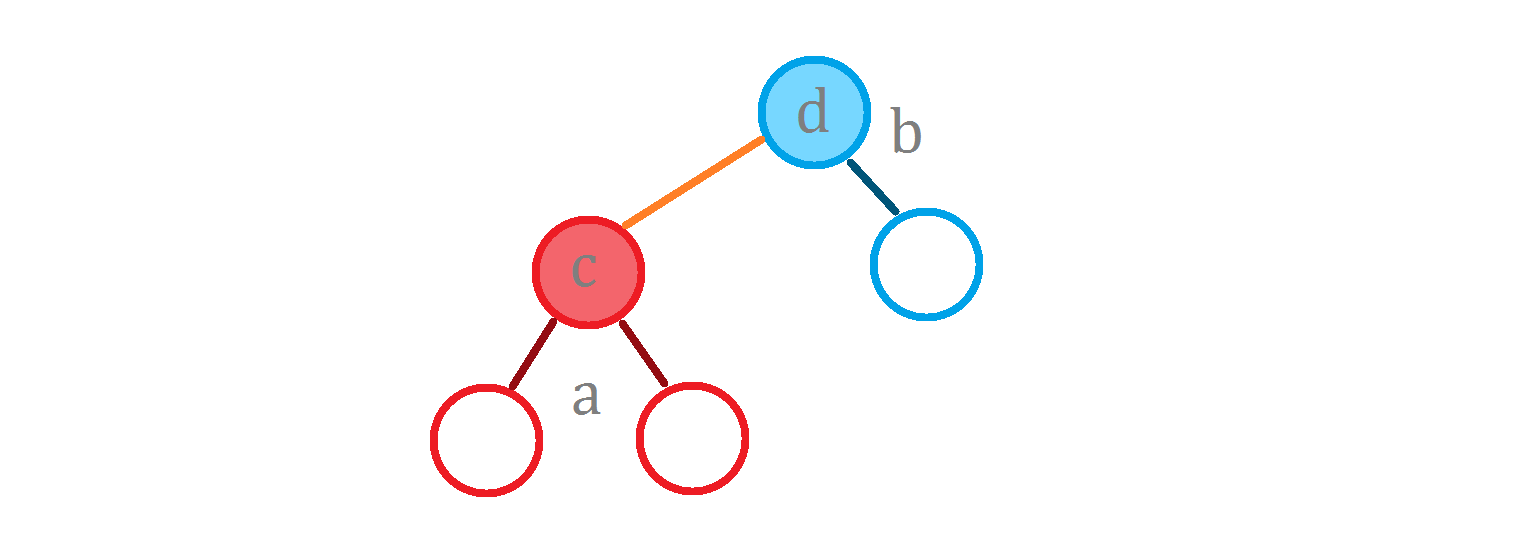
现在我们想要计算 $operatorname{g}(^* this, c)$。

其答案显然为：

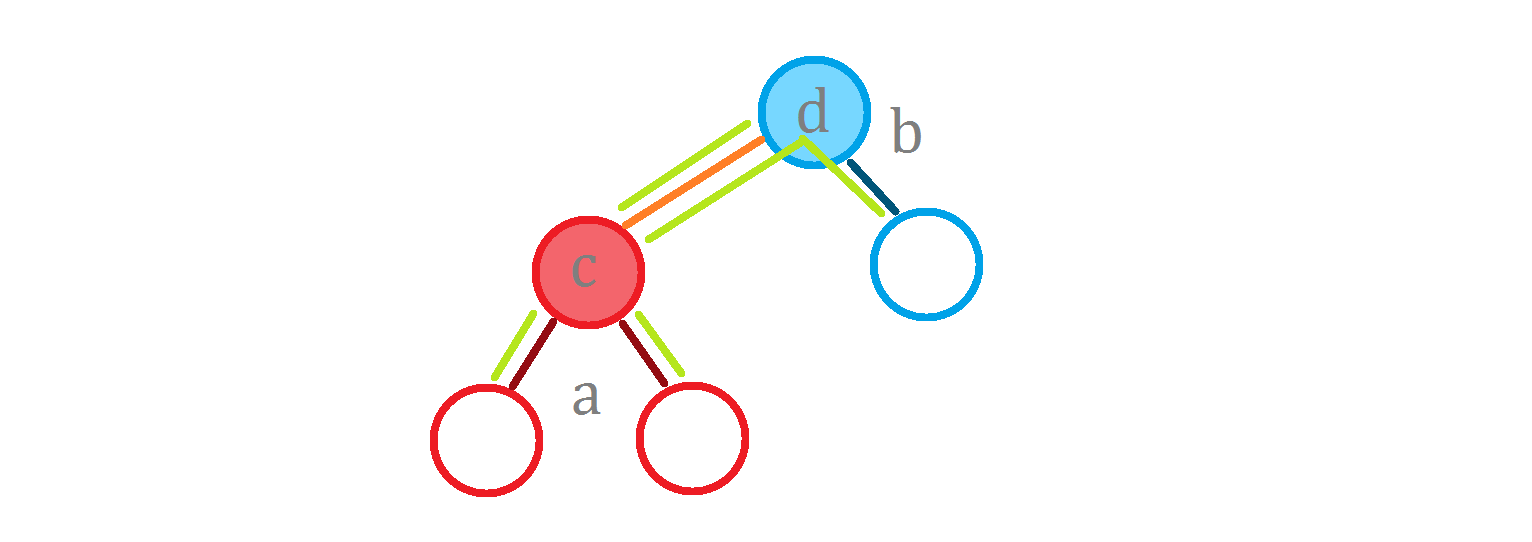
是不是就等于 $operatorname{g}(a, c) + operatorname{g}(b, d) + l imes size_b$？

那要是计算 $operatorname{g}(^* this, u)$ 呢？

 

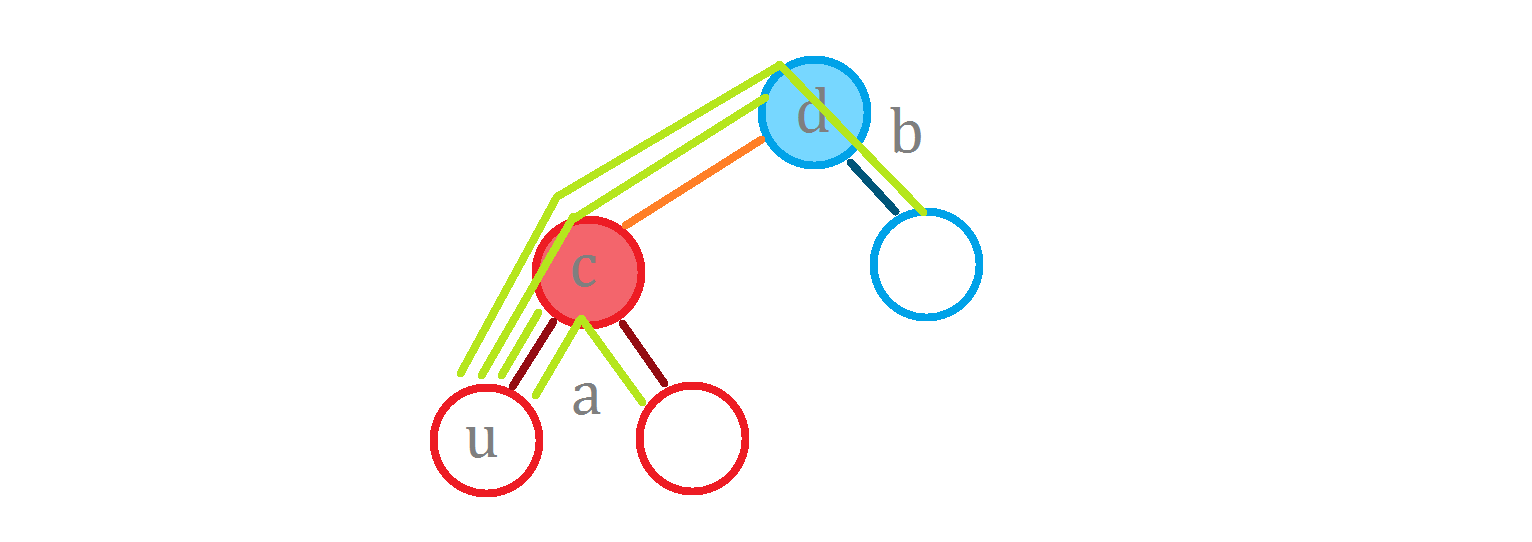
 要是按照刚刚的方法，计算 $operatorname{g}(a, c) + operatorname{g}(b, d) + l imes size_b$ 的话：

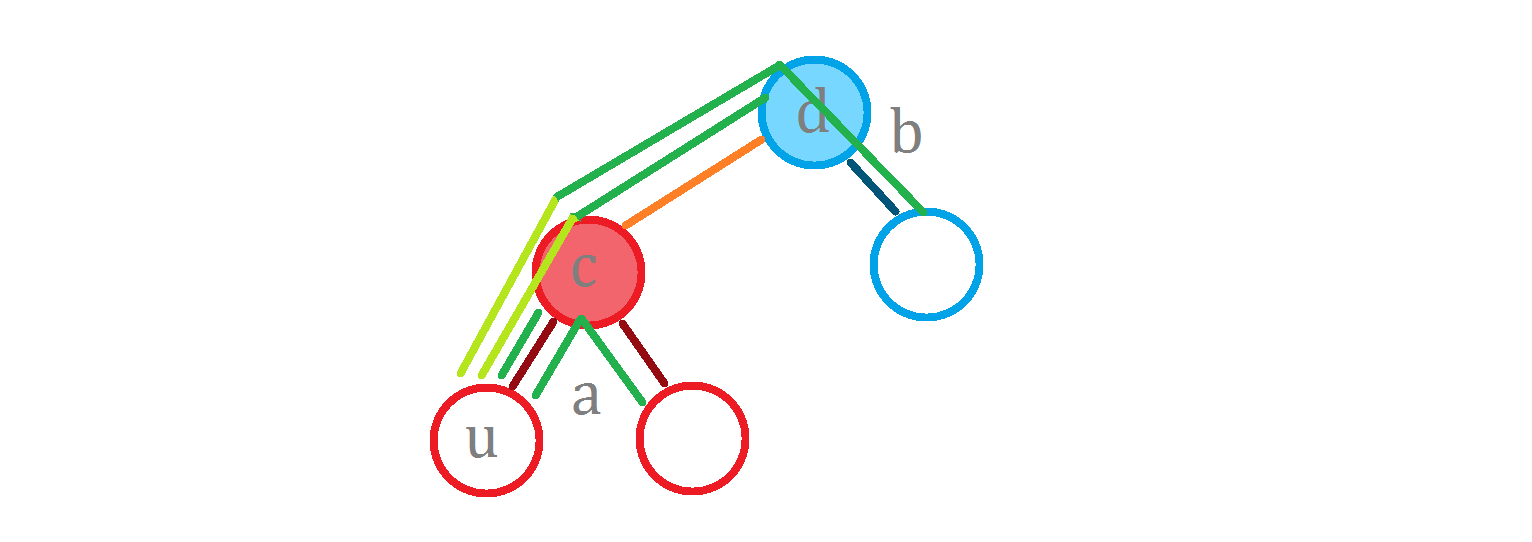
 漏掉的这个是什么？恰好就是 $size_b imes operatorname{dist}(a, u, c)$（这里的 $ operatorname{dist}$ 是指在 $a$  这棵子树中，$u$ 和 $c$ 的距离）。

于是：

$$ operatorname{g}(^* this, u)  = operatorname{g}(a, u) + operatorname{g}(b, d) + (l + operatorname{dist}(a, u, c)) imes size_b $$

$u$ 在 $b$ 中同理，注意 $u$ 的编号要减去 $size_a$。

LL g(LL id, LL pos)
{
	// map1 是记忆化映射 
	if(!id) return 0;
	pair<LL, LL> query = make_pair(id, pos);
	if(map1.count(query)) return map1[query]; // 调用老数据 
	LL npos = pos - size[a[id]];
	// 计算并记忆化 
	if(pos < size[a[id]])
		map1[query] = ((dist(a[id], c[id], pos) + l[id]) * size[b[id]] % MOD + g(b[id], d[id]) + g(a[id], pos)) % MOD;
	else
		map1[query] = ((dist(b[id], d[id], npos) + l[id]) * size[a[id]] % MOD + g(a[id], c[id]) + g(b[id], npos)) % MOD;
	return map1[query];	
}

问题又来了，$operatorname{dist}(T, u, v)$ 怎么算呢？

LCA？建树也需要时间。

考虑到我们拥有完整的建树过程，而且树的种类至多 $60$ 种，那么当然可以递归来求啦。

也就是分类讨论一下：

1. 如果 $u, v$ 在 $T$ 的同一个子树 $child$ 中，显然 $operatorname{dist}(T, u, v) = operatorname{dist}(child, u, v)$
2. 否则，就是两者到 $l$ 的距离和加上 $l$ 的长度，$operatorname{dist}(T, u, v) = operatorname{dist}(child1, u, c) + operatorname{dist}(child2, v, d) + l$

同样注意 $b$ 那棵树里的节点编号要减去 $size_a$。

LL dist(LL id, LL pos1, LL pos2)
{
	if(!id || pos1 == pos2) return 0;
	pair<LL, pair<LL, LL> > query = make_pair(id, make_pair(pos1, pos2));
	if(map2.count(query)) return map2[query];
	if(pos1 < size[a[id]]) // pos1 在 a 中 
	{
		if(pos2 < size[a[id]]) map2[query] = dist(a[id], pos1, pos2); // pos2 也在 a 中 
		else map2[query] = (dist(a[id], pos1, c[id]) + dist(b[id], pos2 - size[a[id]], d[id]) + l[id]) % MOD; // pos2 在 b 中 
	}
	else // pos1 在 b 中 
	{
		if(pos2 < size[a[id]]) map2[query] = (dist(a[id], pos2, c[id]) + dist(b[id], pos1 - size[a[id]], d[id]) + l[id]) % MOD; // pos2 在 a 中 
		else map2[query] = dist(b[id], pos1 - size[a[id]], pos2 - size[a[id]]); // pos2 在 b 中 
	}
	return map2[query];
}

上述两个函数的边界都非常显然，于是就愉快的解决了这道题

完整代码如下：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MOD = 1000000007LL;
const int N = 70;
map<pair<LL, LL>, LL> map1;
map<pair<LL, pair<LL, LL> >, LL> map2;

LL m, a[N], b[N], c[N], d[N], l[N], ans[N], size[N];

LL dist(LL id, LL pos1, LL pos2)
{
	if(!id || pos1 == pos2) return 0;
	pair<LL, pair<LL, LL> > query = make_pair(id, make_pair(pos1, pos2));
	if(map2.count(query)) return map2[query];
	if(pos1 < size[a[id]]) // pos1 在 a 中 
	{
		if(pos2 < size[a[id]]) map2[query] = dist(a[id], pos1, pos2); // pos2 也在 a 中 
		else map2[query] = (dist(a[id], pos1, c[id]) + dist(b[id], pos2 - size[a[id]], d[id]) + l[id]) % MOD; // pos2 在 b 中 
	}
	else // pos1 在 b 中 
	{
		if(pos2 < size[a[id]]) map2[query] = (dist(a[id], pos2, c[id]) + dist(b[id], pos1 - size[a[id]], d[id]) + l[id]) % MOD; // pos2 在 a 中 
		else map2[query] = dist(b[id], pos1 - size[a[id]], pos2 - size[a[id]]); // pos2 在 b 中 
	}
	return map2[query];
}
LL g(LL id, LL pos)
{
	// map1 是记忆化映射 
	if(!id) return 0;
	pair<LL, LL> query = make_pair(id, pos);
	if(map1.count(query)) return map1[query]; // 调用老数据 
	LL npos = pos - size[a[id]];
	// 计算并记忆化 
	if(pos < size[a[id]])
		map1[query] = ((dist(a[id], c[id], pos) + l[id]) * size[b[id]] % MOD + g(b[id], d[id]) + g(a[id], pos)) % MOD;
	else
		map1[query] = ((dist(b[id], d[id], npos) + l[id]) * size[a[id]] % MOD + g(a[id], c[id]) + g(b[id], npos)) % MOD;
	return map1[query];	
}

int main()
{
	ios::sync_with_stdio(false);
	cin >> m;
	for(register int i = 1; i <= m; i++)
	{
		cin >> a[i] >> b[i] >> c[i] >> d[i] >> l[i]; 
	}
	size[0] = 1;
	for(register int i = 1; i <= m; i++)
	{
		// 先递推 size[] 
		size[i] = (size[a[i]] + size[b[i]]) % MOD;
	}
	for(register int i = 1; i <= m; i++)
	{
		// 计算 ans[] 并输出 
		ans[i] = ((ans[a[i]] + ans[b[i]]) % MOD + size[a[i]] * size[b[i]] % MOD * l[i] % MOD) % MOD;
		ans[i] = (ans[i] + g(a[i], c[i]) * size[b[i]] % MOD + g(b[i], d[i]) * size[a[i]] % MOD) % MOD;
		cout << ans[i] << endl;
	}
	return 0;
}