归并排序

归并排序 3个高效排序算法中最好理解的一个

众所周知，(OI)界有(3)个高效的排序算法（时间复杂度都在(O(nlogn))左右）——分别是快排、堆排序、归并排序。其中最好理解的就是归并排序了。快排我们可以直接用STL，堆排和归并我们就要手打了。下面说说归并排序吧！

[ ext{1、算法核心} ]

归并的核心就在于二分以达到(O(nlog_2n))的时间复杂度。其实归并的过程看起来仍然像一棵二叉树（不过它是在线性空间中进行的）。我们将一个一维数组二分，通过一块一块的排序以达到想要的效果。只要我们将分开来的(log_2n)个小块内部排序，再通过指针的比较就能排序完整个线性数组。

[ ext{2、实现步骤(以从小到大为例)} ]

STEP.1

如上面所说的，将一维数组分开，分成每一个元素单独存在的区间(例如要排序([1,8])(一维数组下标(1)~(8)的元素)区间，分开所形成的即为区间([1,1])&([2,2])&……&([8,8]))我们很容易得出，在这些元素单独存在的区间都是有序区间(只有(1)个元素比什么？当然有序咯)。

STEP.2

然后我们把眼光放大，准备合并区间。于是我们将相邻的两个区间进行合并，且在合并过程中就把顺序排好。譬如我们把([1,1])和([2,2])合并成([1,2])，在这个过程中我们只需要比较哪个元素更小就排到前面去即可。当然还有更复杂的情况，比如将([1,2])和([3,4])合并成([1,4])，此时我们就不能简单地只判断一个元素了，此时如果还想排好序，我们需要一个简单的小道理：每个区间都是排好序的。这很重要，因为如果有两个区间：((4,5,7,9))、((2,3,6,8))。我们不难发现，就像两堆排好的扑克牌一样，我从头开始比较，较小的牌从顶端拿走，而第二次同样把更新后的较小的牌拿走，就肯定会形成一个有序序列。实际上归并的过程就是这样从两个区间各取头出来，实现一种堆叠式的排序。如果没看懂的话建议看图哦。

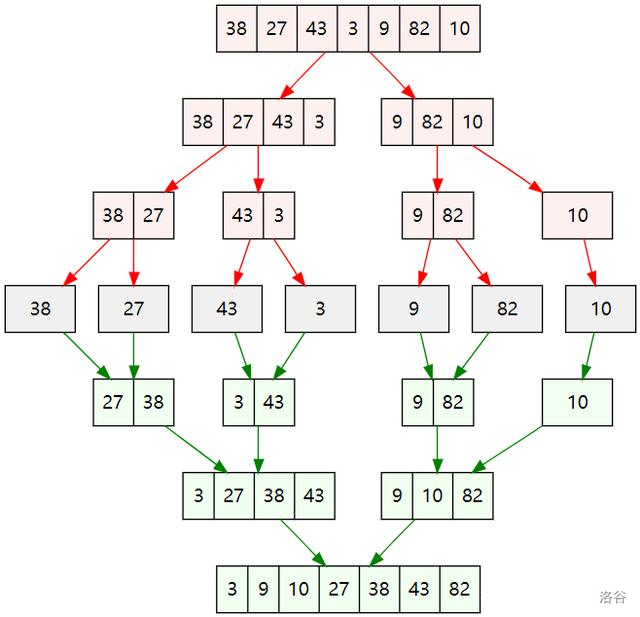
转自 网络

[ ext{3、奉上代码(快速排序模板)} ]

#include<iostream>
#include<cstdio>
#include<cstring>
#define N 1000001
#define r(a,b,c) for(int c=a;c<=b;++c)
using namespace std;
int a[N],r[N],ans,n;

void s(int l,int rr)
{
    if(l==rr)
	{
		return;
	}
	int mid=(l+rr)>>1;
	s(l,mid);
	s(mid+1,rr);
	int i=l,j=mid+1,k=l;
	while(i<=mid&&j<=rr)
	{
		if(a[i]<=a[j])
		{
			r[k++]=a[i++];
		}
		else
		{
			r[k++]=a[j++];
			ans+=mid-i+1;;
		}
	}
	while(i<=mid)
	{
		r[k++]=a[i++];
	}
	while(j<=rr)
	{
		r[k++]=a[j++];
		
	}
	r(l,rr,i)
	{
		a[i]=r[i];
	}
	return;
}

int main()
{
	cin>>n;
	r(1,n,i)
	{
		cin>>a[i];
	}
	s(1,n);
//	cout<<ans<<endl;
	r(1,n,i)
	{
		cout<<a[i]<<' ';
	}
	return 0;
}

好久以前打的代码，码风极丑，抱歉

填坑第(huge{7})站完成！