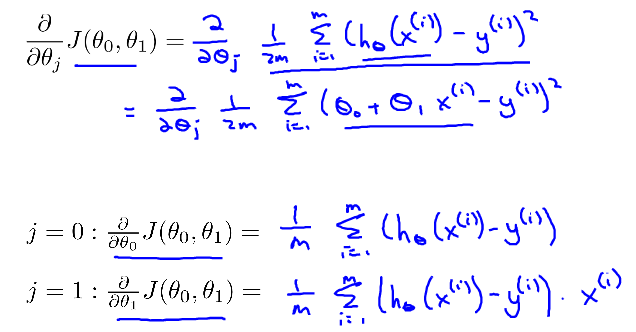1、模型描述
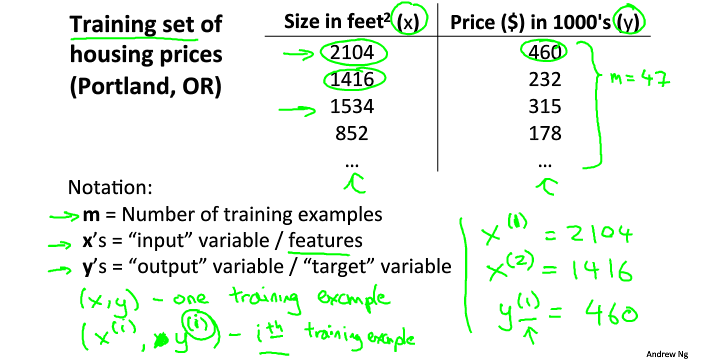
给定一组数据,如房屋的面积及其价格,根据给定的数据假设出一个模型,然后用来估计给定面积的房屋的价格。
m:训练样本的数量
x's:输入变量/特征
y's:输出变量/目标变量
(x,y):训练样本
(xi,yi):第i个训练样本,i表示样本中的第i行
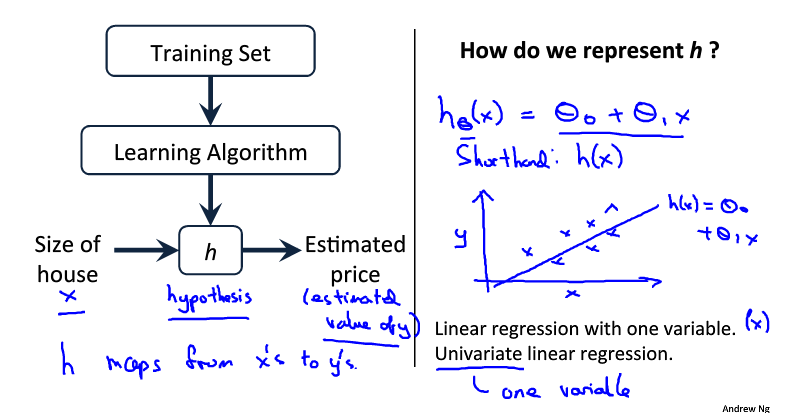
h(θ)=θ0+θ1x ; 是一个线性函数,类似于y=ax+b;单变量线性回归:即只有一个变量(特征)
h是一个假设函数(由x→y的映射)其作用是预测y是关于x的线性函数;x:特征/输入变量
2、代价函数
损失函数(Loss/Error Function):计算单个训练集的误差
代价函数(Cost Function):计算整个训练集所有损失函数之和的平均值
代价函数又叫平方误差函数或平方误差代价函数
代价函数为:![]()
目标函数为:![]()

为了直观理解代价函数到底是在做什么,先假设θ0=0,并假设训练集有三个数据,分别为(1,1),(2,2),(3,3)这样在平面坐标系中绘制出hθ(x),并分析J(θ0,θ1)的变化。

上图中右侧J(θ0,θ1)随着θ1的变化而变化,可见当θ1=1时,J(θ0,θ1)= 0,取得最小值,对应于左图青色直线,即函数h拟合程度最好的情况。
代价函数-直观理解
注:该部分由于涉及到了多变量成像,可能较难理解,要求只需要理解上节内容即可,该节如果不能较好理解可跳过。
给定数据集:

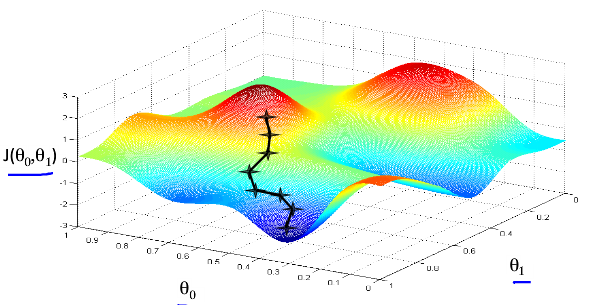
参数在θ0不恒为0时代价函数J(θ)关于θ0,θ1的3-D图像,图像中的高度为代价函数的值。

由于3-D图形不便于标注,所以将3-D图形转换为轮廓图(contour plot),下面用轮廓图(下图中的右图)来作直观理解,其中相同颜色的一个圈代表着同一高度(同一J(θ)值)。
θ0=360,θ1=0时:

大概在θ0=0.12,θ1=250时:

上图中最中心的点(红点),近乎为图像中的最低点,也即代价函数的最小值,此时对应 对数据的拟合情况如左图所示,嗯,一看就拟合的很不错,预测应该比较精准啦。
3、梯度下降
让计算机自动找出最小化代价函数时对应的θ值;
思想:开始的时候,随便选择一个参数组合(θ0,θ1,θ2......θn),即起始点,计算代价函数。然后寻找下一个能使得代价函数下降最多的 参数组合,不懂迭代,直到找到一个局部最小值。由于下降的情况只考虑当前参数组合周围的情况,所以无法确定当前的局部最小值是否就 是全局最小值。不同的参数组合,可能会产生不同的局部最优值。如下图所示。
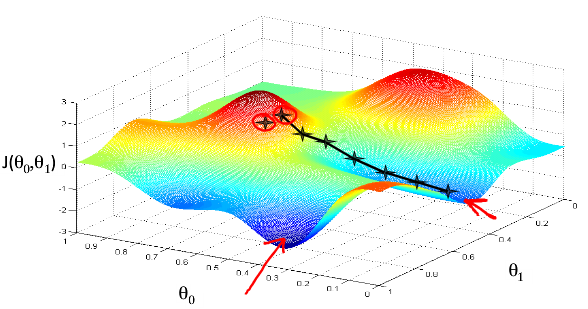
梯度下降算法:(要同时更新θ的值)


:=是赋值的意思
α:学习速率,是一个大于0的数,α的取值很重要
α过小:收敛的太慢,需要多次迭代
α过大:可能越过最低点,甚至导致无法收敛

学习速率只需选定即可,不需要在运行梯度下降算法的时候进行动态改变,随着斜率越来越接近于0,代价函数的变化幅度会越来越小,直到收敛到局部极小值。
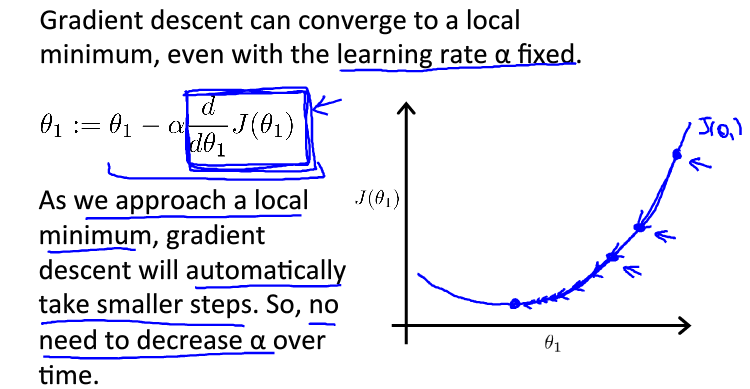
4、线性回归的梯度下降
只需要将代价函数带入梯度下降算法中即可。