L3-021 神坛(极角排序求三角形最小面积)

在古老的迈瑞城，巍然屹立着 n 块神石。长老们商议，选取 3 块神石围成一个神坛。因为神坛的能量强度与它的面积成反比，因此神坛的面积越小越好。特殊地，如果有两块神石坐标相同，或者三块神石共线，神坛的面积为 0.000。

长老们发现这个问题没有那么简单，于是委托你编程解决这个难题。

输入格式：

输入在第一行给出一个正整数 n（3 ≤n≤5000）。随后 n 行，每行有两个整数，分别表示神石的横坐标、纵坐标（-10⁹≤横坐标、纵坐标<10⁹）。

输出格式：

在一行中输出神坛的最小面积，四舍五入保留 3 位小数。

输入样例：

8
3 4
2 4
1 1
4 1
0 3
3 0
1 3
4 2

输出样例：

0.500

样例解释

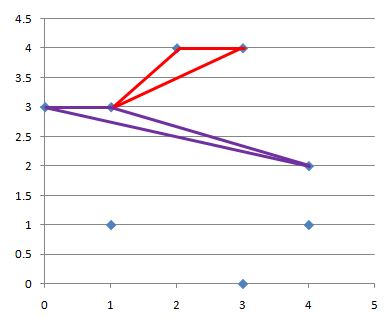
输出的数值等于图中红色或紫色框线的三角形的面积。

题意

N个点求最小三角形。

题解

首先需要知道3个点如何求S，0.5*abs(aXb)。

枚举每个点，极角排序，求出相邻向量的面积取个最小。

通过画图，可以发现若不取相邻，虽然也可以但是得多一层循环不能接受。

取相邻，可以发现刚好覆盖了所有最小的三角形。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=5005;

int n;
struct point//存储点
{
    ll x,y;
}p[N],c[N];
bool cmp(point a,point b)//按顺时针排序
{
    return b.y*a.x>b.x*a.y;
}
int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        scanf("%lld%lld",&p[i].x,&p[i].y);
    ll ans=1e18;
    for(int i=0;i<n;i++)
    {
        int k=0;
        for(int j=0;j<n;j++)
        {
            if(i!=j)
            {
                c[k].x=p[j].x-p[i].x;
                c[k].y=p[j].y-p[i].y;
                k++;
            }
        }
        sort(c,c+k,cmp);
        for(int j=1;j<k;j++)
            ans=min(ans,abs(c[j].y*c[j-1].x-c[j].x*c[j-1].y));
    }
    printf("%.3f
",ans/2.);
    return 0;
}