R语言代写使用Profviz进行Metropolis-in-Gibbs抽样和运行时间分析

对于许多模型，如物流模型，没有共轭先验 - 所以Gibbs不适用。正如我们在第一篇文章中看到的那样，蛮力网格方法太慢而无法扩展到真实环境。

这篇文章展示了我们如何使用Metropolis-Hastings（MH）从每个被阻挡的Gibbs迭代中的非共轭条件后验中进行采样 - 这是一种比网格方法更好的替代方案。

 模型

该示例的模拟数据是​患者的横截面数据集。有一个二元结果，​一个二元治疗变量​，和一个混淆年龄。年龄是一个分类变量，有3个级别。我使用2个假人控制它（一个类别作为参考）。我用贝叶斯逻辑回归建模：

​

​

以上，​假设已知。注意我​用来表示1000×4模型矩阵并​表示4×1参数向量。我还在​已知的超参数之前放置了反伽马。对于Metropolis-in-Gibbs来说，这是一个相当现实的激励示例：

1. 我们有一个二元结果，我们使用非线性链接函数。
2. 我们需要调整一个混淆器。
3. 我们正在估算更多我们关心的参数。在这种情况下，我们真正关心治疗效果的估计​，因此其他系数在某种意义上是讨厌的参数。我不会说这是一个“高维”设置，但它肯定会让采样器紧张。

非标准化的后验条件 

让我们来看看这个模型的（非标准化的）条件后验。我不会进行推导，但它遵循我以前的帖子中使用的相同程序。
​
回想一下，我们正在建模​。这里​表示​模型矩阵的行​，并​指示患者。

这里没有共轭！这种条件分布不是已知的分布，因此我们不能简单地使用Gibbs从中进行采样。相反，在每个gibbs迭代中，我们需要另一个采样步骤来从这个条件后验中抽取。第二个采样器将是MH采样器。如果您需要更新Gibbs，请参阅上面链接的上一篇文章。

旁注：条件后验​ 是共轭的。因此，在每个Gibbs迭代中，我们可以使用标准函数从反伽马中进行采样。这里不需要第二个采样步骤。唷！

MH采样

目标是从中抽样​。请注意，这是一个四维密度。为了简化说明，假设我们只有一个​，并且它的条件密度是单峰的。MH采样器的工作原理如下：

1. 制定一个初步的“提案”，​以便开始采样。
2. 从围绕中心的分布画出​。这称为提案分布，在标准情况下，必须是对称的  ​。我们可以用一个​。现在让我们假设我们将提案分布的方差设置为某个常数。
3. 现在我们从提案分发中抽取新的数据​。然后，我们计算在上一次抽奖中评估的非标准化密度​与当前建议的比率​：   ​
4. 如果该比率大于1，则当前建议的密度高于先前值的密度。所以我们“接受”提案并设定​。然后，我们使用以中心为中心的提案分发重复步骤2-4  ​，然后生成新提案。如果该比率小于1，则当前建议值的密度低于先前的提议。在这种情况下，我们接受​概率​。

因此，总是接受产生更高条件后验评估的提议。然而，有时只接受密度评估较低的建议 - 提案的相对密度评估越低，其接受概率越低（直观！）。经过多次迭代，接受来自后部高密度区域的抽取，并且接受的建议序列“爬上”到高密度区域。一旦序列到达这个高密度区域，它往往会留在那里。因此，在许多方面，您可以将MH视为随机“爬山”算法。 

 ​我们有一个协方差矩阵，而不是标量方差参数。因此，我们的提议是系数的向量。在这个意义上，我们运行一个被阻挡的Gibbs - 使用MH在每次迭代中绘制整个系数块。

• 跳跃分布的方差是一个重要参数。如果方差太小，当前的提议可能会非常接近最后一个值，因此​将接近1.因此我们会非常频繁地接受，但因为接受的值彼此如此接近，我们会爬到高位在许多迭代中缓慢地密度区域。如果方差太高，一旦到达那里，序列可能无法保留在高密度区域中。文献表明，在高维度（超过5个参数）中，最佳接受率约为24％。
• 许多“自适应”MH方法是这里描述的基本算法的变体，但包括调谐周期以找到产生最佳接受率的跳跃分布方差。
• MH中计算密集度最高的部分是密度评估。对于每个Gibbs迭代，我们必须两次评估4维密度：一次在当前提案中，一次在先前接受的提议中。
• 虽然符号很容易扩展到高维度，但性能本身在更高的维度上会恶化。原因很简单，但非常有趣。Michael Betancourt的这篇论文  解释了Gibbs和MH在更高维度上的不足，并概述了哈密尔顿蒙特卡罗（HMC）如何克服这些困难。据我所知：在更高的尺寸，密度不等于体积。由于进入高容量区域确实是我们想要的，并且由于标准MH到达高密度区域，因此MH在高维度上无法有效地探索高容量区域。在低尺寸，密度很接近体积，所以这不是一个问题。

结果

​

还有一些改进的余地：

• 接受率仅为18％，我可以调整跳跃分布协方差矩阵以获得更优的速率。
• 我认为更多的迭代肯定会有所帮助。这些链看起来还不错，但仍然相当自相关。

关于贝叶斯范式的好处是所有推理都是使用后验分布完成的。系数估计现在是对数尺度，但如果我们想要优势比，我们只是对后抽取进行取幂。如果我们想要比值比的区间估计，那么我们可以抓住指数后抽取的2.5和97.5百分位数。就这么简单 - 没有delta-method垃圾。

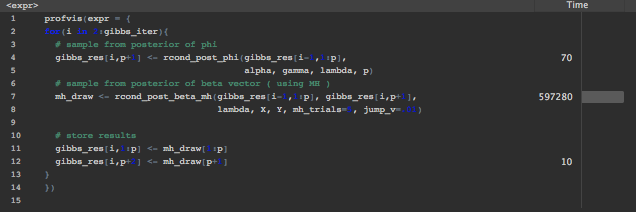
之前我曾提到MH是昂贵的，因为每次Gibbs迭代必须对log后验进行两次评估。下面是使用R包profviz进行的配置文件分析。for循环运行Gibbs迭代。在每个Gibbs迭代中，我调用函数rcond_post_beta_mh（），它使用MH从参数向量的条件后验产生绘制。请注意，它占用了大部分运行时。

​

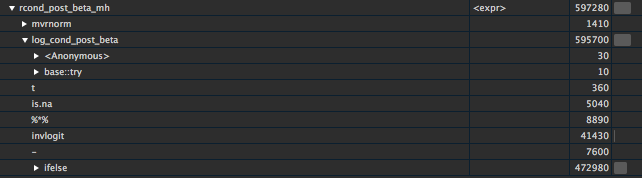
潜入rcond_post_beta_mh（），我们看到子程序log_cond_post_beta（）是MH运行的瓶颈。该函数是β向量的对数条件后验密度，其被评估两次。

​

如果您有任何疑问，请在下面发表评论。