原文链接:http://tecdat.cn/?p=6335
2014年9月18日,苏格兰居民将投票进行公民投票决定是否独立于英国。虽然运动之前已经保持了相当健康的领先优势,但是根据投票意向的民意调查,竞选已经大大收紧。特别是,两个民意调查现在已经显示出更大的比例,表示他们将投票赞成投票比例。由于上周进行了一系列民意调查,结果略有不同,我决定对其进行简单的Meta分析。根据现有证据,调查结果,估计当前的状态。
数据
包括从9月14日进行的最后六个投票,网站给出的数据whatscotlandthinks.org。如下所示。
| 民意调查开始 | 民意调查结束 | #选民 | #yes |
|---|---|---|---|
| 2014年9月9日 | 2014年11月9日 | 1205 | 571 |
| 2014年9月9日 | 2014年11月9日 | 820 | 400 |
| 2014年9月9日 | 2014年11月9日 | 992 | 475 |
| 2014年10月9日 | 2014年12月9日 | 844 | 389 |
| 2014年10月9日 | 2014年12月9日 | 642 | 345 |
| 2014年10月9日 | 14/09/2014 | 943 | 466 |
分析
用R进行分析。此函数结合了和被调查数字(不包括未定数)的数量,以给出对选民的平均比例的总体估计。进行两项分析,一项是所谓的固定效应分析,第二项是随机效应分析。
结果
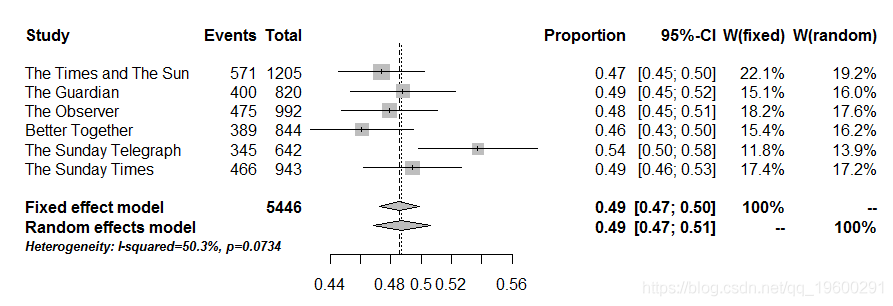
下面所谓的森林图显示了分析的结果。投票的总体估计比例为(在随机效应模型下)为48.72%,95%置信区间为46.82%至50.62%。因此,仅基于这六个民意调查(并参见下面的警告),估计投票比例是低于50%,而置信区间显示数据与“真实”比例一致,高于50 %。
来自不同研究的95%置信区间与每个基本上重叠,说明了在每个研究中给出(相对)小数量的点,结果的微小差异可能纯粹是由于抽样误差。
这里提出的简单分析可能存在许多缺陷。
荟萃分析就好像随机抽样一样。事实上,民意调查样本是使用更复杂的调查设计技术构建的,并且可能不应该像我所做的那样进行分析(就像它们是简单的随机样本一样)。
R输出
对于那些感兴趣的人,如下所示是分析的R输出,给出每个民意调查的比例,每个民意调查的95%CI,分配给每个民意调查的权重(在固定和随机效应分析中),估计I ^ 2(可归因于真实异质性的变异比例)。