原文链接：http://tecdat.cn/?p=6432
危险率函数
让我们模拟R中的一些数据：
n < - 10000
h < - 0.5
t < - -log（runif（n））/ h
该代码模拟了危险函数的存活时间，即常数。
事件< - 1 *（t <5）
时间< - t
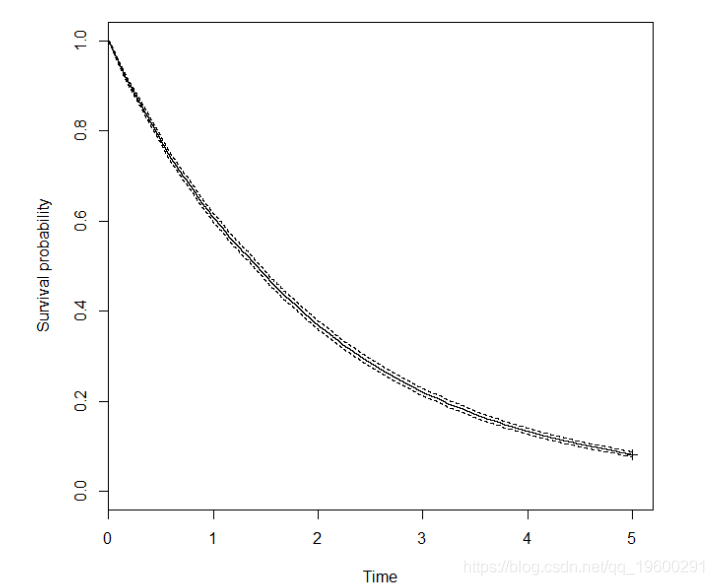
obstime [obstime> = 5] < - 5现在让我们使用R中的生存包绘制估计的生存函数：
survfit < - survfit（Surv（obstime，event）~1） 
Kaplan-Meier
95％置信区间限制非常接近此处的估计线，因为我们已经模拟了具有大样本量的数据集。
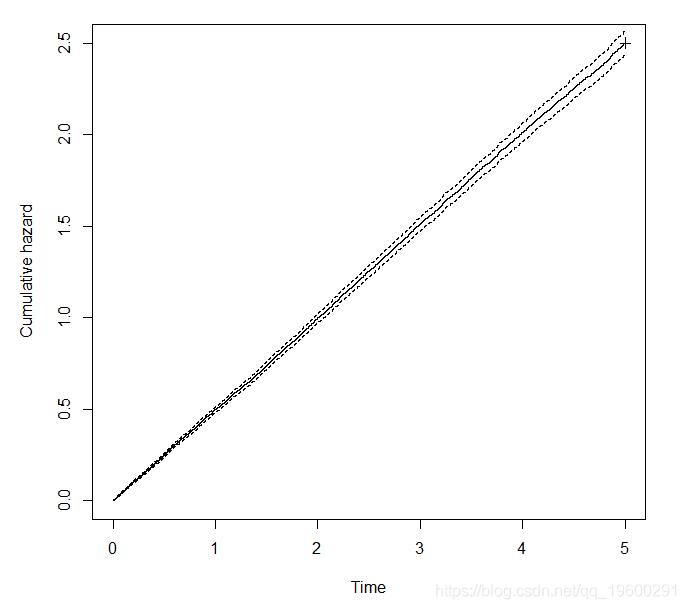
累积危险率函数
为了确定危险函数是否在变化，我们可以绘制累积危险函数，
plot（survfit，fun =“cumhaz”）
危险变化
有时危险函数不会是恒定的，这将导致累积危险函数的梯度/斜率随时间变化。
我们现在将再次模拟生存时间 ：
highrisk < - 1 *（runif（n）<0.5）
h < - 0.5 + highrisk * 1.5
t < - -log（runif（n））/ h
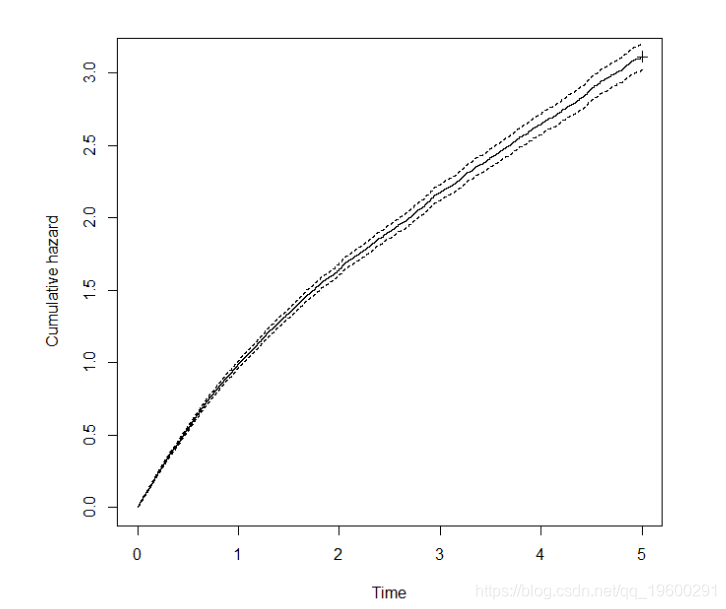
obstime [obstime> = 5] < - 5我们再次绘制累积危险函数：
累积危险图，其中样本由50％低风险和50％高风险对象组成
该图的自然解释是受试者经历的危险随着时间的推移而减少，因为累积危险函数的梯度/斜率随时间降低。
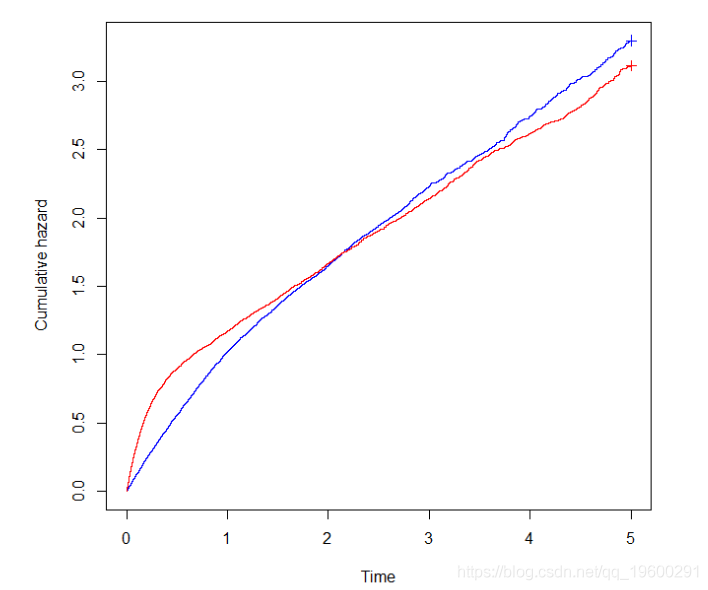
改变风险比
在我们比较两组生存率的研究中可能出现同样的问题，例如在比较两种治疗方案的随机试验中。这种比较通常通过估算两组之间的风险比来概括，假设两组的危害比率随着时间的推移是恒定的，使用Cox的比例风险模型。
highrisk < - 1 *（runif（n）<0.5）
治疗< - 1 *（runif（n）<0.5）
t < - -log（runif（n））/ h
事件< - 1 *（t <5）
时间< - t
obstime [obstime> = 5] < - 5现在让我们分别按治疗组绘制累积危险函数：
