原文链接:http://tecdat.cn/?p=24067
原文出处:拓端数据部落公众号
此示例基于电视节目的在线收视率。我们将从抓取数据开始。
-
-
# 加载软件包。
-
packages <- c("gplot2", "MASS", "reshpe", "splnes",
-
"XML")
-
分析的系列是亚伦·索尔金 (Aaron Sorkin) 的 《白宫风云》。
-
-
if (!fle.eiss(fie)) {
-
# 解析HTML内容。
-
html <- htmlPrse(lis?si=17ectn=a")
-
# 根据id选择表格。
-
tml <- pahppl(html, //tal[@d='Tle']"[1] ?
-
# 转换为数据集。
-
da <- reHTML(hml)
-
# 第一个数据行。
-
head(da )
-
# 保存本地副本。
-
write.csv(ata[, -3], fle)
-
-
# 读取本地副本
-
daa <- red.sv(fie)
-
# 检查结果
-
str(dat)
-

Mean 是每集的平均评分,所以我们有一个参数, Count 是每集的投票数,所以我们有一个样本大小。使用标准误差方程![]() ,我们将计算每个评分的“误差幅度”。请注意,由于有几集收视率非常高,因此收视率分布不正常。
,我们将计算每个评分的“误差幅度”。请注意,由于有几集收视率非常高,因此收视率分布不正常。
-
-
# 计算季
-
daa$saon <- 1 + (daX - 1)%/%22
-
# 特殊情况
-
at$sasn[which(dta$sesn > 7)] <- c(7, NA)
-
# 因子变量
-
daa$saon <- fator(aa$sesn)
-
我们对数据采取的最后一步是添加季编号,以便以后能够在绘图上区分它们。 除了两个特例(最后一季有 23 集,一个节目是电影特辑)外,《白宫风云》每一季 都有 22 集。我们使用除以 22 的余数来计算季,修复特殊情况,并将变量分解为绘图目的。
-
-
# 计算季
-
asaon <- 1 + (aX - 1)%/%22
-
# 特殊情况
-
dtseson[wich(dtsasn > 7)] <- c(7, A)
-
# 因子变量
-
dtseson <- fctor(dasasn)
-
最后的图使用 95% 和 99% 的置信区间来可视化不确定性。
-
qlot(dta =dat, x = X, y = mu, clr =sasn, gem = "pont") +
-
genge(es(yin = u - 1.96*se, ymx = u + 1.96*se), alpa = .5) +
-
golie(as(yin =mu - 2.58*se, yax = mu + 2.58*e), apa = .5) +
-
-
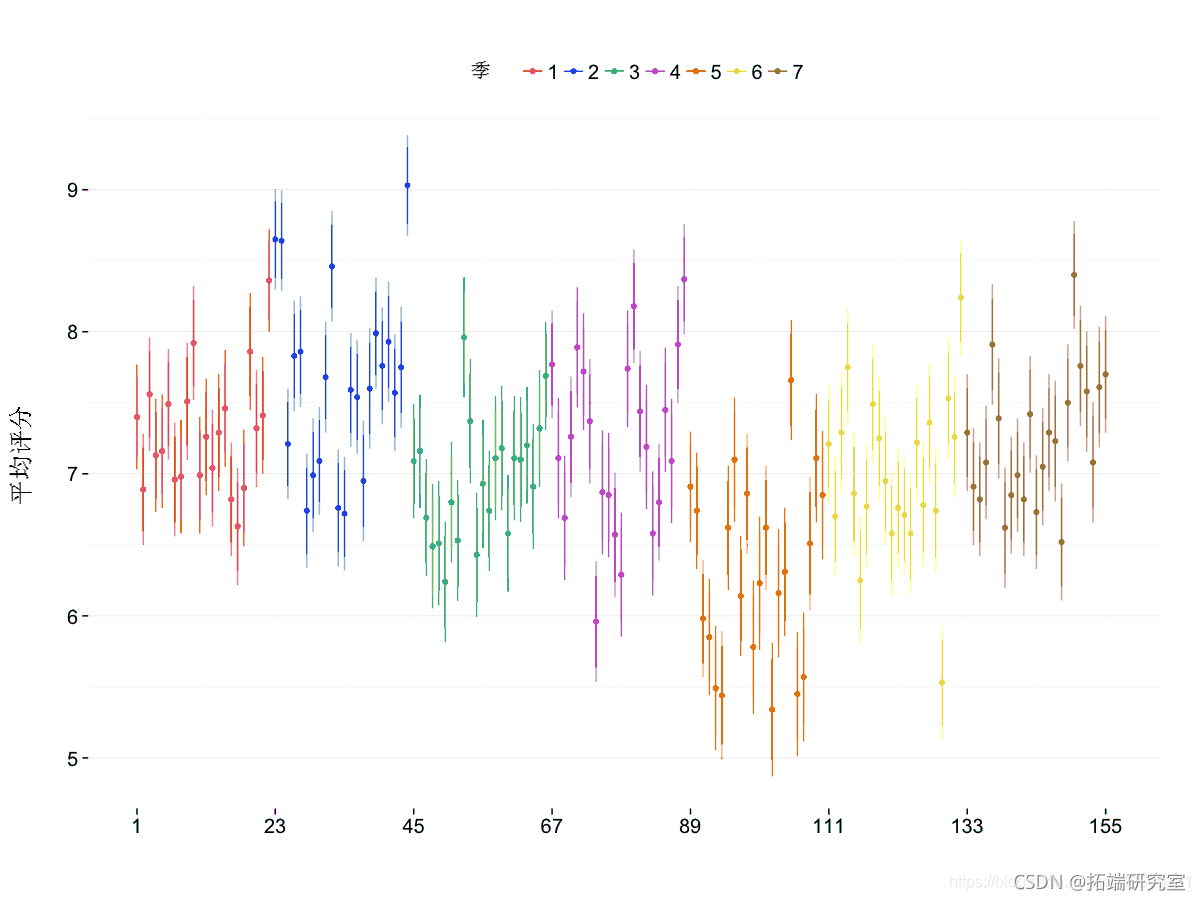
该图对于每个季节的平均收视率会更有用,这些收视率很容易用该ddply() 函数检索 。还计算了最小和最大集数,以便能够绘制每个季节的水平段。由于我们将之前的绘图保存为 ggplot2 对象,因此添加线条只需要对额外的图形元素进行编码并将其添加到保存的元素之上。
-
# 计算季平均值。
-
men <- dply(daa,.(easn), summrs,
-
ma = mean),
-
xmi= in(X,
-
xmx = ma(X)
-
# 将平均值添加到绘图中。
-
g + go_eme(daa = eas,
-
as( xmin, max, = mean, en= man))
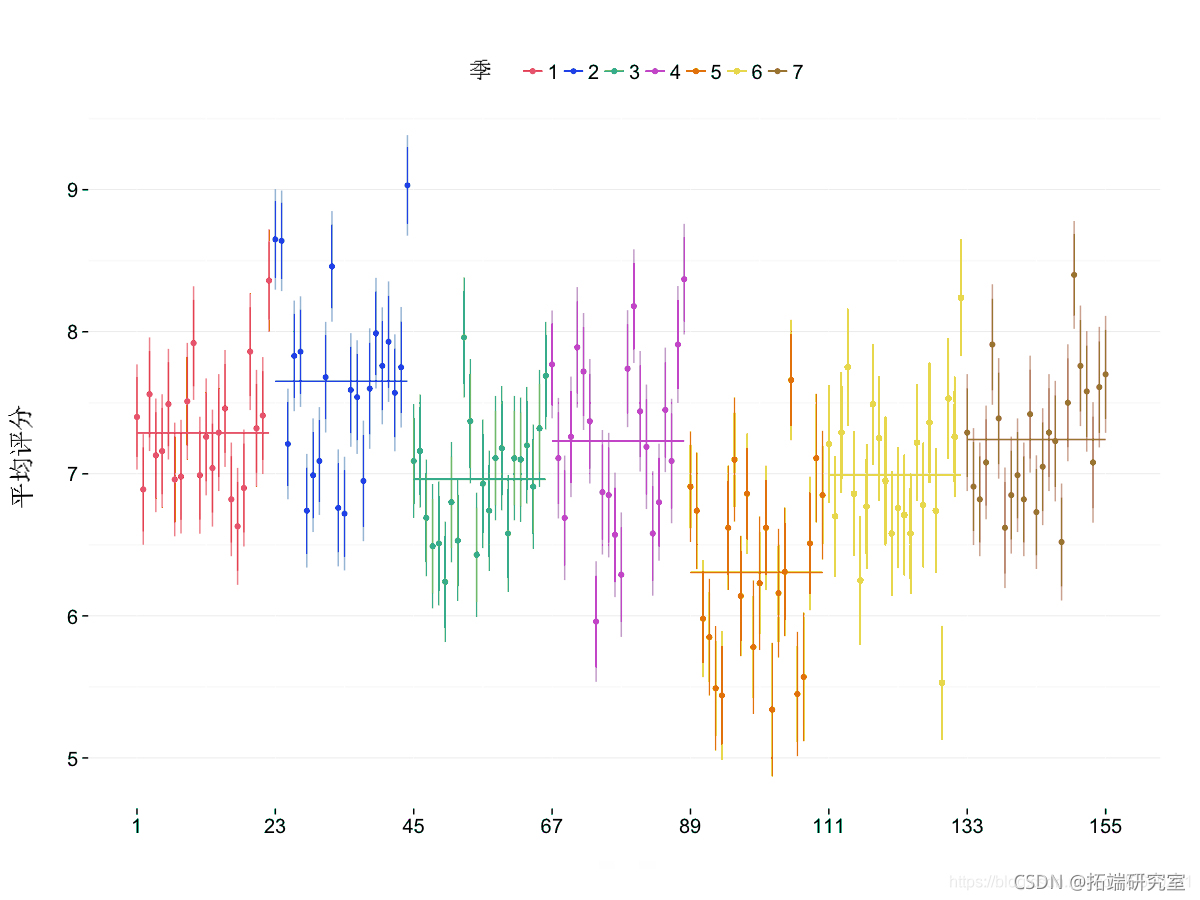
变化点检测算法
如果您的目标是找到系列中的突然变化,请使用变化点检测算法。
-
# PELT算法计算变化点。
-
p <- tmean(atamu, 'PELT')
-
# 提取结果。
-
xmin <- c(0, max[-legh(xmax)])
-
# 绘图。
-
gem_segnt(dat = eg)
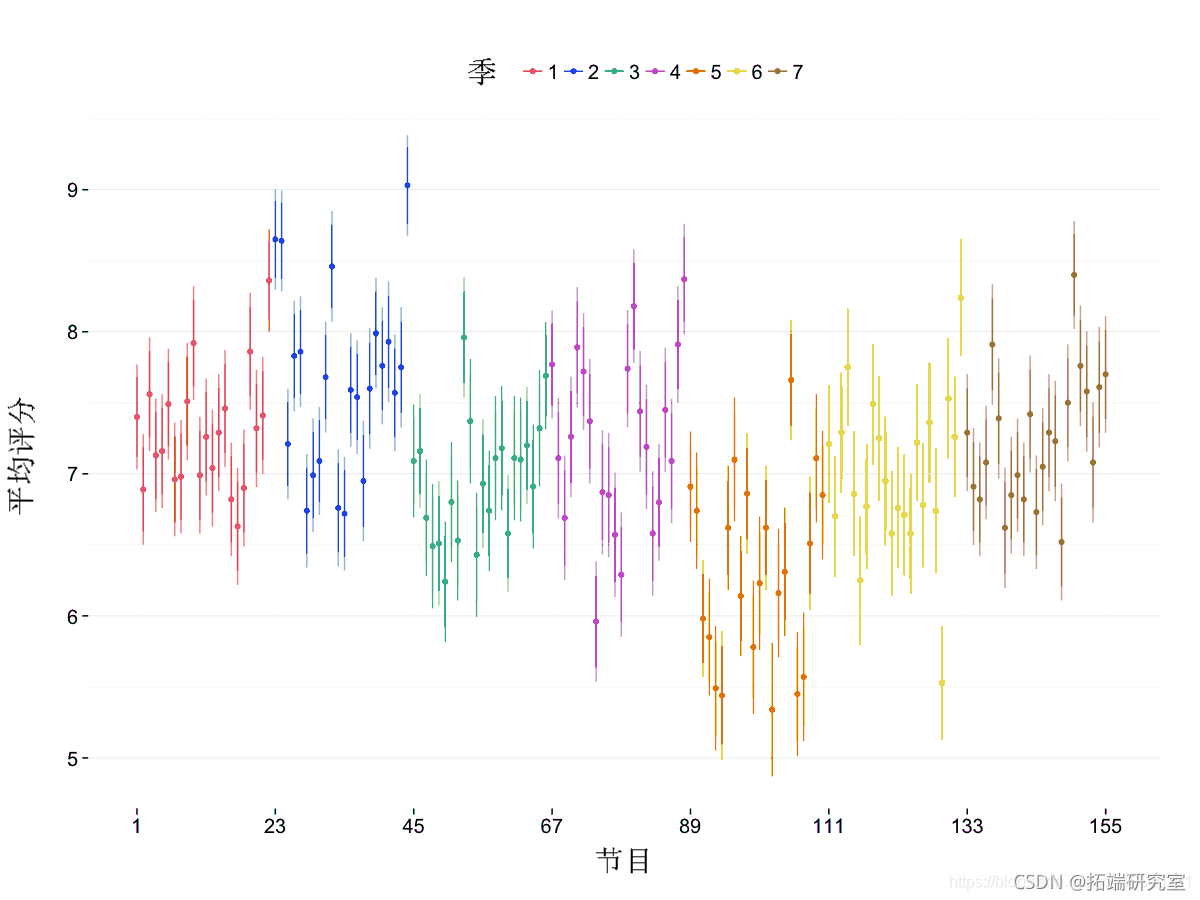
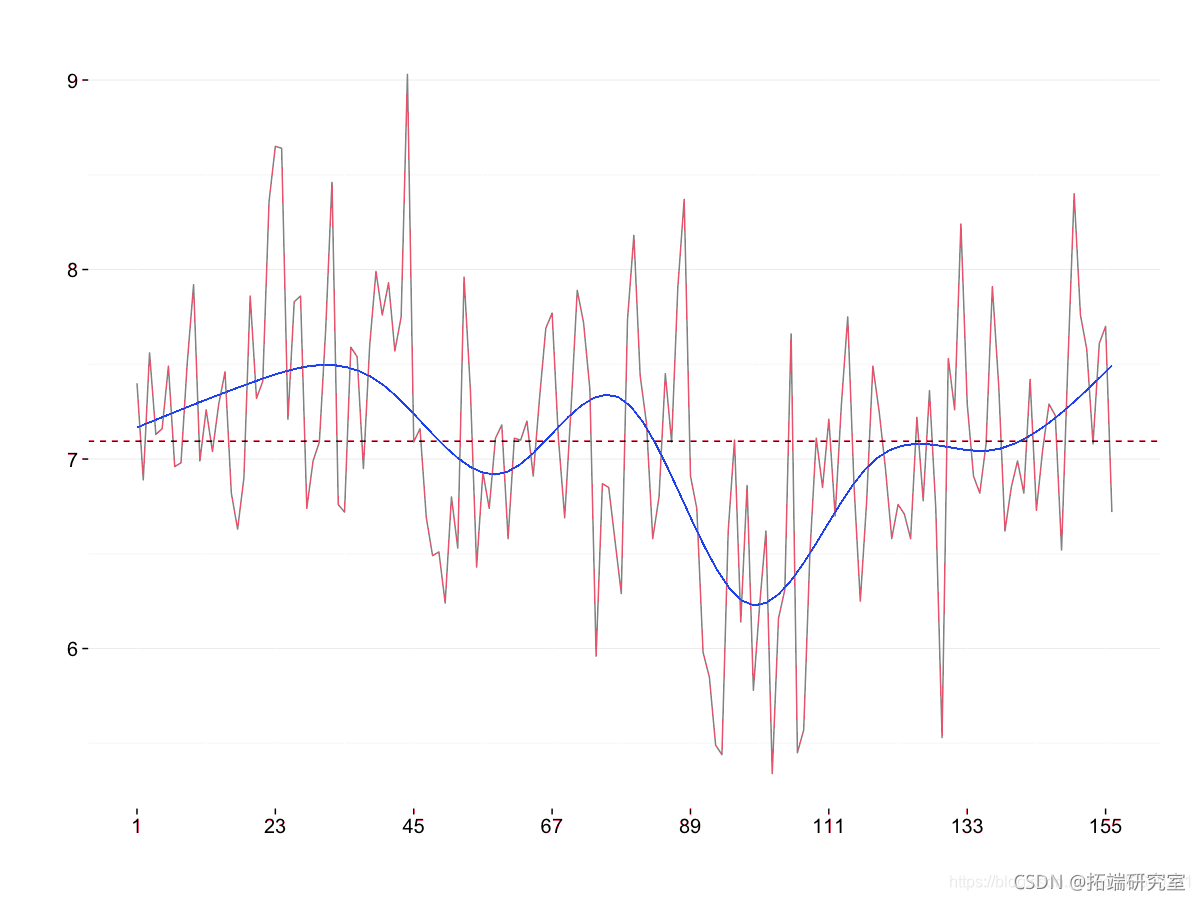
平滑算法:LOESS(局部加权回归)和三次样条
现在让我们平滑这个系列。基本图都将使用相同的数据,我们将在其上叠加一条通过不同方法计算的趋势线。
-
-
# 绘图
-
plot(data
-
x = X,
-
y = mu,
-
alpa = I0.5),
-
gom = line")
-
-
平滑数据的最简单方法是使用局部多项式,我们将其应用于每个季节的分数,然后应用于它们的去趋势值。更复杂的平滑方法使用 splines 。它仅用于最后一个图中。
-
-
# 每一季的LOESS平滑
-
-
LOESS(se = FALSE) +
-
goln(y = tmu,neyp= dhe"+
-
as(colo = sason)
-
-
-
-
# 对去趋势的数值进行LOESS平滑处理
-
smooth(se = FALSE) +
-
eoin(es =memu)), itype = ") +
-
-
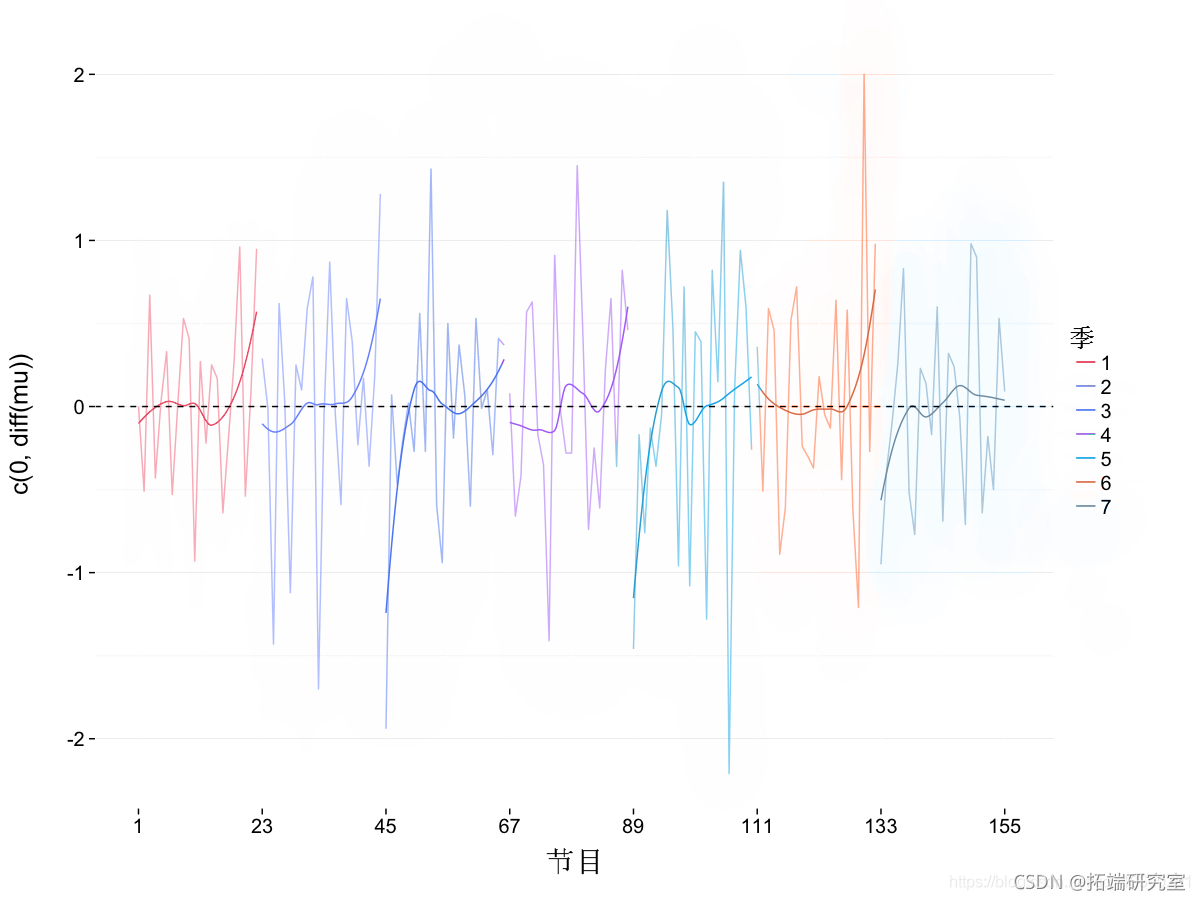
-
-
# 立方样条
-
g +
-
smooth( "m", ns(x, 8)
-
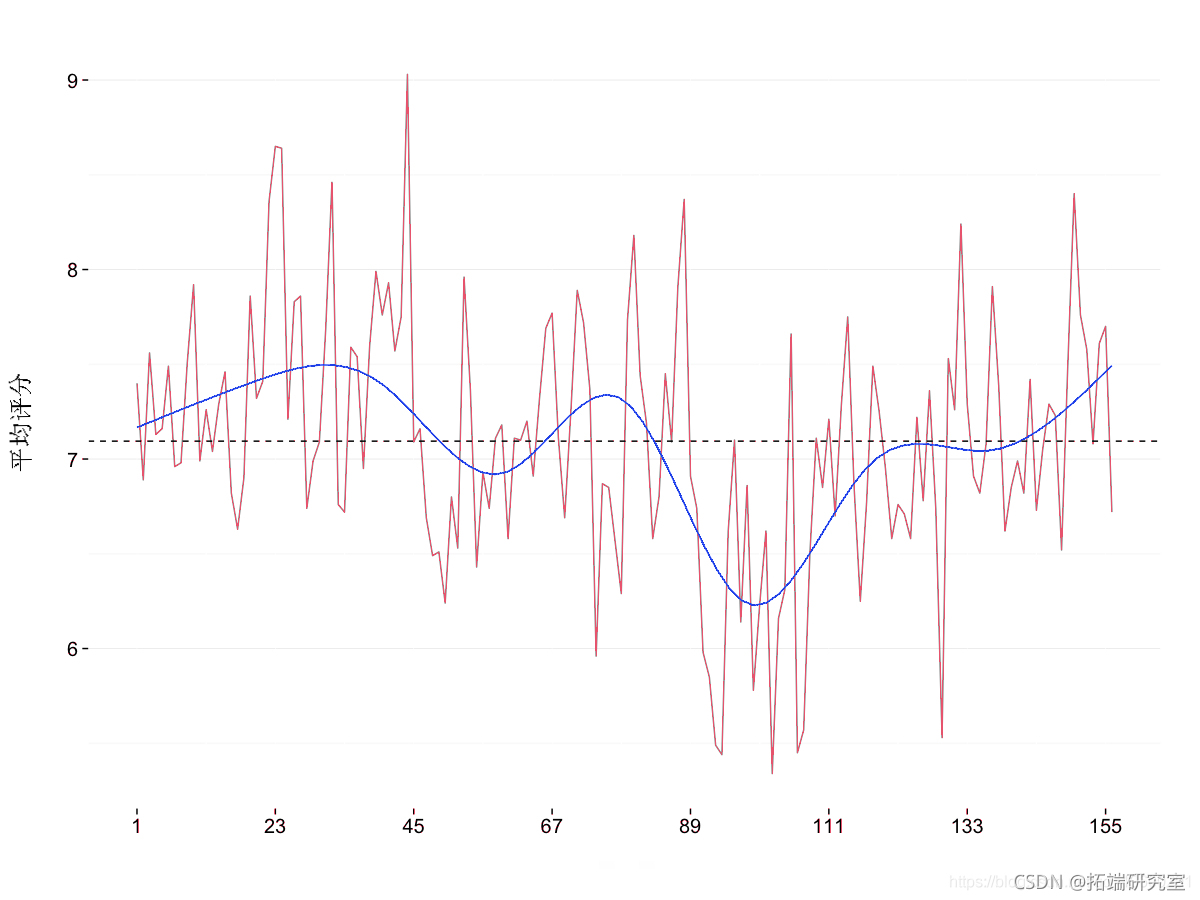
三次样条提供的信息与我们从变化点检测中了解到的情况几乎相同:该系列有三个时期,是由于观众收视率的一次下降。
-
-
# 三次样条和变化点
-
gmoth(method = ~ ns(x, 8))
-
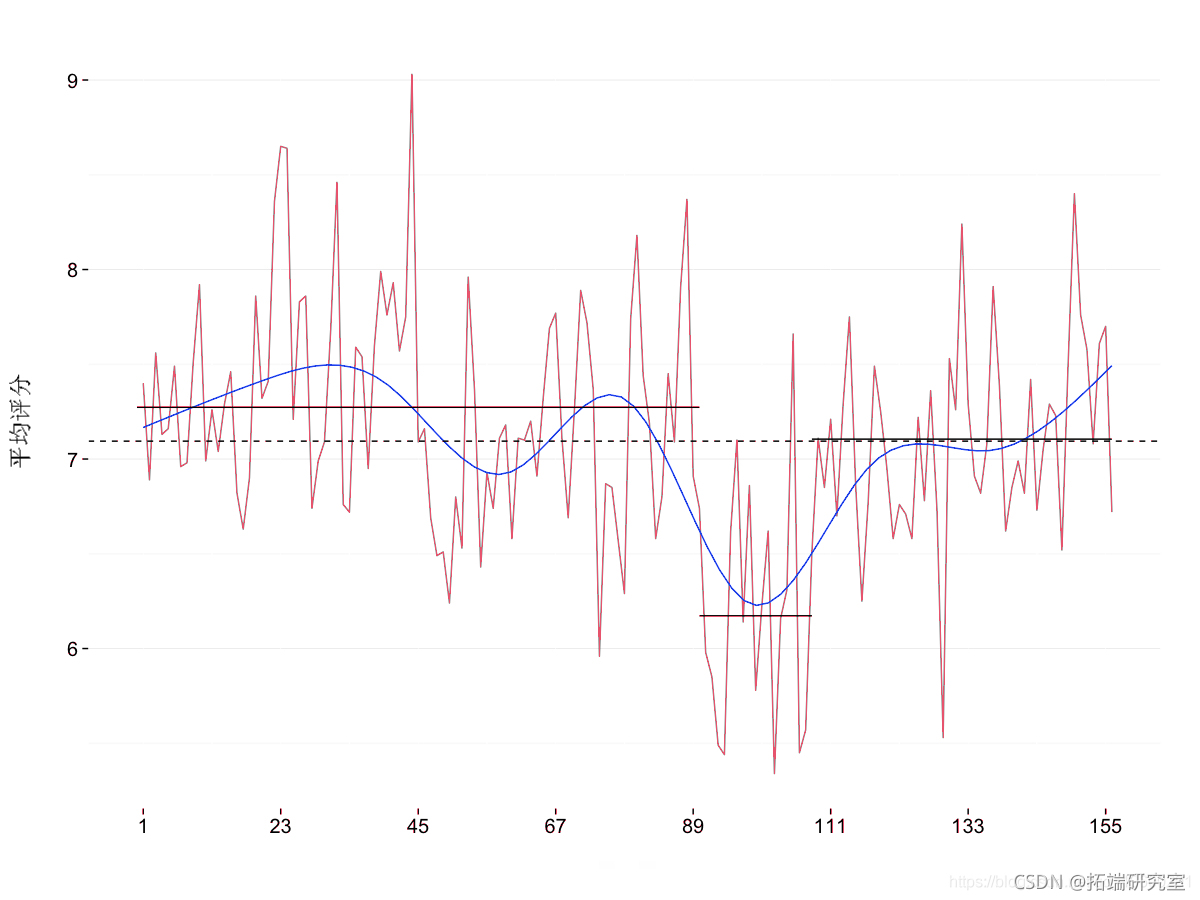

最受欢迎的见解
3.matlab中的偏最小二乘回归(PLSR)和主成分回归(PCR)
6.r语言中对LASSO回归,Ridge岭回归和Elastic Net模型实现