| Time Limit: 2000MS | Memory Limit: 10000K | |
| Total Submissions: 12265 | Accepted: 6484 |
Description
A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.
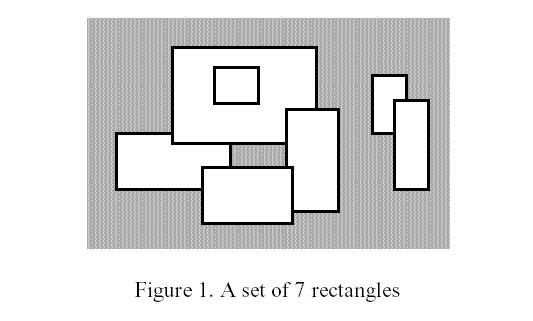
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.
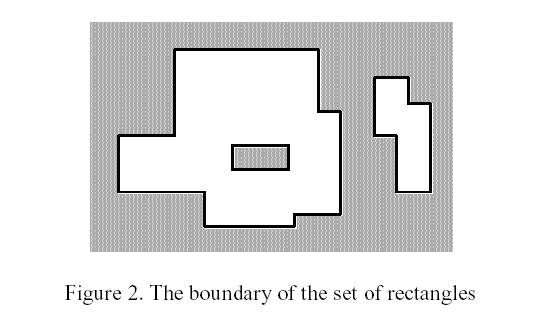
The corresponding boundary is the whole set of line segments drawn in Figure 2.
The vertices of all rectangles have integer coordinates.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

The vertices of all rectangles have integer coordinates.
Input
Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Output
Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.
Sample Input
7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16
Sample Output
228
Source
这题恶心,不想写题解
解释都在代码里了,自己看代码吧
#include <stdio.h> #include <algorithm> #define LEN 10000 using namespace std; struct Node { int left; int right; int count;//被覆盖次数 int line;//所包含的区间数量 int lbd;//左端点是否被覆盖 int rbd;//右端点是否被覆盖 int m;//测度,即覆盖的区间长度,如[2,8]就为6 }; struct ScanLine { int x;//横坐标 int y1;//扫描线的下端点 int y2;//扫描线的上端点 int flag;//若该扫描线属于矩形的左边的竖边, //如AB,则叫做入边,值为1,若属于矩形的右边的竖边,如CD,则叫做出边,值为0 }; struct Node node[LEN*4]; struct ScanLine scan[LEN]; int y[LEN]; void build(int l, int r, int i) { node[i].left = l; node[i].right = r; node[i].count = 0; node[i].m = 0; node[i].line = 0; if (r - l > 1) { int middle = (l + r)/2; build(l, middle, 2*i + 1); build(middle, r, 2*i + 2); } } //更新测度m void update_m(int i) { if (node[i].count > 0) node[i].m = y[node[i].right] - y[node[i].left]; else if (node[i].right - node[i].left == 1) node[i].m = 0; else { node[i].m = node[2*i + 1].m + node[2*i + 2].m; } } //更新line void update_line(int i) { if (node[i].count > 0) { node[i].lbd = 1; node[i].rbd = 1; node[i].line = 1; } else if (node[i].right - node[i].left == 1) { node[i].lbd = 0; node[i].rbd = 0; node[i].line = 0; } else { node[i].lbd = node[2*i + 1].lbd; node[i].rbd = node[2*i + 2].rbd; node[i].line = node[2*i + 1].line + node[2*i + 2].line - node[2*i + 1].rbd*node[2*i + 2].lbd; } } void insert(int l, int r, int i)//l和r分别是这条扫描线的下端点和上端点的纵坐标 //相当于区间修改 { //在这里要取离散化之前的原值进行比较 if (y[node[i].left] >= l && y[node[i].right] <= r) //如果这个区间内最下的点的纵坐标大于insert扫描线的上端点的纵坐标 //且这个区间内最上的点的纵坐标小于insert扫描线的下端点的纵坐标 (node[i].count)++;//这个区间包含于这条线段,一定覆盖了这个区间内的扫描线 else if (node[i].right - node[i].left == 1)return;//因为坐标都是整数 else { int middle = (node[i].left + node[i].right)/2; if (r <= y[middle])//这条扫描线完全包含于这个区间的中点到最下 insert(l, r, 2*i + 1); else if (l >= y[middle])//完全包含于这个区间的最上到中点 insert(l, r, 2*i + 2); else//穿过中点 { insert(l, y[middle], 2*i + 1); insert(y[middle], r, 2*i + 2); } } update_m(i); update_line(i); } void remove(int l, int r, int i) { //在这里要取离散化之前的原值进行比较 if (y[node[i].left] >= l && y[node[i].right] <= r) (node[i].count)--;//完全被包含就删去这条边 else if (node[i].right - node[i].left == 1) return; else { int middle = (node[i].left + node[i].right)/2; if (r <= y[middle]) remove(l, r, 2*i + 1); else if (l >= y[middle]) remove(l, r, 2*i + 2); else { remove(l, y[middle], 2*i + 1); remove(y[middle], r, 2*i + 2); } } update_m(i); update_line(i); } bool cmp(struct ScanLine line1, struct ScanLine line2) { if (line1.x == line2.x) return line1.flag > line2.flag; return (line1.x < line2.x); } int main() { int n; scanf("%d", &n);//输入有几个矩形 int x1, y1, x2, y2; int i = 0; while (n--) { scanf("%d %d %d %d", &x1, &y1, &x2, &y2);//(x1,y1)左下,(x2,y2)右上 scan[i].x = x1;//加扫描线 scan[i].y1 = y1; scan[i].y2 = y2; scan[i].flag = 1; y[i++] = y1;//y[]记录所有点的纵坐标 scan[i].x = x2; scan[i].y1 = y1; scan[i].y2 = y2; scan[i].flag = 0; y[i++] = y2; } sort(y, y + i);//所有纵坐标从下到上排序 sort(scan, scan + i, cmp);//所有扫描线从左到右排序 int unique_count = unique(y, y + i) - y;//y数组中不重复的个数 build(0, unique_count - 1, 0);//离散化,建立线段树 int perimeter = 0; int now_m = 0; int now_line = 0; for (int j = 0; j < i; j++)//枚举每条扫描线 { if (scan[j].flag)//如果是左边 insert(scan[j].y1, scan[j].y2, 0); else//如果是右边 remove(scan[j].y1, scan[j].y2, 0); if (j >= 1) perimeter += 2*now_line*(scan[j].x - scan[j-1].x); perimeter += abs(node[0].m - now_m); now_m = node[0].m; now_line = node[0].line; } printf("%d ", perimeter); return 0; }