best AVL tree visualization
http://www.cs.umd.edu/class/spring2002/cmsc420-0401/demo/avltree/
尼码:这个太强大了:
http://www.qmatica.com/DataStructures/Trees/AVL/AVLTree.html
http://en.wikipedia.org/wiki/AVL_tree
AVL tree
| AVL tree | ||
|---|---|---|
| Type | Tree | |
| Invented | 1962 | |
| Invented by | G. M. Adelson-Velskii andE. M. Landis | |
| Time complexity in big O notation | ||
| Average | Worst case | |
| Space | O(n) | O(n) |
| Search | O(log n) | O(log n) |
| Insert | O(log n) | O(log n) |
| Delete | O(log n) | O(log n) |
In computer science, an AVL tree (Adelson-Velskii and Landis' tree, named after the inventors) is a self-balancing binary search tree, and it was the first such data structure to be invented.[1] In an AVL tree, theheights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take O(log n) time in both the average and worst cases, where n is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.
The AVL tree is named after its two Soviet inventors, G. M. Adelson-Velskii and E. M. Landis, who published it in their 1962 paper "An algorithm for the organization of information".[2]
AVL trees are often compared with red-black trees because both support the same set of operations and take O(logn) time for the basic operations. For lookup-intensive applications, AVL trees are faster than red-black trees because they are more rigidly balanced.[3] Similar to red-black trees, AVL trees are height-balanced, but in general not weight-balanced nor μ-balanced for any  ;[4] that is, sibling nodes can have hugely differing numbers of descendants.
;[4] that is, sibling nodes can have hugely differing numbers of descendants.
Contents
[hide]Operations[edit]
Basic operations of an AVL tree involve carrying out the same actions as would be carried out on an unbalanced binary search tree, but modifications are followed by zero or more operations called tree rotations, which help to restore the height balance of the subtrees.
Searching[edit]
Once a node has been found in a balanced tree, the next or previous nodes can be explored in amortizedconstant time. Some instances of exploring these "nearby" nodes require traversing up to 2×log(n) links (particularly when moving from the rightmost leaf of the root's left subtree to the leftmost leaf of the root's right subtree; in the example AVL tree, moving from node 14 to the next but one node 19 takes 4 steps). However, exploring all n nodes of the tree in this manner would use each link exactly twice: one traversal to enter the subtree rooted at that node, another to leave that node's subtree after having explored it. And since there are n−1 links in any tree, the amortized cost is found to be 2×(n−1)/n, or approximately 2.(中根遍历,每个边访问两次)
Insertion[edit]
After inserting a node, it is necessary to check each of the node's ancestors for consistency with the rules of AVL. The balance factor is calculated as follows: balanceFactor = height(left-subtree) - height(right-subtree). For each node checked, if the balance factor remains −1, 0, or +1 then no rotations are necessary. However, if balance factor becomes less than -1 or greater than +1, the subtree rooted at this node is unbalanced. If insertions are performed serially, after each insertion, at most one of the following cases needs to be resolved to restore the entire tree to the rules of AVL.
Suppose inserting one element causes P's balance factor to go out of range. It must be that insertion caused the height of one of P's child nodes to increase by 1 (but not the other). Without loss of generality, assume that the height of L, P's left, was increased. The following procedure can restore balance at P:
if (balance_factor(L) > 0) {
// In the illustration to the right,
// this is the first step in the left-right case.
rotate_left(L);
}
// This brings us to the left-left case.
rotate_right(P);
The right-left and right-right cases are analogous. The names of the cases refer to the portion of the tree that is reduced in height.
In order to restore the balance factors of all nodes, first observe that all nodes requiring correction lie along the path used during the initial insertion. If the above procedure is applied to nodes along this path, starting from the bottom (i.e. the node furthest away from the root), then every node in the tree will again have a balance factor of -1, 0, or 1.(自下而上修正关键路径上每个结点)
Deletion[edit]
If the node is a leaf or has only one child, remove it.(叶结点或单孩子结点:直接删除,挂接子树)
Otherwise, replace it with either the largest in its left sub tree (in order predecessor) or the smallest in its right sub tree (in order successor), and remove that node. The node that was found as a replacement has at most one sub tree. After deletion, retrace the path back up the tree (parent of the replacement) to the root, adjusting the balance factors as needed.
(两个孩子的结点,用前驱结点或后继结点替换,归约为上面 叶结点或单孩子结点的删除)
As with all binary trees, a node's in-order successor is the left-most child of its right subtree, and a node's in-order predecessor is the right-most child of its left subtree. In either case, this node will have zero or one children. Delete it according to one of the two simpler cases above.
In addition to the balancing described above for insertions, if the balance factor for the tree is 2 and that of the left subtree is 0, a right rotation must be performed on P. The mirror of this case is also necessary.
case 1:原来高度相等,一个子树高度少1,总高度不变,自身平衡,不向上传播
The retracing can stop if the balance factor becomes −1 or +1 indicating that the height of that subtree has remained unchanged.(左子树或右子树少了一个结点,因子变成-1或1,原来是0,总高度不变)
case 2:原来高度不等,高度大的少了1,总高度少1,自身平衡,向上传播
If the balance factor becomes 0 then the height of the subtree has decreased by one and the retracing needs to continue(原来是1或者-1变成0,即一个子树比另一个高度多1,减少一个结点使两个高度相等,但总高度少1).
case 3:原来高度不等,高度少的少了1,总高度不变,自身调整,向上传播
If the balance factor becomes −2 or +2 then the subtree is unbalanced and needs to be rotated to fix it(高度小的减少一个).
If the rotation leaves the subtree's balance factor at 0 then the retracing towards the root must continue since the height of this subtree has decreased by one. This is in contrast to an insertion where a rotation resulting in a balance factor of 0 indicated that the subtree's height has remained unchanged.
The time required is O(log n) for lookup, plus a maximum of O(log n) rotations on the way back to the root, so the operation can be completed in O(logn) time.
Comparison to other structures[edit]
Both AVL trees and red-black trees are self-balancing binary search trees, so they are very similar mathematically. The operations to balance the trees are different, but both occur on the average in O(1) with maximum in O(log n). The real difference between the two is the limiting height. For a tree of size  :
:
- An AVL tree's height is strictly less than:[5][6]

- where
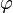 is the golden ratio.
is the golden ratio.
- A red-black tree's height is at most
 [7]
[7]
AVL trees are more rigidly balanced than red-black trees, leading to slower insertion and removal but faster retrieval.(检索快,插入删除慢)



