庆祝通过noip2018初赛,系列五题EP3.
题目背景
在人类智慧的山巅,有着一台字长为10485761048576位(此数字与解题无关)的超级计算机,著名理论计算机科
学家P博士正用它进行各种研究。不幸的是,这天台风切断了电力系统,超级计算机
无法工作,而 P 博士明天就要交实验结果了,只好求助于学过OI的你. . . . . .
题目描述
P 博士将他的计算任务抽象为对一个整数的操作。
具体来说,有一个整数xx,一开始为00。
接下来有nn个操作,每个操作都是以下两种类型中的一种:
-
1 a b:将xx加上整数acdot 2^ba⋅2b,其中aa为一个整数,bb为一个非负整数 -
2 k:询问xx在用二进制表示时,位权为2^k2k的位的值(即这一位上的11代表 2^k2k)
保证在任何时候,xgeqslant 0x⩾0。
输入输出格式
输入格式:
输入的第一行包含四个正整数n,t_1,t_2,t_3n,t1,t2,t3,nn的含义见题目描述,t_1t1,t_2t2,t_3t3的具体含义见子任务。
接下来nn行,每行给出一个操作,具体格式和含义见题目描述。
同一行输入的相邻两个元素之间,用恰好一个空格隔开。
输出格式:
对于每个询问操作,输出一行,表示该询问的答案(00或11)。对于加法操作,没有任何输出。
输入输出样例
10 3 1 2 1 100 0 1 2333 0 1 -233 0 2 5 2 7 2 15 1 5 15 2 15 1 -1 12 2 15
0 1 0 1 0
说明
在所有测试点中,1leqslant t_1 leqslant 3, 1 leqslant t_2 leqslant 4, 1 leqslant t_3 leqslant 21⩽t1⩽3,1⩽t2⩽4,1⩽t3⩽2。不同的 t_1, t_2, t_3t1,t2,t3 对应的特殊限制如下:
-
对于 t_1 = 1t1=1 的测试点,满足 a = 1a=1
-
对于 t_1 = 2t1=2 的测试点,满足 |a| = 1∣a∣=1
-
对于 t_1 = 3t1=3 的测试点,满足 |a| leqslant 10^9∣a∣⩽109
-
对于 t_2 = 1t2=1 的测试点,满足 0 leqslant b, k leqslant 300⩽b,k⩽30
-
对于 t_2 = 2t2=2 的测试点,满足 0 leqslant b, k leqslant 1000⩽b,k⩽100
-
对于 t_2 = 3t2=3 的测试点,满足 0 leqslant b, k leqslant n0⩽b,k⩽n
-
对于 t_2 = 4t2=4 的测试点,满足 0 leqslant b, k leqslant 30n0⩽b,k⩽30n
-
对于 t_3 = 1t3=1 的测试点,保证所有询问操作都在所有修改操作之后
-
对于 t_3 = 2t3=2 的测试点,不保证询问操作和修改操作的先后顺序
本题共 25 个测试点,每个测试点 4 分。各个测试点的数据范围如下:
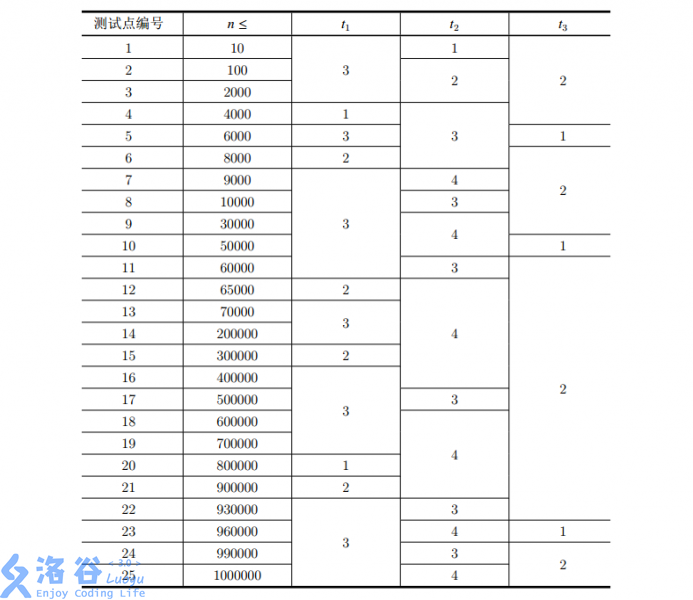
解题思路:
我们可以把二进制整数每30位压在一个int里面,然后进行加的操作时就是找到连续1后面的第一个0,再区间把1改成0,把第一个0改成1,
可以用区间or和区间and找出0,1的位置,并且可用线段树维护
(庆祝通过noip2018第三题)
下面上代码:
1#include<bits/stdc++.h>
2#define N 1000005
3using namespace std;
4const int inf=(1<<30)-1;
5const int m=1000000;
6struct node{
7 int And,Or,lazy,val;
8}tree[N*4];
9int n,t,a,b,res,op,x,pos,loc;
10void read(){
11 cin >> n >> t >> t >> t;
12 for (int i=0;i<=4000000;i++)
13 tree[i].lazy=-1;
14}
15void Add(int p,int l,int r,int v){
16 tree[p].And=v;
17 tree[p].Or=v;
18 tree[p].lazy=v;
19}
20void pushdown(int p,int l,int r,int mid){
21 if (tree[p].lazy==-1) return;
22 Add(p<<1,l,mid,tree[p].lazy);
23 Add(p<<1|1,mid+1,r,tree[p].lazy);
24 tree[p].lazy=-1;
25}
26int query_ans(int p,int l,int r,int x){
27 if (l==r) return tree[p].And;
28 int mid=l+r >> 1;
29 pushdown(p,l,r,mid);
30 int res=0;
31 if (x<=mid)
32 res=query_ans(p<<1,l,mid,x); else
33 res=query_ans(p<<1|1,mid+1,r,x);
34 return res;
35}
36int find0(int p,int l,int r,int x){
37 if (tree[p].And==inf) return -1;
38 if (l==r) return l;
39 int mid=l+r >> 1;
40 pushdown(p,l,r,mid);
41 int res=0;
42 if (x<=mid){
43 res=find0(p<<1,l,mid,x);
44 res=~res?res:find0(p<<1|1,mid+1,r,x);
45 } else
46 res=find0(p<<1|1,mid+1,r,x);
47 return res;
48}
49int find1(int p,int l,int r,int x){
50 if (tree[p].Or==0) return -1;
51 if (l==r) return l;
52 int mid=l+r >> 1;
53 pushdown(p,l,r,mid);
54 int res=0;
55 if (x<=mid){
56 res=find1(p<<1,l,mid,x);
57 res=~res?res:find1(p<<1|1,mid+1,r,x);
58 } else
59 res=find1(p<<1|1,mid+1,r,x);
60 return res;
61}
62void modify(int p,int l,int r,int x,int y,int v){
63 if (l>=x&&r<=y){
64 Add(p,l,r,v);
65 return;
66 }
67 int mid=l+r >> 1;
68 if (l>r||l>y||r<x) return;
69 pushdown(p,l,r,mid);
70 if (x<=mid) modify(p<<1,l,mid,x,y,v);
71 if (y>mid) modify(p<<1|1,mid+1,r,x,y,v);
72 tree[p].And=tree[p<<1].And&tree[p<<1|1].And;
73 tree[p].Or=tree[p<<1].Or|tree[p<<1|1].Or;
74}
75
76void inc(int num,int pos){
77 if (num==0) return;
78 res=query_ans(1,0,m,pos)+num;
79 if (res>inf){
80 modify(1,0,m,pos,pos,res-inf-1);
81 int p=find0(1,0,m,pos+1);
82 modify(1,0,m,pos+1,p-1,0);//区间改0
83 inc(1,p);
84 } else
85 modify(1,0,m,pos,pos,res);
86}
87void dec(int num,int pos){
88 if (num==0) return;
89 res=query_ans(1,0,m,pos)-num;
90 if (res<0){
91 modify(1,0,m,pos,pos,res+inf+1);
92 int p=find1(1,0,m,pos+1);
93 modify(1,0,m,pos+1,p-1,inf);
94 dec(1,p);
95 } else
96 modify(1,0,m,pos,pos,res);
97}
98void solve(){
99 for (int i=1;i<=n;i++){
100 scanf("%d",&op);
101 if (op==1){
102 scanf("%d%d",&a,&b);
103 pos=b/30;loc=b%30;
104 if (a>0){
105 inc((a<<loc)&inf,pos);
106 inc(a>>30-loc,pos+1);
107 } else {
108 a=-a;
109 dec((a<<loc)&inf,pos);
110 dec(a>>30-loc,pos+1);
111 }
112 } else {
113 scanf("%d",&x);
114 res=query_ans(1,0,m,x/30);
115 printf("%d
",res&(1<<x%30)&&1);
116 }
117 }
118}
119signed main(){
120 read();
121 solve();
122 return 0;
123}