Deep learning：十四(Softmax Regression练习)

　　前言：

　　这篇文章主要是用来练习softmax regression在多分类器中的应用，关于该部分的理论知识已经在前面的博文中Deep learning：十三(Softmax Regression)有所介绍。本次的实验内容是参考网页：http://deeplearning.stanford.edu/wiki/index.php/Exercise:Softmax_Regression。主要完成的是手写数字识别，采用的是MNIST手写数字数据库，其中训练样本有6万个，测试样本有1万个，且数字是0~9这10个。每个样本是一张小图片，大小为28*28的。

　　实验环境：matlab2012a

　　实验基础：

　　这次实验只用了softmax模型，也就是说没有隐含层，而只有输入层和输出层，因为实验中并没有提取出MINST样本的特征，而是直接用的原始像素特征。实验中主要是计算系统的损失函数和其偏导数，其计算公式如下所示：

 　　

　　

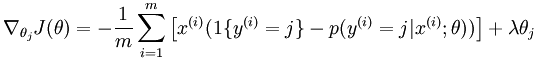
　　一些matlab函数：

　　sparse:

　　生成一个稀疏矩阵，比如说sparse(A, B, k)，，其中A和B是个向量，k是个常量。这里生成的稀疏矩阵的值都为参数k，稀疏矩阵位置值坐标点有A和B相应的位置点值构成。

　　full:

　　生成一个正常矩阵，一般都是利用稀疏矩阵来还原的。

　　实验错误：

　　按照作者给的starter code，结果连数据都加载不下来，出现如下错误提示：Error using permute Out of memory. Type HELP MEMORY for your options. 结果跟踪定位到loadMNISTImages.m文件中的images = permute(images,[2 1 3])这句代码，究其原因就是说images矩阵过大，在有限内存下不能够将其进行维度旋转变换。可是这个数据已经很小了，才几十兆而已，参考了很多out of memory的方法都不管用，后面直接把改句的前面一句代码images = reshape(images, numCols, numRows, numImages);改成images = reshape(images, numRows, numCols, numImages);反正实现的效果都是一样的。因为原因是内存问题，所以要么用64bit的matlab，要买自己对该函数去优化下，节省运行过程中的内存。

　　实验结果：

　　Accuracy: 92.640%

　　和网页教程中给的结果非常相近了。

　　实验主要部分代码：

　　softmaxExercise.m:

%% CS294A/CS294W Softmax Exercise 

%  Instructions
%  ------------
% 
%  This file contains code that helps you get started on the
%  softmax exercise. You will need to write the softmax cost function 
%  in softmaxCost.m and the softmax prediction function in softmaxPred.m. 
%  For this exercise, you will not need to change any code in this file,
%  or any other files other than those mentioned above.
%  (However, you may be required to do so in later exercises)

%%======================================================================
%% STEP 0: Initialise constants and parameters
%
%  Here we define and initialise some constants which allow your code
%  to be used more generally on any arbitrary input. 
%  We also initialise some parameters used for tuning the model.

inputSize = 28 * 28; % Size of input vector (MNIST images are 28x28)
numClasses = 10;     % Number of classes (MNIST images fall into 10 classes)

lambda = 1e-4; % Weight decay parameter

%%======================================================================
%% STEP 1: Load data
%
%  In this section, we load the input and output data.
%  For softmax regression on MNIST pixels, 
%  the input data is the images, and 
%  the output data is the labels.
%

% Change the filenames if you've saved the files under different names
% On some platforms, the files might be saved as 
% train-images.idx3-ubyte / train-labels.idx1-ubyte

images = loadMNISTImages('train-images.idx3-ubyte');
labels = loadMNISTLabels('train-labels.idx1-ubyte');
labels(labels==0) = 10; % Remap 0 to 10

inputData = images;

% For debugging purposes, you may wish to reduce the size of the input data
% in order to speed up gradient checking. 
% Here, we create synthetic dataset using random data for testing

% DEBUG = true; % Set DEBUG to true when debugging.
DEBUG = false;
if DEBUG
    inputSize = 8;
    inputData = randn(8, 100);
    labels = randi(10, 100, 1);
end

% Randomly initialise theta
theta = 0.005 * randn(numClasses * inputSize, 1);%输入的是一个列向量

%%======================================================================
%% STEP 2: Implement softmaxCost
%
%  Implement softmaxCost in softmaxCost.m. 

[cost, grad] = softmaxCost(theta, numClasses, inputSize, lambda, inputData, labels);
                                     
%%======================================================================
%% STEP 3: Gradient checking
%
%  As with any learning algorithm, you should always check that your
%  gradients are correct before learning the parameters.
% 

if DEBUG
    numGrad = computeNumericalGradient( @(x) softmaxCost(x, numClasses, ...
                                    inputSize, lambda, inputData, labels), theta);

    % Use this to visually compare the gradients side by side
    disp([numGrad grad]); 

    % Compare numerically computed gradients with those computed analytically
    diff = norm(numGrad-grad)/norm(numGrad+grad);
    disp(diff); 
    % The difference should be small. 
    % In our implementation, these values are usually less than 1e-7.

    % When your gradients are correct, congratulations!
end

%%======================================================================
%% STEP 4: Learning parameters
%
%  Once you have verified that your gradients are correct, 
%  you can start training your softmax regression code using softmaxTrain
%  (which uses minFunc).

options.maxIter = 100;
%softmaxModel其实只是一个结构体，里面包含了学习到的最优参数以及输入尺寸大小和类别个数信息
softmaxModel = softmaxTrain(inputSize, numClasses, lambda, ...
                            inputData, labels, options);
                          
% Although we only use 100 iterations here to train a classifier for the 
% MNIST data set, in practice, training for more iterations is usually
% beneficial.

%%======================================================================
%% STEP 5: Testing
%
%  You should now test your model against the test images.
%  To do this, you will first need to write softmaxPredict
%  (in softmaxPredict.m), which should return predictions
%  given a softmax model and the input data.

images = loadMNISTImages('t10k-images.idx3-ubyte');
labels = loadMNISTLabels('t10k-labels.idx1-ubyte');
labels(labels==0) = 10; % Remap 0 to 10

inputData = images;
size(softmaxModel.optTheta)
size(inputData)

% You will have to implement softmaxPredict in softmaxPredict.m
[pred] = softmaxPredict(softmaxModel, inputData);

acc = mean(labels(:) == pred(:));
fprintf('Accuracy: %0.3f%%\n', acc * 100);

% Accuracy is the proportion of correctly classified images
% After 100 iterations, the results for our implementation were:
%
% Accuracy: 92.200%
%
% If your values are too low (accuracy less than 0.91), you should check 
% your code for errors, and make sure you are training on the 
% entire data set of 60000 28x28 training images 
% (unless you modified the loading code, this should be the case)

　　softmaxCost.m

function [cost, grad] = softmaxCost(theta, numClasses, inputSize, lambda, data, labels)

% numClasses - the number of classes 
% inputSize - the size N of the input vector
% lambda - weight decay parameter
% data - the N x M input matrix, where each column data(:, i) corresponds to
%        a single test set
% labels - an M x 1 matrix containing the labels corresponding for the input data
%

% Unroll the parameters from theta
theta = reshape(theta, numClasses, inputSize);%将输入的参数列向量变成一个矩阵

numCases = size(data, 2);%输入样本的个数
groundTruth = full(sparse(labels, 1:numCases, 1));%这里sparse是生成一个稀疏矩阵，该矩阵中的值都是第三个值1
                                                    %稀疏矩阵的小标由labels和1:numCases对应值构成
cost = 0;

thetagrad = zeros(numClasses, inputSize);

%% ---------- YOUR CODE HERE --------------------------------------
%  Instructions: Compute the cost and gradient for softmax regression.
%                You need to compute thetagrad and cost.
%                The groundTruth matrix might come in handy.

M = bsxfun(@minus,theta*data,max(theta*data, [], 1));
M = exp(M);
p = bsxfun(@rdivide, M, sum(M));
cost = -1/numCases * groundTruth(:)' * log(p(:)) + lambda/2 * sum(theta(:) .^ 2);
thetagrad = -1/numCases * (groundTruth - p) * data' + lambda * theta;



% ------------------------------------------------------------------
% Unroll the gradient matrices into a vector for minFunc
grad = [thetagrad(:)];
end

　　softmaxTrain.m:

function [softmaxModel] = softmaxTrain(inputSize, numClasses, lambda, inputData, labels, options)
%softmaxTrain Train a softmax model with the given parameters on the given
% data. Returns softmaxOptTheta, a vector containing the trained parameters
% for the model.
%
% inputSize: the size of an input vector x^(i)
% numClasses: the number of classes 
% lambda: weight decay parameter
% inputData: an N by M matrix containing the input data, such that
%            inputData(:, c) is the cth input
% labels: M by 1 matrix containing the class labels for the
%            corresponding inputs. labels(c) is the class label for
%            the cth input
% options (optional): options
%   options.maxIter: number of iterations to train for

if ~exist('options', 'var')
    options = struct;
end

if ~isfield(options, 'maxIter')
    options.maxIter = 400;
end

% initialize parameters
theta = 0.005 * randn(numClasses * inputSize, 1);

% Use minFunc to minimize the function
addpath minFunc/
options.Method = 'lbfgs'; % Here, we use L-BFGS to optimize our cost
                          % function. Generally, for minFunc to work, you
                          % need a function pointer with two outputs: the
                          % function value and the gradient. In our problem,
                          % softmaxCost.m satisfies this.
minFuncOptions.display = 'on';

[softmaxOptTheta, cost] = minFunc( @(p) softmaxCost(p, ...
                                   numClasses, inputSize, lambda, ...
                                   inputData, labels), ...                                   
                              theta, options);

% Fold softmaxOptTheta into a nicer format
softmaxModel.optTheta = reshape(softmaxOptTheta, numClasses, inputSize);
softmaxModel.inputSize = inputSize;
softmaxModel.numClasses = numClasses;
                          
end                          

　　softmaxPredict.m:

function [pred] = softmaxPredict(softmaxModel, data)

% softmaxModel - model trained using softmaxTrain
% data - the N x M input matrix, where each column data(:, i) corresponds to
%        a single test set
%
% Your code should produce the prediction matrix 
% pred, where pred(i) is argmax_c P(y(c) | x(i)).
 
% Unroll the parameters from theta
theta = softmaxModel.optTheta;  % this provides a numClasses x inputSize matrix
pred = zeros(1, size(data, 2));

%% ---------- YOUR CODE HERE --------------------------------------
%  Instructions: Compute pred using theta assuming that the labels start 
%                from 1.


[nop, pred] = max(theta * data);
%  pred= max(peed_temp);


% ---------------------------------------------------------------------

end

　　参考资料：

     Deep learning：十三(Softmax Regression)

     http://deeplearning.stanford.edu/wiki/index.php/Exercise:Softmax_Regression