前言:
本节主要是来简单介绍下stacked CNN(深度卷积网络),起源于本人在构建SAE网络时的一点困惑:见Deep learning:三十六(关于构建深度卷积SAE网络的一点困惑)。因为有时候针对大图片进行recognition时,需要用到无监督学习的方法去pre-training(预训练)stacked CNN的每层网络,然后用BP算法对整个网络进行fine-tuning(微调),并且上一层的输出作为下一层的输入。这几句话说起来很简单,可是真的这么容易吗?对于初学者来说,在实际实现这个流程时并不是那么顺利,因为这其中要涉及到很多细节问题。这里不打算细讲deep statcked网络以及covolution,pooling,这几部分的内容可以参考前面的博文:Deep learning:十六(deep networks),Deep learning:十七(Linear Decoders,Convolution和Pooling)。而只只重点介绍以下一个方面的内容(具体见后面的解释)。
基础知识:
首先需要知道的是,convolution和pooling的优势为使网络结构中所需学习到的参数个数变得更少,并且学习到的特征具有一些不变性,比如说平移,旋转不变性。以2维图像提取为例,学习的参数个数变少是因为不需要用整张图片的像素来输入到网络,而只需学习其中一部分patch。而不变的特性则是由于采用了mean-pooling或者max-pooling等方法。
以经典的LeNet5结构图为例:
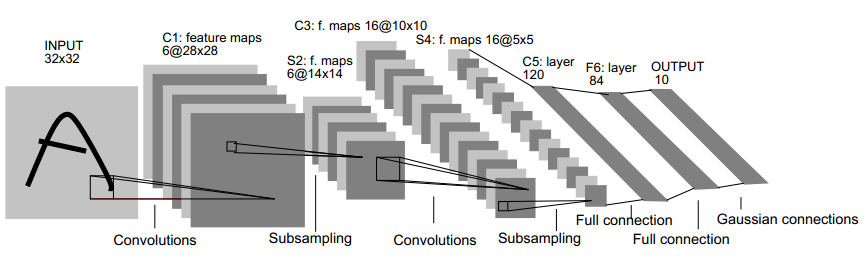
可以看出对于这个网络,每输入一张32*32大小的图片,就输出一个84维的向量,这个向量即我们提取出的特征向量。
网络的C1层是由6张28*28大小的特征图构成,其来源是我们用6个5*5大小的patch对32*32大小的输入图进行convolution得到,28=32-5+1,其中每次移动步伐为1个像素。 而到了s2层则变成了6张14*14大小的特征图,原因是每次对4个像素(即2*2的)进行pooling得到1个值。这些都很容易理解,在ufldl教程Feature extraction using convolution,Pooling中给出了详细的解释。
最难问题的就是:C3那16张10*10大小的特征图是怎么来?这才是本文中最想讲清楚的。
有人可能会讲,这不是很简单么,将S2层的内容输入到一个输入层为5*5,隐含层为16的网络即可。其实这种解释是错的,还是没有说到问题本质。我的答案是:将S2的特征图用1个输入层为150(=5*5*6,不是5*5)个节点,输出层为16个节点的网络进行convolution。
并且此时, C3层的每个特征图并不一定是都与S2层的特征图相连接,有可能只与其中的某几个连接,比如说在LeNet5中,其连接情况如下所示:
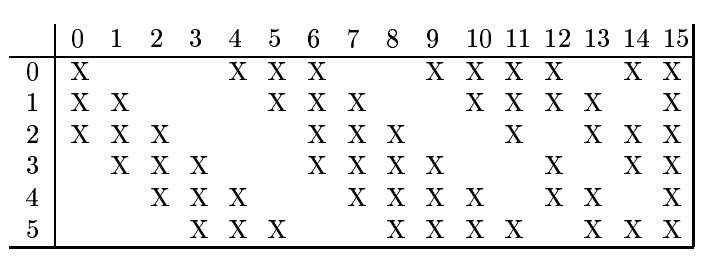
其中打X了的表示两者之间有连接的。取我们学习到的网络(结构为150-16)中16个隐含节点种的一个拿来分析,比如拿C3中的第3号特征图来说,它与上层网络S2第3,4,5号特征图连接。那么该第3号特征图的值(假设为H3)是怎么得到的呢?其过程如下:
首先我们把网络150-16(以后这样表示,表面输入层节点为150,隐含层节点为16)中输入的150个节点分成6个部分,每个部分为连续的25个节点。取出倒数第3个部分的节点(为25个),且同时是与隐含层16个节点中的第4(因为对应的是3号,从0开始计数的)个相连的那25个值,reshape为5*5大小,用这个5*5大小的特征patch去convolution S2网络中的倒数第3个特征图,假设得到的结果特征图为h1。
同理,取出网络150-16中输入的倒数第2个部分的节点(为25个),且同时是与隐含层16个节点中的第5个相连的那25个值,reshape为5*5大小,用这个5*5大小的特征patch去convolution S2网络中的倒数第2个特征图,假设得到的结果特征图为h2。
继续,取出网络150-16中输入的最后1个部分的节点(为25个),且同时是与隐含层16个节点中的第5个相连的那25个值,reshape为5*5大小,用这个5*5大小的特征patch去convolution S2网络中的最后1个特征图,假设得到的结果特征图为h3。
最后将h1,h2,h3这3个矩阵相加得到新矩阵h,并且对h中每个元素加上一个偏移量b,且通过sigmoid的激发函数,即可得到我们要的特征图H3了。
终于把想要讲的讲完了,LeNet5后面的结构可以类似的去推理。其实发现用文字去描述这个过程好难,如果是面对面交谈的话,几句话就可以搞定。
因为在经典的CNN网络结构中(比如这里的LeNet5),是不需要对每层进行pre-traing的。但是在目前的stacked CNN中,为了加快最终网络参数寻优的速度,一般都需要用无监督的方法进行预训练。现在来解决在Deep learning:三十六(关于构建深度卷积SAE网络的一点困惑)中的第1个问题,对应到LeNet5框架中该问题为:pre-training从S2到C3的那个150-16网络权值W时,训练样本从哪里来?
首先,假设我们总共有m张大图片作为训练样本,则S2中共得到6*m张特征图,其大小都是14*14,而我们对其进行convolution时使用的5*5大小的,且我们输入到该网络是150维的,所以肯定需要对这些数据进行sub-sample。因此我们只需对这6*m张图片进行采样,每6张特征图(S2层的那6张)同时随机采样若干个5*5大小(即它们每个的采样位置是一样的)的patch, 并将其按照顺序res为hape150维,此作为150-16网络的一个训练样本,用同样的方法获取多个样本,共同构成该网络的训练样本。
这里给出这几天在网上搜的一些资料:
首先是LeNet5对应的手写字体识别的demo,可以参考其网页:LeNet-5, convolutional neural networks,以及该demo对应的paper:LeCun, Y., et al. (1998). "Gradient-based learning applied to document recognition.",这篇paper内容比较多,只需看其中的单个文字识别那部分。paper中关于LeNet5各层网络的详细内容可以参考网页:Deep Learning(深度学习)学习笔记整理系列之(七).
下面这个是用python写的一个简单版本的LeNet5,用Theano机器学习库实现的:Convolutional Neural Networks (LeNet),懂Python的同学可以看下,比较通俗易懂(不懂Python其实也能看懂个大概)。关于stacked CNN的matlab实现可以参考:https://sites.google.com/site/chumerin/projects/mycnn。里面有源码和界面。
最后Hition在2012年ImageNet识别时用的算法paper:Imagenet classification with deep convolutional neural networks. 他还给出了对应的code,基于GPU,c++的:https://code.google.com/p/cuda-convnet/。
总结:
关于Statcked CNN网络pre-training过程中,后续层的训练样本来源已经弄清楚了,但是关于最后对整个网络的fine-tuning过程还不是很明白,里面估计有不少数学公式。
参考资料:
Deep learning:三十六(关于构建深度卷积SAE网络的一点困惑)
Deep learning:十六(deep networks)
Deep learning:十七(Linear Decoders,Convolution和Pooling)
Deep Learning(深度学习)学习笔记整理系列之(七)
Convolutional Neural Networks (LeNet)
https://sites.google.com/site/chumerin/projects/mycnn.
Gradient-based learning applied to document recognition.
Imagenet classification with deep convolutional neural networks.
Feature extraction using convolution