吴裕雄--天生自然数据结构学习笔记：图的邻接表存储结构详解

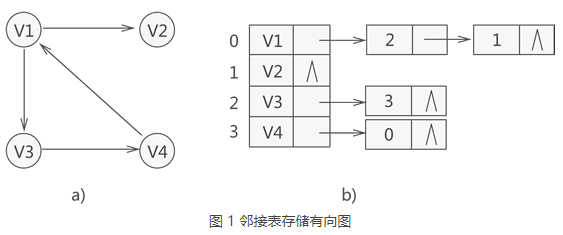
通常，图更多的是采用链表存储，具体的存储方法有 3 种，分别是邻接表、邻接多重表和十字链表。

本节先讲解图的邻接表存储法。邻接表既适用于存储无向图，也适用于存储有向图。

在具体讲解邻接表存储图的实现方法之前，先普及一个"邻接点"的概念。在图中，如果两个点相互连通，即通过其中一个顶点，可直接找到另一个顶点，则称它们互为邻接点。
邻接指的是图中顶点之间有边或者弧的存在。

邻接表存储图的实现方式是，给图中的各个顶点独自建立一个链表，用节点存储该顶点，用链表中其他节点存储各自的临界点。

与此同时，为了便于管理这些链表，通常会将所有链表的头节点存储到数组中（也可以用链表存储）。也正因为各个链表的头节点存储的是各个顶点，因此各链表在存储临界点数据时，仅需存储该邻接顶点位于数组中的位置下标即可。

例如，存储图 1a) 所示的有向图，其对应的邻接表如图 1b) 所示：

 

#define  MAX_VERTEX_NUM 20//最大顶点个数
#define  VertexType int//顶点数据的类型
#define  InfoType int//图中弧或者边包含的信息的类型
typedef struct ArcNode{
    int adjvex;//邻接点在数组中的位置下标
    struct ArcNode * nextarc;//指向下一个邻接点的指针
    InfoType * info;//信息域
}ArcNode;
typedef struct VNode{
    VertexType data;//顶点的数据域
    ArcNode * firstarc;//指向邻接点的指针
}VNode,AdjList[MAX_VERTEX_NUM];//存储各链表头结点的数组
typedef struct {
    AdjList vertices;//图中顶点的数组
    int vexnum,arcnum;//记录图中顶点数和边或弧数
    int kind;//记录图的种类
}ALGraph;

邻接表计算顶点的出度和入度
使用邻接表计算无向图中顶点的入度和出度会非常简单，只需从数组中找到该顶点然后统计此链表中节点的数量即可。

而使用邻接表存储有向图时，通常各个顶点的链表中存储的都是以该顶点为弧尾的邻接点，因此通过统计各顶点链表中的节点数量，只能计算出该顶点的出度，而无法计算该顶点的入度。

对于利用邻接表求某顶点的入度，有两种方式：
遍历整个邻接表中的节点，统计数据域与该顶点所在数组位置下标相同的节点数量，即为该顶点的入度；
建立一个逆邻接表，该表中的各顶点链表专门用于存储以此顶点为弧头的所有顶点在数组中的位置下标。比如说，建立一张图 1a) 对应的逆邻接表，如图 4 所示：

对于具有 n 个顶点和 e 条边的无向图，邻接表中需要存储 n 个头结点和 2e 个表结点。在图中边或者弧稀疏的时候，使用邻接表要比前一节介绍的邻接矩阵更加节省空间。