最长公共子序列（动态规划）

求两个字符串的最长公共子序列

创建dp数组

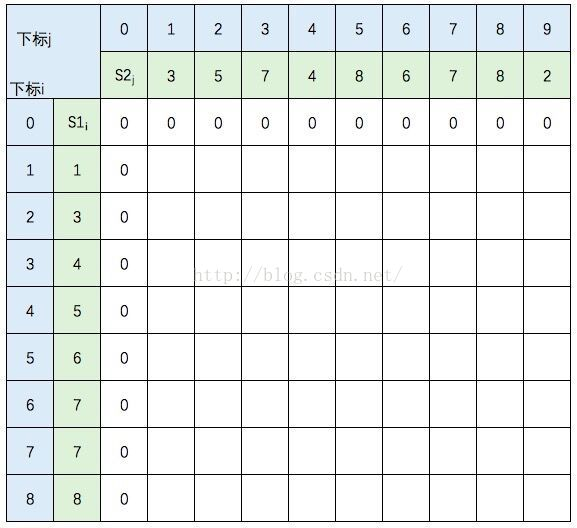
边界条件如图所示，dp[i][0] = dp[0][j] = 0

之后根据状态转移方程求出整个二维数组的值

①当A[i] == B[j]  时，则字符串A和字符串B的最长公共子序列增加了一位，即dp[i][j] = dp[i-1][j-1] + 1;

②当A[i] != B[i] 时，则字符串A和字符串B的最长公共子序列无法延长，则继承 dp[i-1][j] 和 dp[i][j-1] 中最大的一位

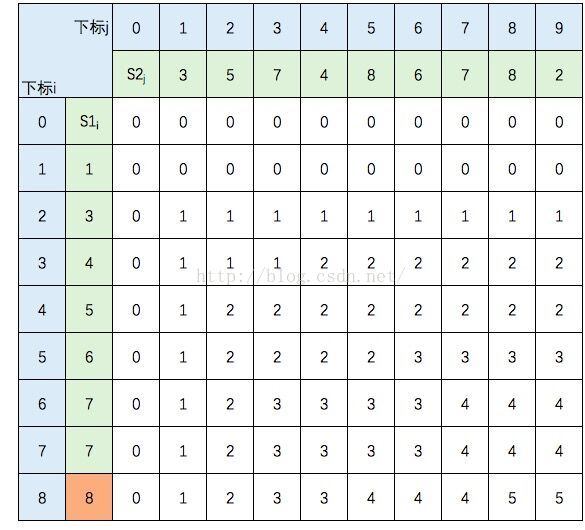
最终填充完毕

#include<iostream>
#include<string>
using namespace std;
//const int maxn = 1000;
int main()
{
    string str1;
    string str2;
    int dp[100][100] = {0};
    while(cin>>str1>>str2)
    {
        int len1 = str1.length();
        int len2 = str2.length();
        //初始化边界条件
        for(int i=0;i<=len1;i++)
            dp[i][0] = 0;
        for(int j=0;j<=len2;j++)
            dp[0][j] = 0;
        //利用状态转移方程计算dp,
        for(int i = 1;i<=len1;i++)
        {
            for(int j=1;j<=len2;j++)
            {
                if(str1[i-1] == str2[j-1])
                    dp[i][j] = dp[i-1][j-1] + 1;
                else
                    dp[i][j] = max(dp[i][j-1],dp[i-1][j]);
            }
        }
        cout<<dp[len1][len2]<<endl;
    }
    return 0;
}

 参考博客：https://blog.csdn.net/someone_and_anyone/article/details/81044153