这个题弄得我怀疑人生,读题就走了半天弯路
一开始半天都没搞清楚,原来是 让我连续地分段,不必打乱重排,故想办法找到分段的端点值即可
在每次找到一个端点值之后,与下次的衔接稍微麻烦
剩下的就是愉快的倍增了
算法回顾:
题目给出固定的数列a,要求将数列a分段,要求每一段的“校验值”要<=k。
“校验值”求法:从你分的段中取出m对数,求每对数差的平方之和的最大值 (设Di为每对数的差 ,“校验值”:SPD=∑Di^2最大)
求得“校验值”的方法可用贪心,将a1~an 排序,让最大和最小,次大和次小这样地取出来,然后直接就是最大值
这个贪心的正确性可以证明,我们用反证的方法
设a为排好序的数列,设S1用取头尾的方法,S2用取最大和次小,最小和次大的方法
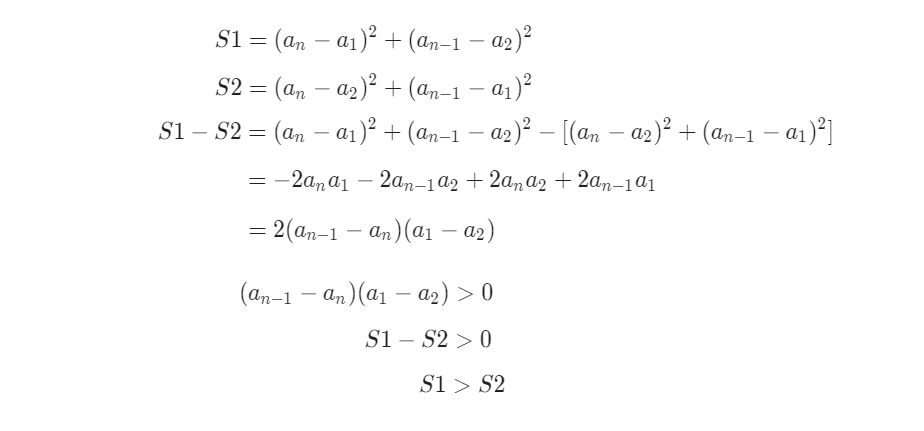
故用取头尾的方法更优
为了尽量分组最少,我们还需要用优化的方法找分组断点,这里可以想到二分、倍增。
一开始想到二分,然而显然不是最优,而且还改了半天
40分二分代码:

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<cmath> 5 #include<algorithm> 6 #define llint long long 7 #define pau system("pause") 8 using namespace std; 9 int t; 10 int n,m,k; 11 int a[500005]; 12 int tmp[52000]; 13 inline bool check(int l,int r) 14 { 15 llint sum=0; 16 int f=0; 17 for(int i=l;i<=r;i++) tmp[++f]=a[i];//将原来的复制过来排序一次 18 stable_sort(tmp+1,tmp+1+f); 19 for(int i=1;i<=min(m,(r-l+1)/2);i++) 20 { 21 int s1=tmp[i]-tmp[f-i+1]; 22 sum+=s1*s1; 23 } 24 if(l==r) sum=0; 25 if(sum<=k) return true; 26 else return false; 27 } 28 int main() 29 { 30 scanf("%d",&t); 31 while(t--) 32 { 33 scanf("%d%d%d",&n,&m,&k); 34 for(int i=1;i<=n;i++) 35 { 36 scanf("%d",&a[i]); 37 } 38 //二分出一个端点值使得左半边spd合法且尽量长 39 int L=1;//未解决区间的左端点值 40 int cnt=0,rpoint=1; 41 while(L<=n)//注意这里进入下一段未解决区间,L值要到这个r的右边一个 42 { 43 int l=L,r=n; 44 rpoint=L;//防止找不到r 45 while(l<=r)//用二分法求下一次的右端点 46 { 47 int mid = (l+r)>>1; 48 if(check(L,mid)) rpoint = mid, l = mid+1;//扩大合法答案 49 else r = mid-1; 50 } 51 L = rpoint+1; 52 cnt++; 53 } 54 cout<<cnt<<endl; 55 } 56 }
然而这道题的特征显然不是二分
我们可以设计一种更有目的性的解法,每次向右找一个尽量远的端点值:倍增
而且,光有倍增是不行的,由于重复排序我们每次又浪费大量的时间,所以我们想到了归并排序
为了卡常数,读优写优都上了

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #include<cmath> 5 #include<algorithm> 6 #define llint long long 7 #define re register 8 #define pau system("pause") 9 using namespace std; 10 template <typename ty> inline void read(ty &x) 11 { 12 x=0;int f=1;re char c=getchar(); 13 for(;c<'0'||c>'9';c=getchar()) if(c=='-') f=-1; 14 for(;c>='0'&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48); 15 x*=f; 16 } 17 template <typename ty> inline void write(ty x) 18 { 19 if(x<0) putchar('-'),x=-x; 20 if(x>9) write(x/10); 21 putchar(x%10+48); 22 } 23 int t; 24 int n,m; 25 llint k; 26 llint a[500005]; 27 llint s[500005],s2[500005];//为了用归并思想提速 s为常有序数列, s2用来试探答案 28 inline void resort(int l,int rp,int r) 29 { 30 for(re int i=rp+1;i<=r;i++) s[i]=a[i];//将原来的复制过来排序一次 31 stable_sort(s+rp+1,s+r+1); 32 merge(s+l,s+rp+1,s+rp+1,s+r+1,s2+l); 33 } 34 inline bool check(int l,int rp,int r)//rp为原来的r,r为增加了len的r 35 { 36 llint sum=0; 37 resort(l,rp,r);//归并提速 38 for(re int i=1;i<=min(m,(r-l+1)/2);i++)//注意这里一定要加min(m,(r-l+1)/2),因为可能m个不够取 39 { 40 llint s1 = s2[l+i-1]-s2[r-i+1]; 41 sum += s1*s1; 42 if(sum>k) return false;//魔鬼般的剪枝,可以多对一个点 43 } 44 45 if(l==r) sum=0; 46 if(sum<=k) 47 { 48 for(re int i=l;i<=r;i++) s[i]=s2[i];//此处的r已被认可,下次传来的r一定在右边,故排好序的数列可以保存 49 return true; 50 } 51 else return false; 52 } 53 54 int main() 55 { 56 // freopen("input2","r",stdin); 57 read(t); 58 while(t--) 59 { 60 read(n),read(m),read(k); 61 for(re int i=1;i<=n;i++) 62 { 63 read(a[i]); 64 } 65 int l=1; 66 int cnt=0; 67 68 s[1]=a[1];//恶魔般的初始化 69 70 while(l<=n) 71 { 72 int r=l;//欲寻找的右端点值 73 int len=1; 74 while(len!=0)//通过倍增的方法找右端点 75 { 76 if(r+len<=n && check(l,r,r+len)) r+=len,len<<=1; 77 else len>>=1; 78 } 79 l=r+1;//下一次的左端点的衔接 80 cnt++; 81 } 82 write(cnt),putchar(' '); 83 } 84 }
