The King’s Ups and Downs

原文：https://blog.csdn.net/niuox/article/details/8866907

The King’s Ups and Downs

The king has guards of all different heights. Rather than line them up in increasing or decreasing height order, he wants to line them up so each guard is either shorter than the guards next to him or taller than the guards next to him (so the heights go up and down along the line). For example, seven guards of heights 160, 162, 164, 166, 168, 170 and 172 cm. could be arranged as:

or perhaps:

The king wants to know how many guards he needs so he can have a different up and down order at each changing of the guard for rest of his reign. To be able to do this, he needs to know for a given number of guards, n, how many different up and down orders there are:

For example, if there are four guards: 1, 2, 3,4 can be arrange as:
1324, 2143, 3142, 2314, 3412, 4231, 4132, 2413, 3241, 1423

For this problem, you will write a program that takes as input a positive integer n, the number of guards and returns the number of up and down orders for n guards of differing heights.
Input
The first line of input contains a single integer P, (1 <= P <= 1000), which is the number of data sets that follow. Each data set consists of single line of input containing two integers. The first integer, D is the data set number. The second integer, n (1 <= n <= 20), is the number of guards of differing heights.
Output
For each data set there is one line of output. It contains the data set number (D) followed by a single space, followed by the number of up and down orders for the n guards.
Sample Input
4
1 1
2 3
3 4
4 20
Sample Output
1 1
2 4
3 10
4 740742376475050

解题思路：
题意是求1-n 的全排列中有多少呈现高低高低高低或者地高低高形式排列的个数。

这种排列叫做：alternating permutations 或者 Extremal Permutations 。

可以用DP做。

dp(n,k)表示：长度为n，最后一个数为k，最后两个数是递增的 排列的个数;

dp2(n,k)表示：长度为n,最后一个数为k,最后两个数是递减的 排列的个数;

那么：

dp(n,k) = dp2(n,n+1-k) ;

很好理解吧，比如说132(低高低)等价于312(高低高)，相对的位置加起来等于4.

那么我们针对dp[n][k]的最后一位进行如下考虑：

最后一位是k，因为dp[n][k]最后两个数字是递增的，所以第n-1位的最大值是k-1。那么我们很容易推导出DP方程：

又：

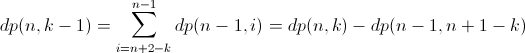
所以：dp(n,k) = dp(n-1,n+1-k) + dp(n,k-1)；

作者：niuox
来源：CSDN
原文：https://blog.csdn.net/niuox/article/details/8866907
版权声明：本文为博主原创文章，转载请附上博文链接！